Similar Polygons 7 2 Goals 1 Identify similar

Similar Polygons 7. 2

Goals 1. Identify similar polygons 2. Use similar polygons to solve problems.

Identifying Similar Polygons When two polygons have corresponding angles that are congruent and the lengths of their corresponding sides are proportional the two polygons are called similar polygons. means “is similar to” ABCD ~ EFGH

Writing Similarity Statements Pentagons JKLMN and STUVW are similar. List all the pairs of congruent angles. Write the ratios of the corresponding sides in a statement of proportionality. Because JKLMN ~ STUVW, you can write J S, K T, L U, M V, and N W. The statement of proportionality would go as follows:

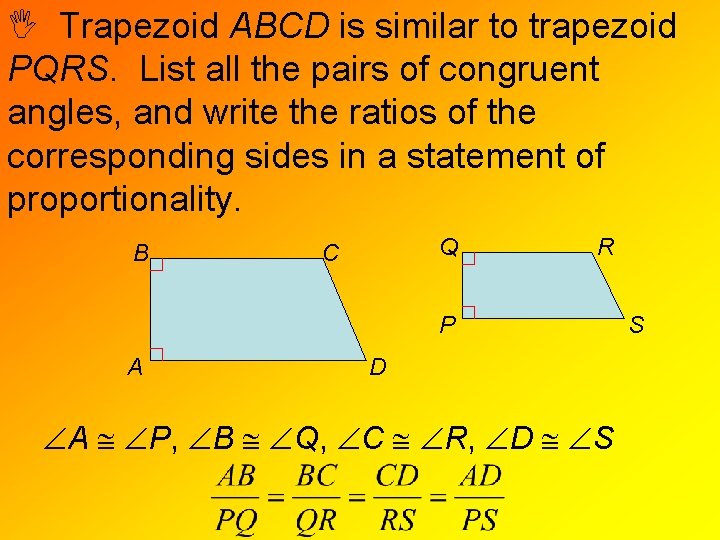
Trapezoid ABCD is similar to trapezoid PQRS. List all the pairs of congruent angles, and write the ratios of the corresponding sides in a statement of proportionality. B Q C R P A D A P, B Q, C R, D S S

Comparing Similar Polygons Decide whether the figures are similar. If they are similar, write a similarity statement. To be similar, two polygons must have congruent corresponding angles… …and proportionate corresponding sides. WXYZ ~ PQRS

Comparing Photographic Enlargements You have been asked to create a poster to advertise a field trip to see the Liberty Bell. You have a 3. 5 inch by 5 inch photo that you want to enlarge. You want the enlargement to be 16 inches wide. How long will it be? 1. Write a proportion comparing the measurements of the enlargement to the original photo 2. Solve for x The length will be about 23 inches.

Scale Factor If two polygons are similar, then the ratio of the lengths of two corresponding sides is called the scale factor. The rectangular patio around a pool is similar to the pool. Calculate the scale factor of the patio to the pool, and find the ratio of their perimeters. Since the patio and the pool are similar rectangles, the scale factor is 48 ft : 32 ft or 24 ft : 16 ft, which both simplify to 3 : 2. The perimeter of the patio is 2(24) + 2(48) = 144 feet and the perimeter of the pool is 2(16) + 2(32) = 96 feet. Therefore, the ratio of their perimeters is

Using Similar Polygons Theorem If two polygons are similar, then the ratio of their perimeters is equal to the ratios of their corresponding side lengths. Quadrilateral JKLM is similar to quadrilateral PQRS. Find the value of z. 1. Write proportion 2. Substitute given values 3. Solve for z 60 = 15 z 4=z