SIMD Parallelization of Applications that Traverse Irregular Data

SIMD Parallelization of Applications that Traverse Irregular Data Structures Bin Ren, Gagan Agrawal, James R. Larus, Todd Mytkowicz, Tomi Poutanen, Wolfram Schulte Microsoft Research，Redmond The Ohio State University 12/7/2020 1

Contributions Ø Emulate a MIMD machine in SIMD to exploit finegrained parallelism on irregular, pointer intensive data structures ü ü Tree/Graph applications that traverse many independent data structures (e. g. , regular expressions or random forests) Challenges: • • 12/7/2020 Poor Data Locality Dynamic data-driven behavior from data dependencies and control dependencies 2

Exploit SIMD Hardware? Example: Random Forests Input feature vector: <f 0 = 0. 6, f 1 = 0. 7, f 2 = 0. 2, f 3 = 0. 2> float Search(float features[]) { float feature = features[this->feature. Index]; … if (feature <= this->threshold) return this->left->Search(features); else return this->right->Search(features); … } 12/7/2020 3

Imagine a simple machine Ø Two types of opcodes Ø T ops manage control flow (e. g. , jmp, breq, …) Ø W ops manage data (e. g. , loads, stores, increment, …) Ø Map opcodes to operations on irregular data structure Ø Emulate MIMD (T & W) in SIMD Ø Each SIMD lane traverses 1 irregular data structure Ø If opcodes are simple, we see speedups! Ø Opcodes are domain specific Ø Paper describes T’s and W’s in more detail 12/7/2020 4

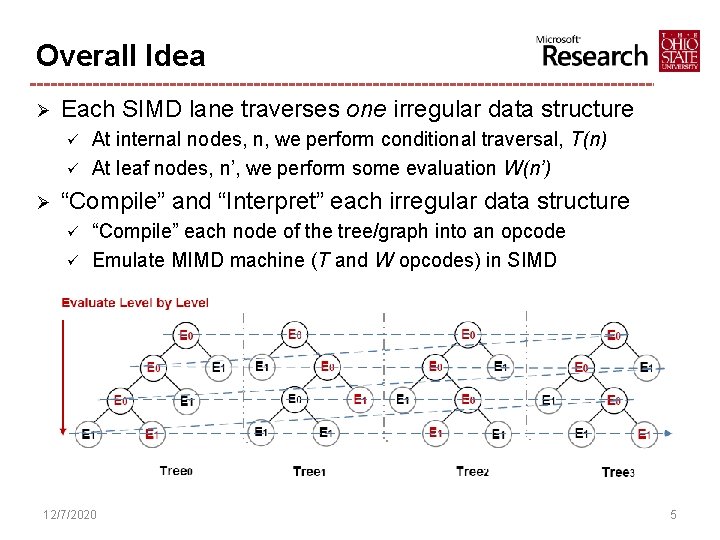
Overall Idea Ø Each SIMD lane traverses one irregular data structure ü ü Ø At internal nodes, n, we perform conditional traversal, T(n) At leaf nodes, n’, we perform some evaluation W(n’) “Compile” and “Interpret” each irregular data structure ü ü “Compile” each node of the tree/graph into an opcode Emulate MIMD machine (T and W opcodes) in SIMD 12/7/2020 5

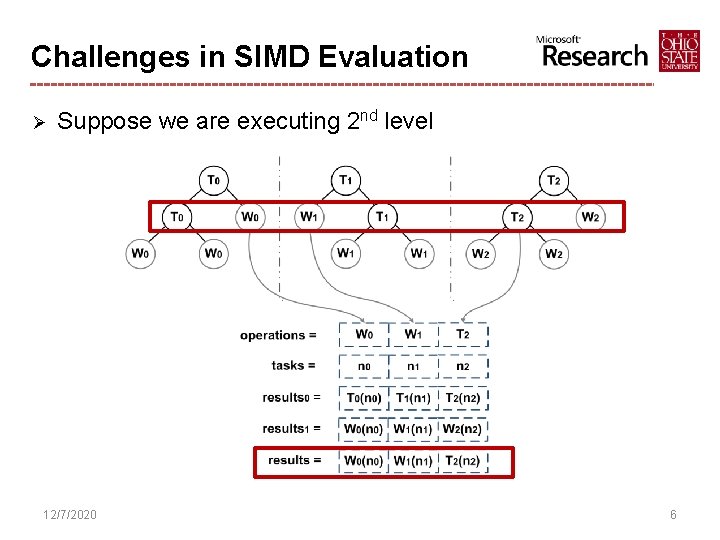
Challenges in SIMD Evaluation Ø Suppose we are executing 2 nd level 12/7/2020 6

Challenges in SIMD Evaluation Ø Branch-less Addressing of Children ü ü ü Branch operations slow SIMD Control dependence is difficult to vectorize Example: if (cond 0){ next 0 = B 0; } else {next 0 = C 0; } if (cond 1){ next 1 = B 1; } else {next 1 = C 1; } if (cond 2){ next 2 = B 2; } else {next 2 = C 2; } if (cond 3){ next 3 = B 3; } else {next 3 = C 3; } Ci = B i + 1 next 0 = C 0 – cond 0; next 1 = C 1 – cond 1; next 2 = C 2 – cond 2; next 3 = C 3 – cond 3; 12/7/2020 Vectorize by SSE __m 128 i cond = _mm_cmple_ps(…); __m 128 i next = Load (C 0, C 1, C 2, C 3); next = _mm_add_epi 32(next, cond); 7

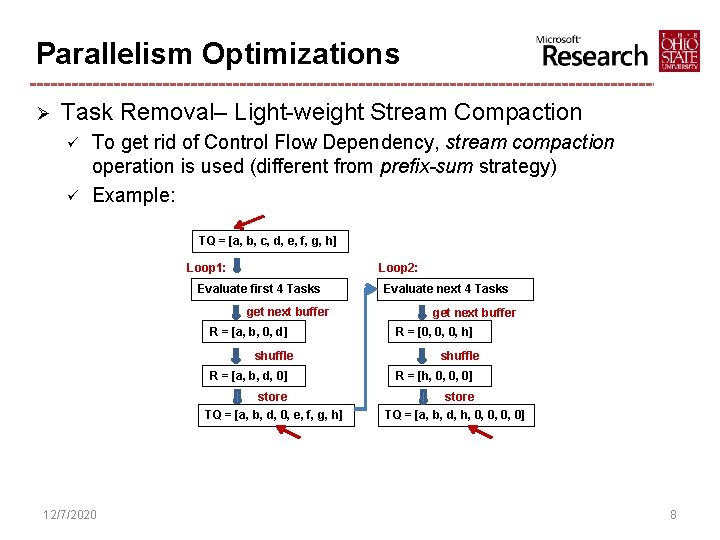
Parallelism Optimizations Ø Task Removal– Light-weight Stream Compaction ü ü To get rid of Control Flow Dependency, stream compaction operation is used (different from prefix-sum strategy) Example: TQ = [a, b, c, d, e, f, g, h] Loop 1: Loop 2: Evaluate first 4 Tasks get next buffer R = [a, b, 0, d] shuffle R = [a, b, d, 0] store TQ = [a, b, d, 0, e, f, g, h] 12/7/2020 Evaluate next 4 Tasks get next buffer R = [0, 0, 0, h] shuffle R = [h, 0, 0, 0] store TQ = [a, b, d, h, 0, 0] 8

Parallelism Optimizations Ø Stream Compaction next. Eval. Buffer[num_trees] = {H 0, {B 0, {0, B 1, 0, 0, 0, C 2, H 5, 0, 0, D 3, B 3, H 7, 0, E 4, 0, B 4, 0, D 5, 0}0, D 5, B 5, F 6, 0, 0} C 6, D 7} B 7} {D 0, E 1, F 2, E 4, F 6, {A 0, 0, H 3, A 1, A 2, A 3, A 4, A 5, A 6, A 7} 12/7/2020 9

Parallelism Optimizations Ø Data Layout ü ü ü Data locality is a key factor for parallel performance A layouts generation process to organize data in the order they are likely to be accessed Transparent to the interpreter because of the uniform interface 12/7/2020 10

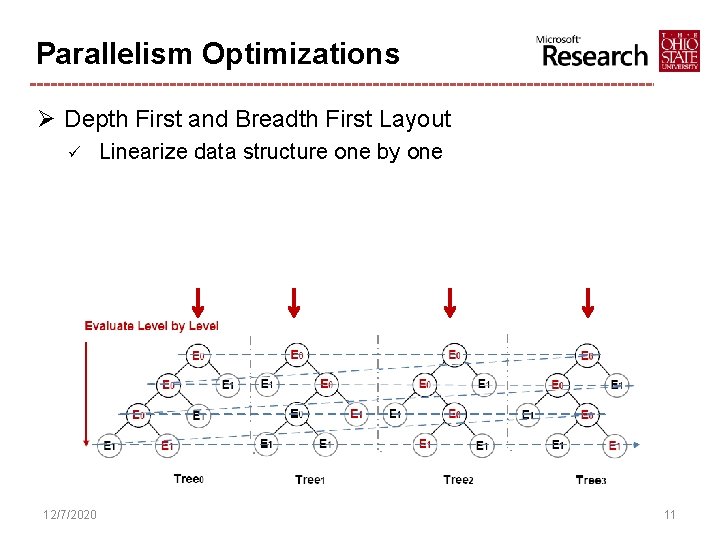
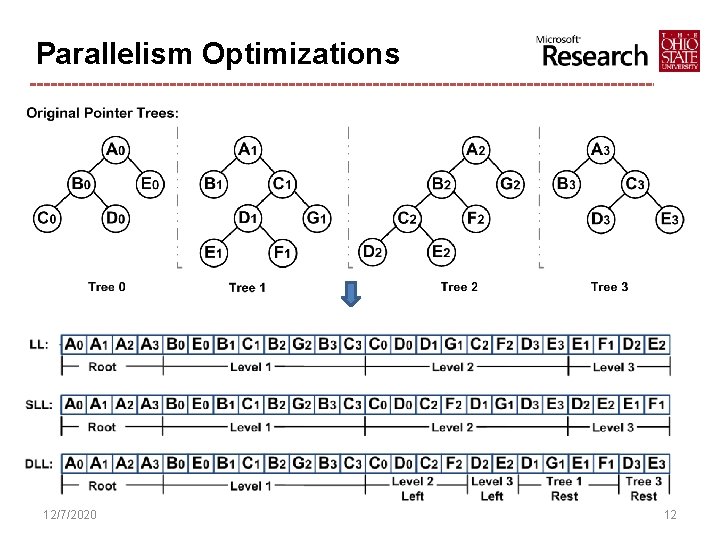
Parallelism Optimizations Ø Depth First and Breadth First Layout ü 12/7/2020 Linearize data structure one by one 11

Parallelism Optimizations 12/7/2020 12

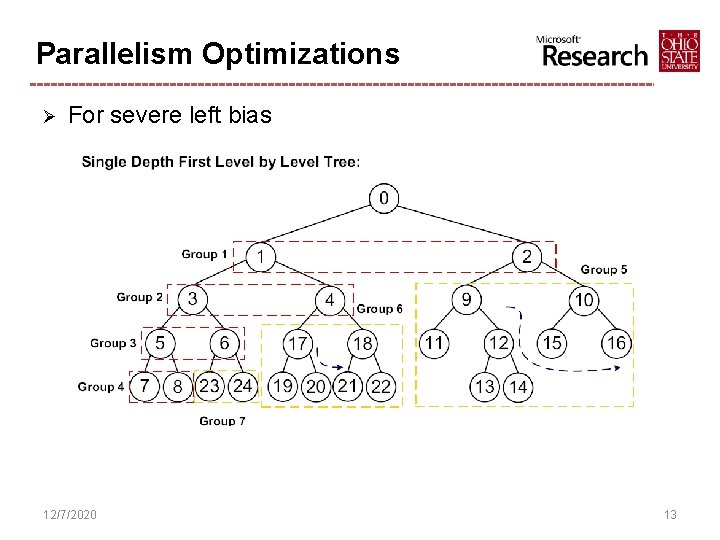
Parallelism Optimizations Ø For severe left bias 12/7/2020 13

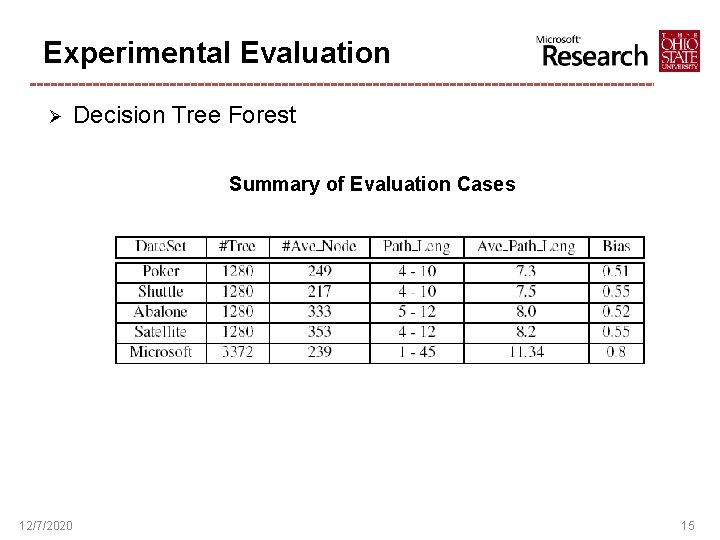
Experimental Evaluation Ø Environment ü ü Ø Intel Xeon E 5420 CPU (2. 5 GHz frequency) with SSE-4 Intel ICC compiler Applications ü Decision Tree Forest § § ü Regular Expressions § § Ø NFA based regular expression engine with O(nm) complexity Compare with GNU grep Objectives of Evaluation ü ü 12/7/2020 Built from ALGLIB and Microsoft product For ALGLIB experiments, using four data sets from UCI Machine Learning Repository – Poker, Shuttle, Abalone, and Satellite Overall Speedups from SIMD Parallelization Benefits from Optimizations 14

Experimental Evaluation Ø Decision Tree Forest Summary of Evaluation Cases 12/7/2020 15

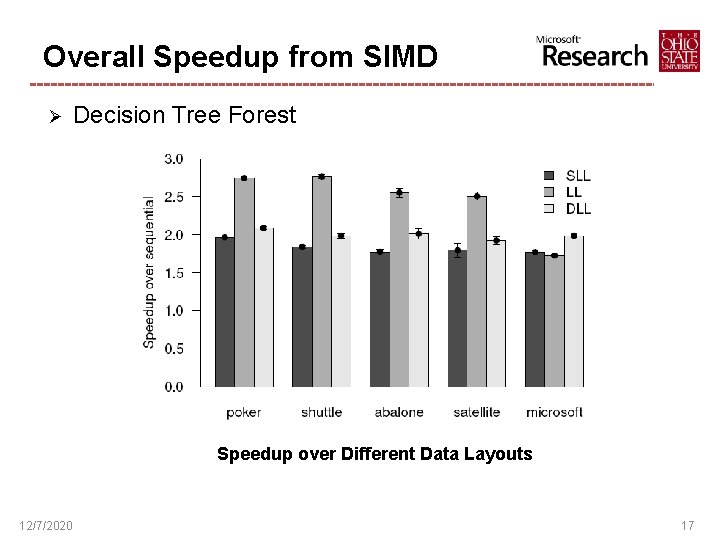
Overall Speedup from SIMD Ø Decision Tree Forest Speedup over Baseline Implementations 12/7/2020 16

Overall Speedup from SIMD Ø Decision Tree Forest Speedup over Different Data Layouts 12/7/2020 17

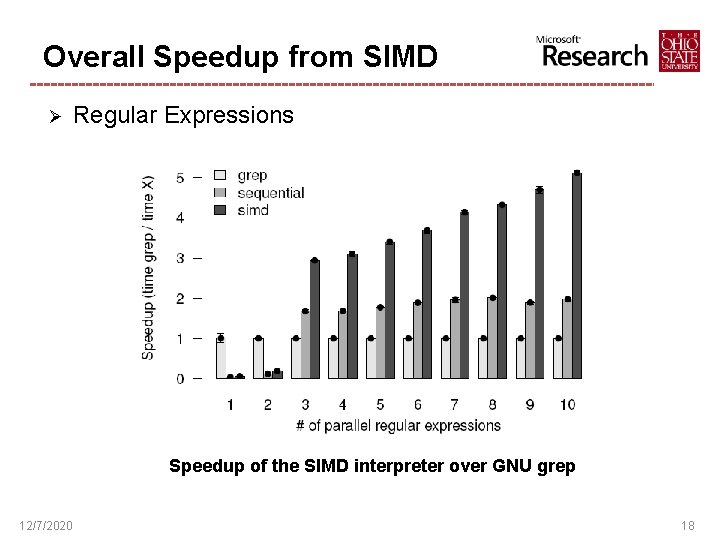
Overall Speedup from SIMD Ø Regular Expressions Speedup of the SIMD interpreter over GNU grep 12/7/2020 18

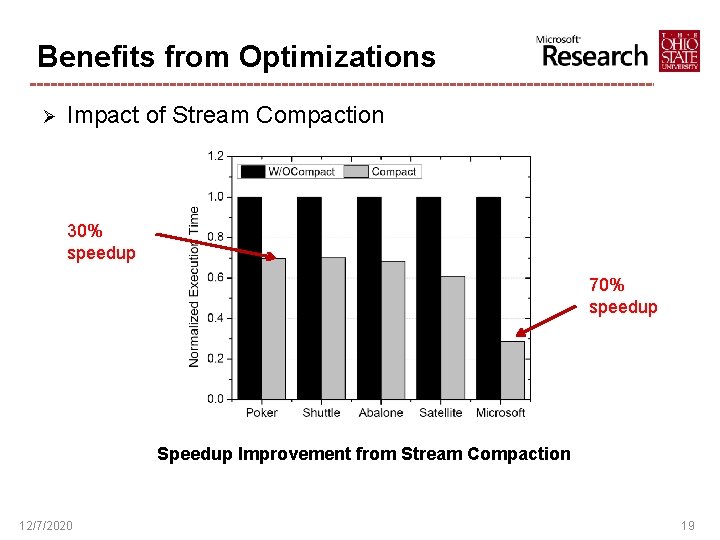
Benefits from Optimizations Ø Impact of Stream Compaction 30% speedup 70% speedup Speedup Improvement from Stream Compaction 12/7/2020 19

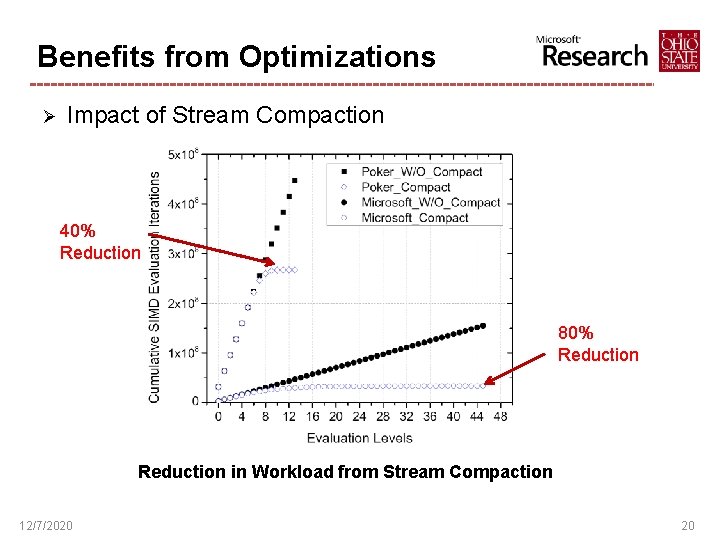
Benefits from Optimizations Ø Impact of Stream Compaction 40% Reduction 80% Reduction in Workload from Stream Compaction 12/7/2020 20

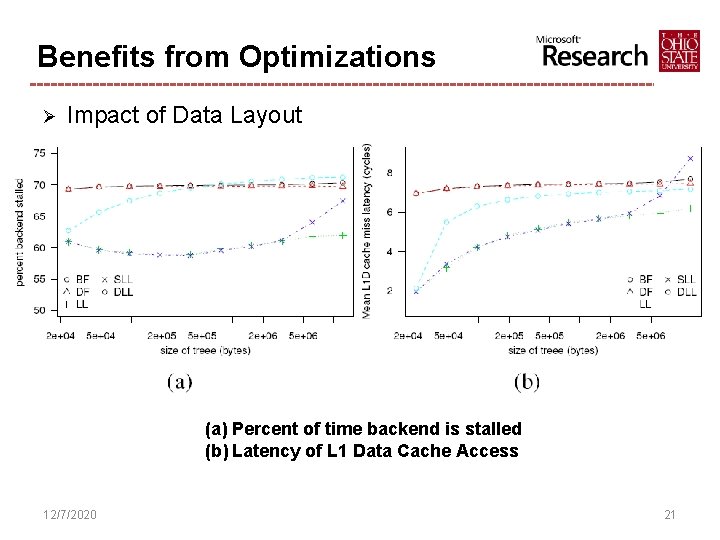
Benefits from Optimizations Ø Impact of Data Layout (a) Percent of time backend is stalled (b) Latency of L 1 Data Cache Access 12/7/2020 21

Related Work Ø Compiler-based efforts to parallelize pointer-based structures ü ü Ø M. Kulkarni, M. Burtscher, R. Inkulu, K. Pingali, and C. Casc¸aval. How Much Parallelism is There in Irregular Applications? (PPo. PP 2009) Y. Jo and M. Kulkarni. Enhancing Locality for Recursive Traversals of Recursive Structures. (OOPSLA 2011) Tree and graph traversal algorithms on SIMD architectures ü P. Harish and P. Narayanan. Accelerating Large Graph Algorithms on the GPU using CUDA. (Hi. PC 2007) ü T. Sharp. Implementing Decision Trees and Forests on a GPU. (ECCV 2008) ü C. Kim, J. Chhugani, N. Satish, E. Sedlar, A. D. Nguyen, T. Kaldewey, V. W. Lee, S. A. Brandt, and P. Dubey. FAST: Fast Architecture Sensitive Tree Search on Modern CPUs and GPUs. (SIGMOD 2010) Ø Emulating MIMD with SIMD ü G. E. Blelloch, S. Chatterjee, J. C. Hardwick, J. Sipelstein, and M. Zagha. Implementation of a Portable Nested Data-Parallel Language. (JPDC 1994) 12/7/2020 22

Conclusion Ø Approach to traverse and compute on multiple, independent, irregular data structures in parallel using SSE Ø Design multiple optimizations to exploit features found on modern hardware Ø Implement two case studies to demonstrate the utility of our approach and show significant single-core speedups 12/7/2020 23

Thanks for Your Attention! Any Questions? 12/7/2020 24

Backup Slides 12/7/2020 25

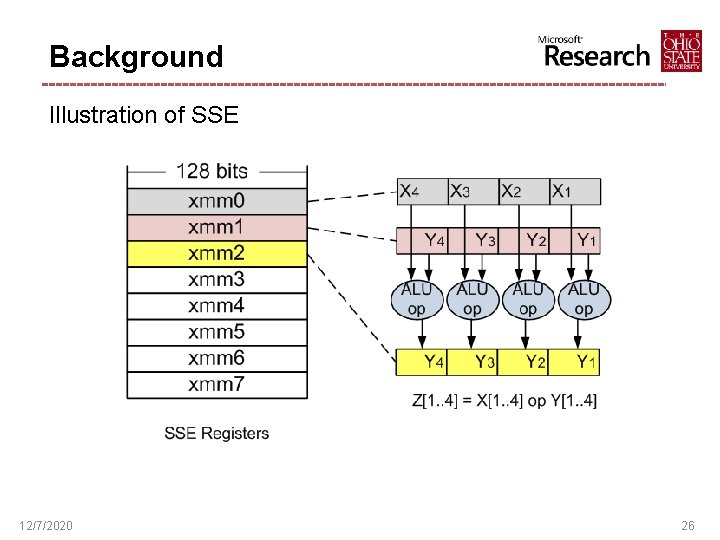
Background Illustration of SSE 12/7/2020 26

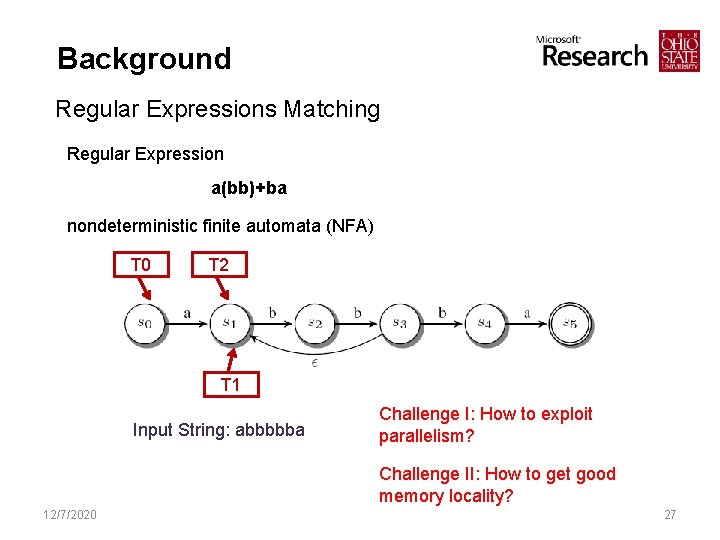
Background Regular Expressions Matching Regular Expression a(bb)+ba nondeterministic finite automata (NFA) T 0 T 2 T 1 Input String: abbbbba Challenge I: How to exploit parallelism? Challenge II: How to get good memory locality? 12/7/2020 27

Challenges in SIMD Evaluation Ø General representation of Interpreter (Tasks Scheduler) 12/7/2020 28

Challenges in SIMD Evaluation Ø An Interpreter for Random Forest Compilation: Instruction Format ü T Instruction (compare): short: 2 bytes float: 4 bytes long: 8 bytes W Instruction (output): 12/7/2020 29

Challenges in SIMD Evaluation Ø An Interpreter for Regular Expression Matching ü 12/7/2020 Compilation: Instruction Format (similar to Cox’s NFA engine) 30

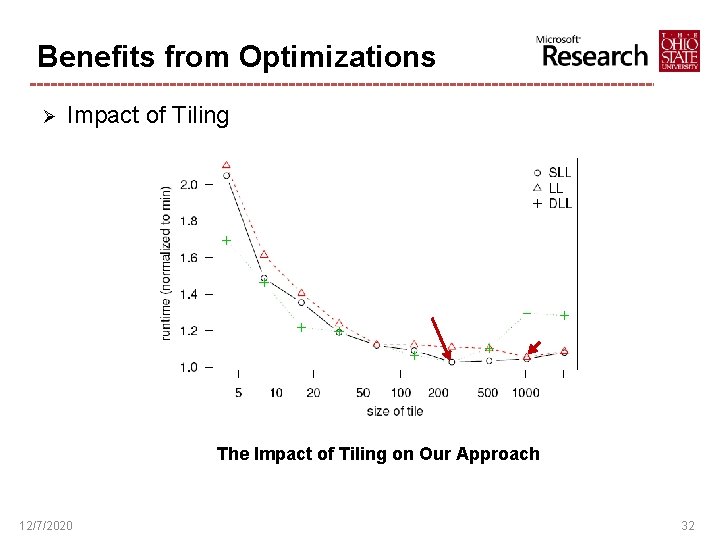
Parallelism Optimizations Ø Tiling trees into smaller bags ü ü ü Observation: Only a small number of trees are processed at the same time Total number of trees is N, and the number of trees in each bag is n, then within each bag, we linearize n trees by LL/SLL/DLL layout Tiling can improve the locality of deep levels of trees, especially for SLL and DLL layout 12/7/2020 31

Benefits from Optimizations Ø Impact of Tiling The Impact of Tiling on Our Approach 12/7/2020 32

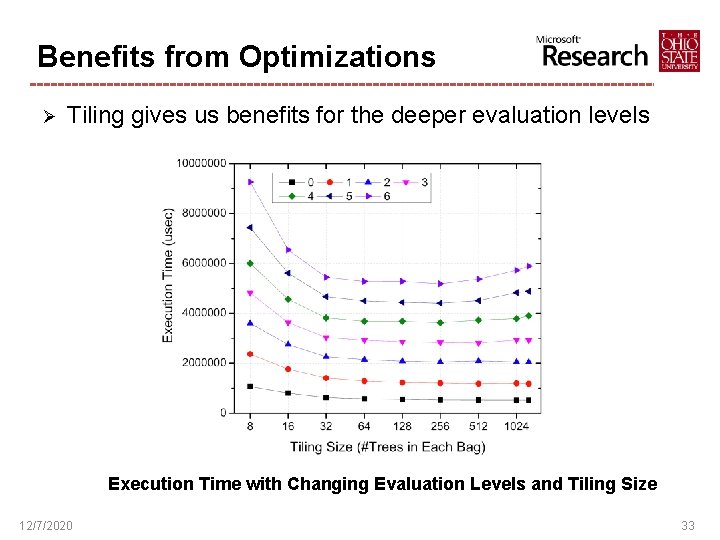
Benefits from Optimizations Ø Tiling gives us benefits for the deeper evaluation levels Execution Time with Changing Evaluation Levels and Tiling Size 12/7/2020 33