Silently review your notes and the returned assignments





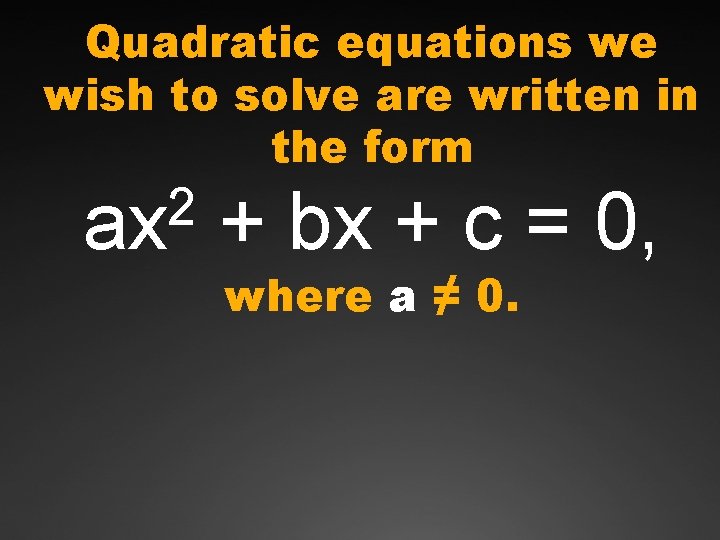


























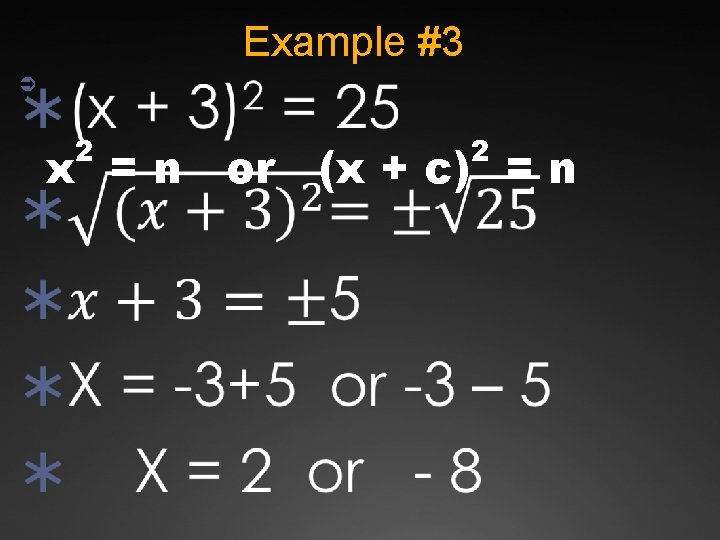
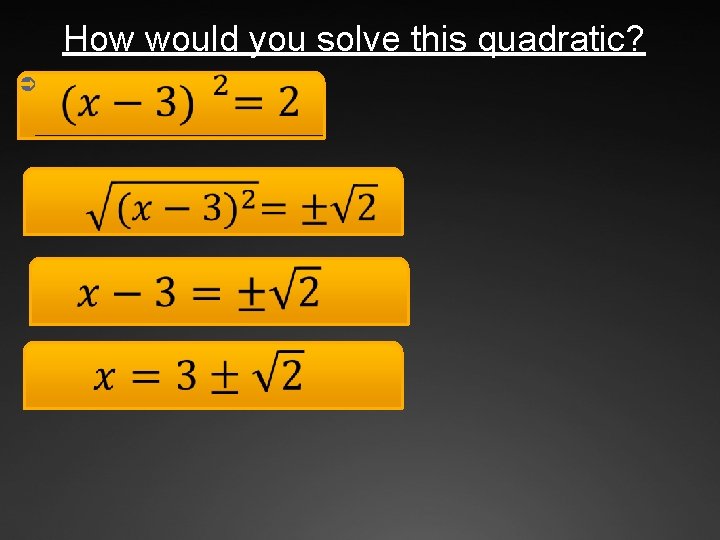




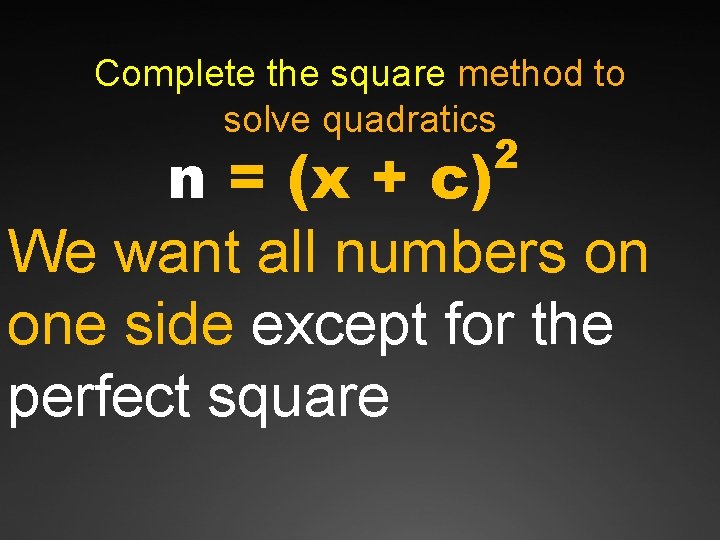
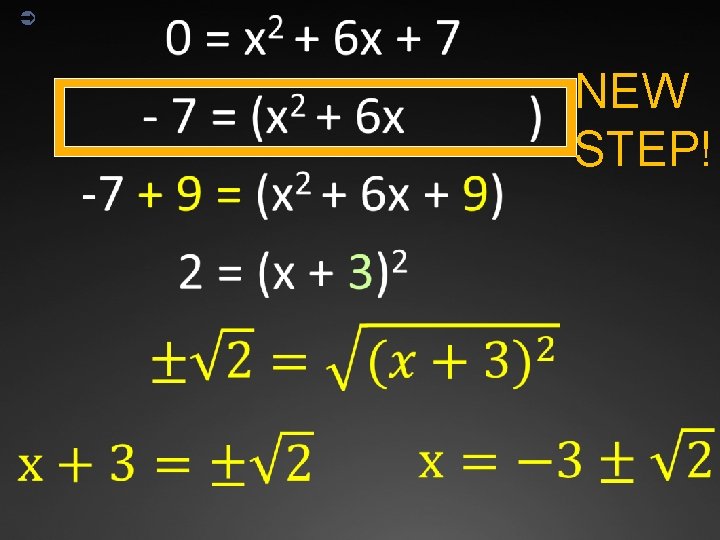










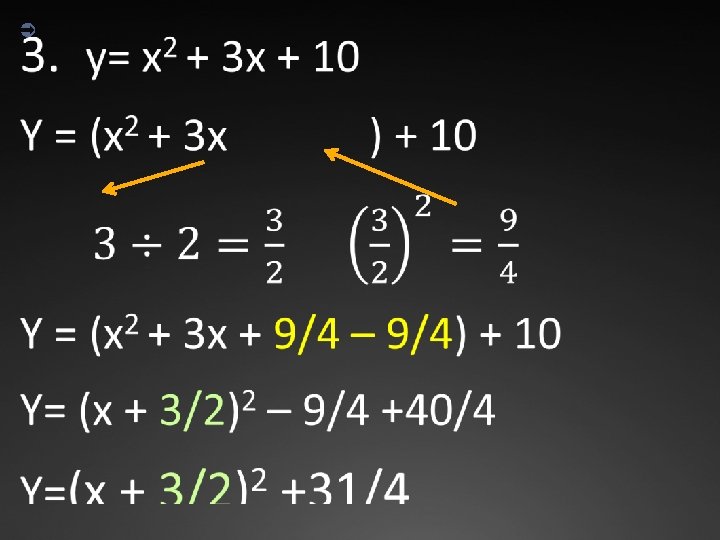

- Slides: 56

Silently review your notes and the returned assignments, Make sure you have turned all work in to be scored. ÜQuiz in 5 minutes on: ÜGraphing Quadratic Equations: Standard, Factored and Vertex form of the quadratic equation. Finding the root(s), x and y intercepts, completing the square.

Quiz ÜTurn in Factoring Worksheet from Friday

Zero product property

What does it mean to solve a quadratic?

Solving a quadratic means we: ÜFind the x intercepts ÜWhich are also known as roots or zeros.

Solving a quadratic means we are finding the ‘x’ values that when plugged into our quadratic make the equation = 0
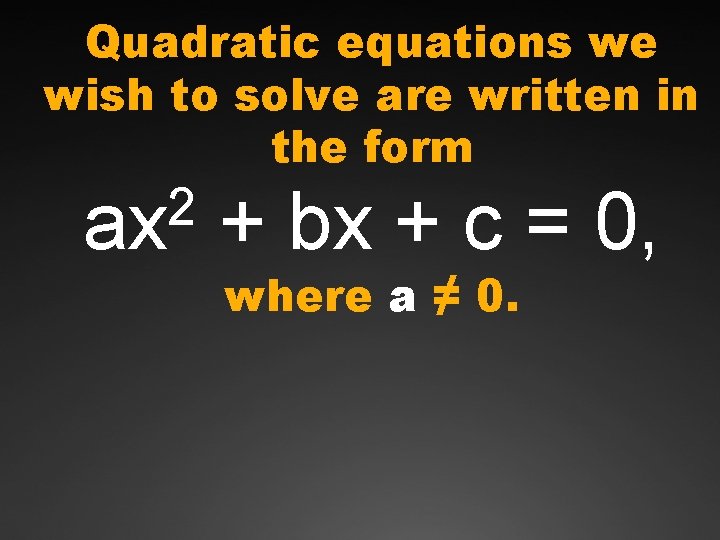
Quadratic equations we wish to solve are written in the form 2 ax + bx + c = 0, where a ≠ 0.

5 Methods Used to Solve Quadratic Equations 1. Graphing 2. Factoring 3. Square Root Property 4. Completing the Square 5. Quadratic Formula

Why so many methods? - Some methods will not work for all equations. - Some equations are much easier to solve using a particular method. - Variety is the spice of life.

Method 1: Graphing – reading the x-intercepts from the graph Üdoes not always produce an accurate result. ÜSome solutions are irrational or complex, ÜGraphing can be useful for word problems.

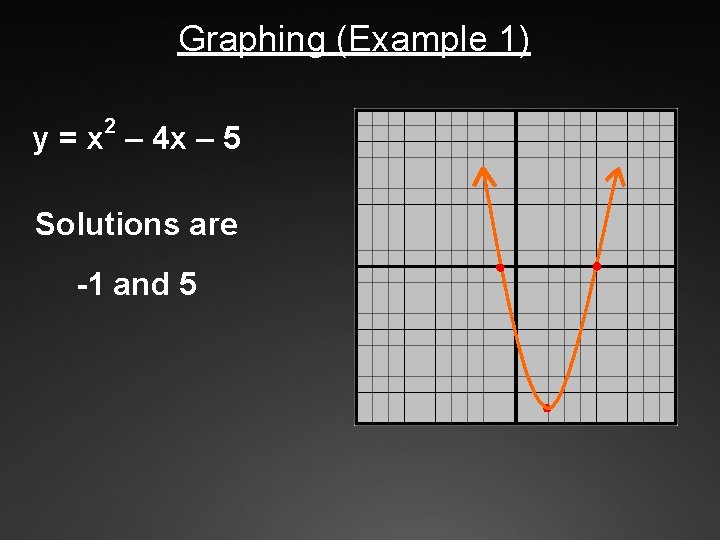
Graphing (Example 1) 2 y = x – 4 x – 5 Solutions are -1 and 5

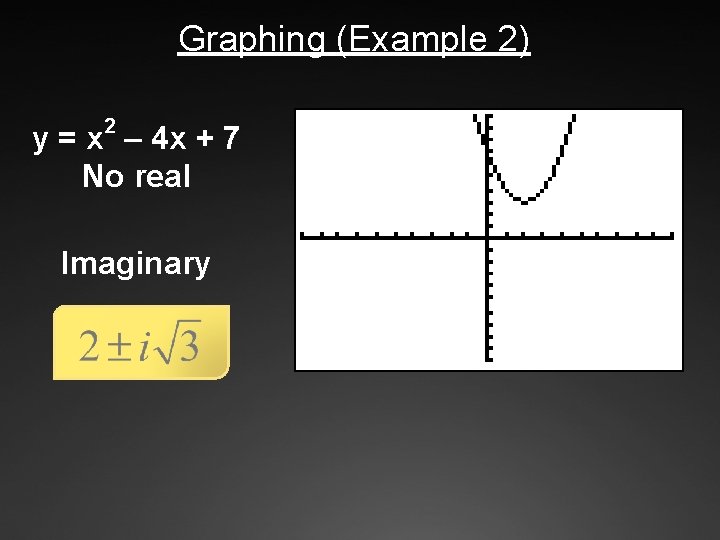
Graphing (Example 2) 2 y = x – 4 x + 7 No real Imaginary

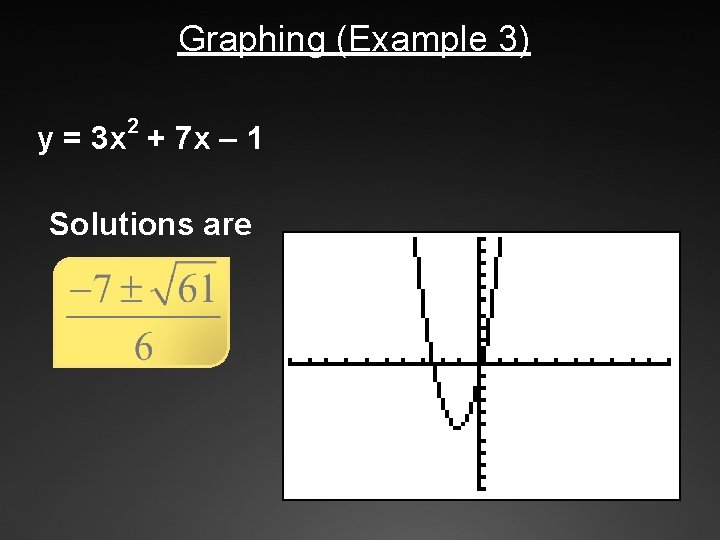
Graphing (Example 3) 2 y = 3 x + 7 x – 1 Solutions are

Method 2: Factoring (or Factorization) Üone of the easiest and quickest ways to solve quadratic equations; Ühowever, Ünot all quadratic polynomials can be factored. ÜThis means that factoring will not work to solve many quadratic equations.

Factoring ÜExample 1 Steps Ü 3 x +5 x = 0 1. Make one side of the ÜX(3 x + 5) = 0 2. Factor the other side 3. Use if ab=0 then a=0 and b=0 to solve. 2 Ü 3 x + 5 = 0 Üx = 0 Ü x = – 5/3 x = 0 equation 0, or setting y = 0 4. Solve for x

Factoring (Examples) Example 3 ÜExample 2 2 Üx – 24 = 0 Ü(x + 4)(x – 6) = 0 Üx + 4 = 0 x – 6 = 0 Ü x = – 4 x = 6 2 x – 8 x + 11 = 0 2 x – 8 x + 11 is Can’t factor

Basic factoring 2 y = x - 4 x + 4 y= (x - )(x - ) We are looking for what multiplies to 4 and adds to -4 How do we know we need two negative signs?

Basic factoring Y=x 2 - 4 x + 4 Y= (x - )(x - ) Y= (x - 2) I can check by foiling my answer.

Basic factoring 2 Y= x + 7 x +6 Y= (x + )(x + ) We are looking for what multiplies to 6 and adds to 7 How do we know we need two plus signs?

Basic factoring Y=x 2 + 7 x + 6 Y= (x + )(x + ) Y= (x + 1)(x + 6) I can check by foiling my answer.

Try factoring these problems Ü 1. 2 x 2 – 3 x Ü 2. 6 x 2 – 3 x X(2 x – 3) 3 X(2 x – 1) Ü 3. 2 x(x -1) + 3(x-1) (x -1)(2 x +3) Ü 4. 5 x(x + 3) – 4(x + 3) Ü 3. (3 x 2 –x) – (9 x – 3)

Try factoring these problems Ü 4. 5 x(x + 3) – 4(x + 3) (X + 3)(5 x – 4) 2 Ü 3. (3 x –x) – (9 x – 3) X(3 x – 1) – 3(3 x – 1)(x - 3)

Factoring more complex problems ÜWe need to be able to do these types of problems to be able to factor the really hard problems with leading coefficient greater than 1.

Factoring more complex problems WS

Factoring more complex problems ÜCoefficient in front of x 2 not equal to 1.

http: //www. youtube. com/watch? v=Jbbl. Z 9 a 7 t Hs Factoring when you have a leading coefficient other than 1

Example 1: Factor Set equation =0

1. Multiply the leading coefficient and the constant ac 2. Determine which factors of -12 can add to b, which is 1 3. Replace x with the new numbers determined in step 2.

3. Replace the middle term. 4. Group and factor out. Check to make sure ( ) are the same. 5. Move the common factor out front. Now you can solve and check answer.

Example 2: Factor Set equation =0

1. Multiply the leading coefficient and the constant ac 2. Determine which factors of -7 can add to b, which is 6 3. Replace the middle term with the new numbers determined in step 2.

3. Rewrite the quadratic and split the middle term. 4. Group and factor out. Check to make sure ( ) are the same. 5. Move the common factor out front. Now you can solve and check answer.

Square Roots What is a square root? 1. Gives us the side length of a square 5 25 36 6 2. Undoes squaring (inverse of taking a square)

Method 3: Square Roots Ü https: //www. desmos. com/calculator/5 exrajmhs 8

Method 3: Square Root Property ÜThis method is also relatively quick and easy; however, Üit only works for equations in which the quadratic polynomial is written in the following form. Ü 2 2 Ü x = n or (x + c) = n

Square Root Method(Examples) Ü Example 1 Example 2 2 x – 5 x + 11 = 0 X 2 = 49 x = +/- 7 2 This equation is not written in the correct form to use this method. 2 x = n or (x + c) = n
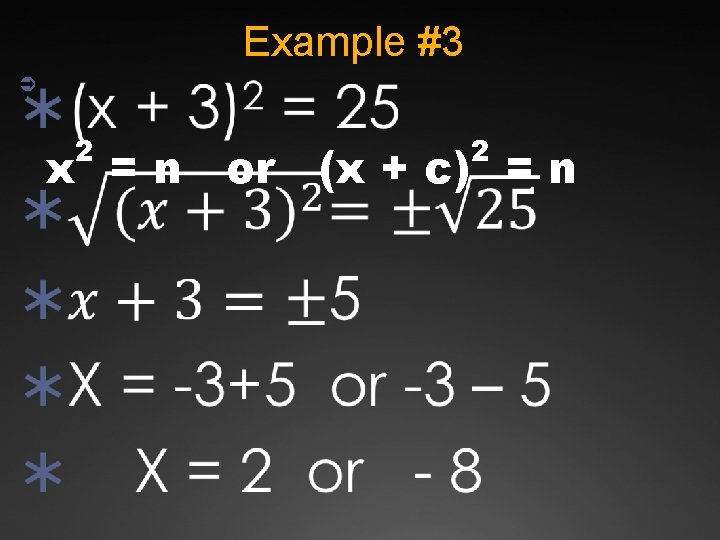
Example #3 Ü 2 2 x = n or (x + c) = n
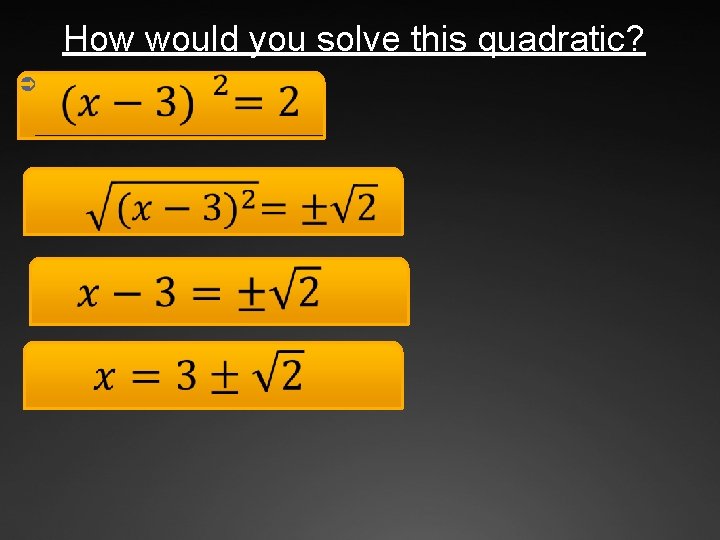
How would you solve this quadratic? Ü

Square root worksheet

Turn in Square root and worksheet on Factoring with a leading coefficient other than 1 packet take out notes

Completing the Square ÜThis method will work to solve ALL quadratic equations; Ühowever, Üit is “messy” to solve quadratic equations by completing the square if a ≠ 1 and/or b is an odd number. ÜCompleting the square is a great choice for solving quadratic equations if a = 1 and b is an even number.

Complete the square method to solve quadratics Ü
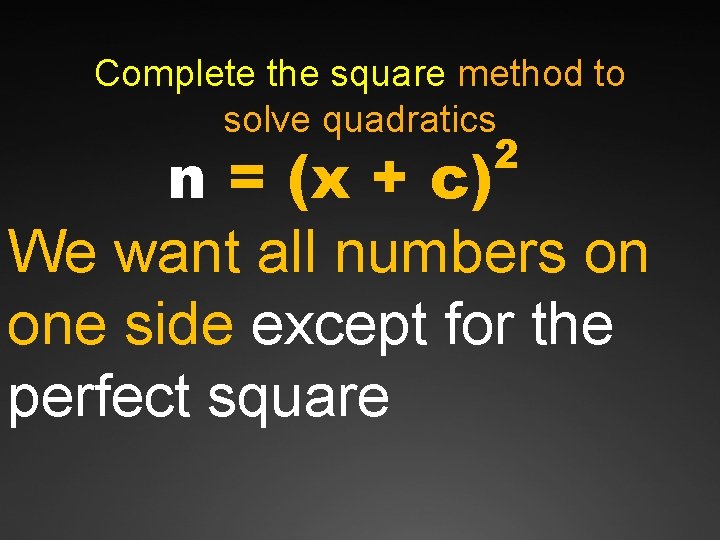
Complete the square method to solve quadratics 2 n = (x + c) We want all numbers on one side except for the perfect square
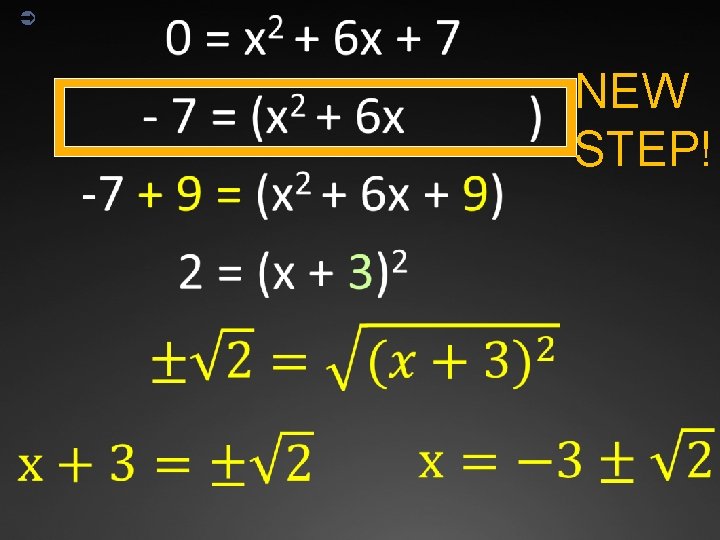
Ü NEW STEP!


Quadratic Formula ÜThis method will work to solve ALL quadratic equations; however, Üfor many equations it takes longer than some of the methods discussed earlier. ÜThe quadratic formula -good choice • if the quadratic cannot be factored, 2 • the equation cannot be written as (x+c) = n • a is not 1 and/or b is an odd number.

Quadratic Formula (Example) 2 x – 8 x – 17 = 0 a = 1 b = – 8 c = – 17

Find someone who was not here yesterday. Partner with them. Get out a sheet of paper and do exercise 8 C 2 a - e You have 15 minutes untill you turn it in.

Solving Quadratic word problems

Quadratic word problems Ü The length of a rectangle is 3 less than the width. The area is 54 sq. meters. What are the dimensions? Ü L x W is area Ü L = W - 3 Ü = (W - 3)(W) A= 54 m 2 Ü = W 2 – 3 W - 54 Ü (w – 9) (w + 6) =0 w = 9 w= - 6

Quadratic word problems Ü The length of a rectangle is 3 less than the width. The area is 54 sq. meters. Ü L x W is area Ü L = W - 3 Ü (w – 9) (w + 6) =0 9 meters A= 54 m 2 Ü w = 9 w= - 6 6 meters Ü Can’t have negative distance

Quadratic word problems The length of a rectangle is 3 times the Ü width. The area is 108 sq. meters. What are the dimensions? A=108 m 2

Quadratic word problems Ü A=108 m 2

Solve of x, more complex problems Ü 8 D. 1 #3 a - d, f Ü 1. Expand Ü 2. Move all terms to the left and Üset = 0 Ü 3. Factor (x - ) = 0 ÜHow to deal with x in denominator
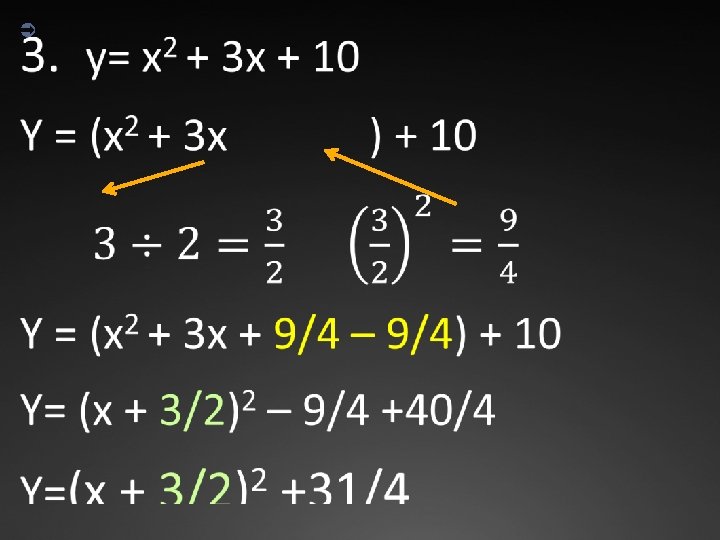

Completing the Square (Examples Ü Example 2 a ≠ 1, b is not even 3 x 2 – 5 x + 2 = 0 OR x = 1 OR x = ⅔