SILA SILA SILA SILA za poganjanje pedal pri

SILA SILA SILA SILA

• za poganjanje pedal pri kolesu je potrebna SILA • za dvig torbe iz tal na mizo je potrebna SILA • za to, da zviješ železno palico ali prestrižeš žico je potrebna SILA • sile lahko med seboj primerjamo po velikosti. • sile lahko merimo. sila je fizikalna količina

• Sile delujejo na telesa. • Pri preučevanju sil ločimo opazovano telo in okolico. • Na opazovano telo deluje s silo telo iz okolice. • Silo poimenujemo po telesu iz okolice, ki silo povzroča. – sila noge (na žogo) – sila vrvice (na sliko) – sila roke (na gobo) • Sile označujemo s črko F.

• Sile so vzrok za spremembe gibanja, lege ali oblike telesa. • Sila ima poleg velikosti tudi smer. • Količinam pri katerih določimo smer in velikost imenujemo vektorji. • Na vsa telesa na Zemlji deluje sila, ki jo imenujemo teža. Oznaka Fg. • Smer delovanja teže je navpično navzdol. • Velikost teže, ki deluje na telo je povezana z maso telesa. • Na telesi z enakima masama deluje enaka teža.

MERJENJE SIL

• Sila je fizikalna količina in jo lahko merimo. • Sile merimo v enotah , ki se imenujejo NEWTON-i (njutni). Oznaka je “N” • 1 N je enak sili, s katero Zemlja privlači utež z maso 100 g. 1 N je teža 100 g uteži. • Dve sili sta enaki, če na istem telesu povzročita enako spremembo. • Sile merimo s pomočjo prožni teles: vzmeti, elastika, kovinski trakovi, ….

• Naprava za merjenje sil se imenuje silomer ali vzmetna tehtnica. • Silomer je sestavljen iz prožnega telesa in merila. Prožno telo mora biti umerjeno. • Postopek umerjenja vzmeti. – Na vzmet dodajamo uteži z znano maso. – Zaradi teže uteži se vzmet razteza. Merimo raztezke in jih zapisujemo v tabelo. – S pomočjo podatkov v tabeli narišemo graf, ki prikazuje kako se raztezek spreminja s silo.

• Ugotovimo, da je raztezek sorazmeren s silo. Pravimo, da za vzmeti velja Hookov zakon. • Iz grafa določimo konstanto vzmeti “k”. • Ta nam pove za koliko se raztegne vzmet , če nanjo deluje sila 1 N. • Z umerjeno vzmetjo in šolskim ravnilom lahko merimo sile.

Risanje in seštevanje sil

Risanje sil • Sile smo se naučili meriti. • Vsakdanje izkušnje kažejo, da ima sila svojo smer. • Za količino, ki ima velikost in smer pravimo, da je vektorska količina ali vektor. Sila je tudi vektor. • Zato sile rišemo kot vektorje - usmerjene daljice.

• Dolžina daljice, ki jo narišemo je mera za velikost sile, smer daljice pa se ujema s smerjo sile. • Točka v kateri sila prijemlje pravimo prijemališče. Na sliki je to začetek daljice. • Na sliki bomo silo označili takole: • Sile rišemo v merilu. Na primer: M: 1 cm 2 N

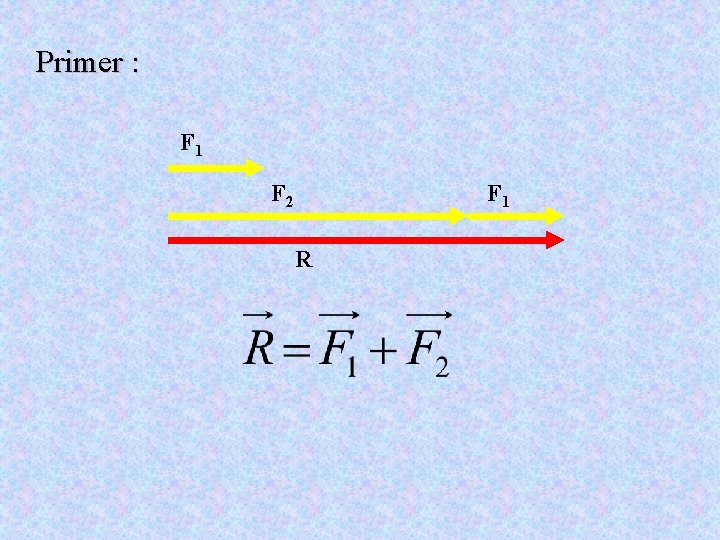
Seštevanje vzporednih sil • Če na telo deluje več sil hkrati jih lahko seštejemo. • Seštevamo jih kot vektorje. • Vsota sil je zopet sila, ki jo imenujemo rezultanta in jo označimo z • Pri seštevanju je pomembna velikost in smer sile, zato je najenostavnejše seštevati vzporedne sile.

Primer : F 1 F 2 F 1 R

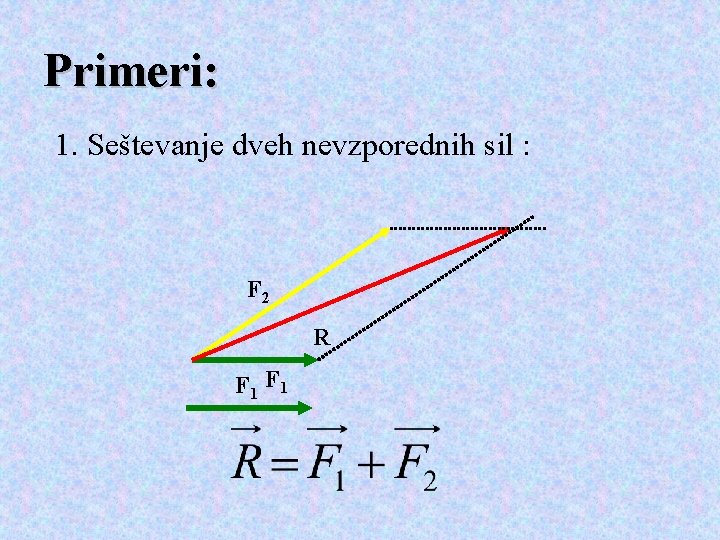
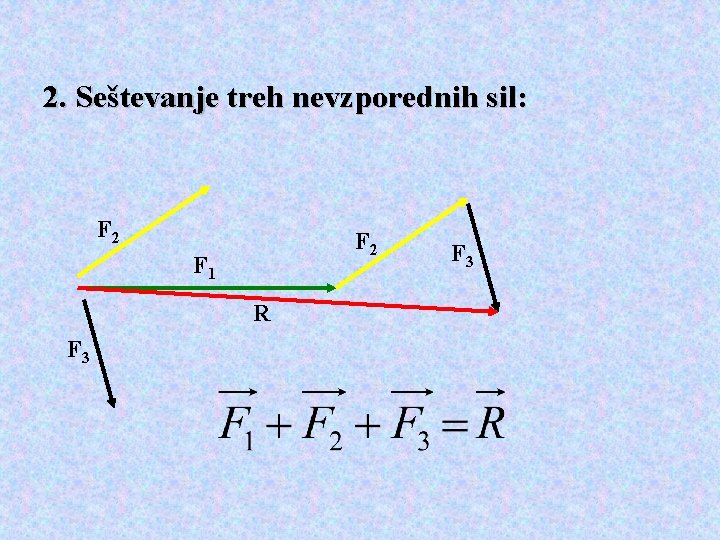
Seštevanje nevzporednih sil • Pri seštevanju nevzporednih sil rezultanta ni enaka aritmetični vsoti ali razliki velikosti posameznih sil. • Nujno moramo upoštevati smeri sil. Rezultanta je enaka vektorski vsoti sil. • Za seštevanje vektorjev sta znani trikotniško in paralelogramsko pravilo.

Primeri: 1. Seštevanje dveh nevzporednih sil : F 2 R F 1

2. Seštevanje treh nevzporednih sil: F 2 F 1 R F 3

Razstavljanje sil

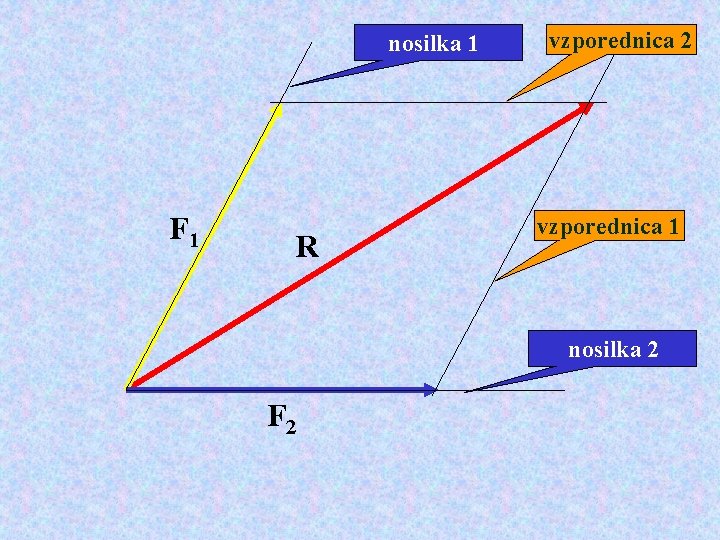
• Dve sili lahko po paralelogramskem pravilu seštejemo in dobimo rezultanto. • Sili iz katerih smo dobili rezultanto, imenujemo komponenti. • Nasprotni postopek od seštevanja sil se imenuje razstavljanje sil. • Z razstavljanjem rezultante dobimo dve komponenti.

• Razstavljanje rezultante poteka po naslednjem postopku : – k dani rezultanti narišemo črti nosilki, ki potekata v isto smer kot komponenti. – narišemo vzporednici črtam nosilkam skozi vrh rezultante – izvlečemo komponenti od izhodišča do presečišča nosilke in vzporednice.

nosilka 1 F 1 R vzporednica 2 vzporednica 1 nosilka 2 F 2