Significant Figures Accuracy and Precision Scientific Notation Scientific









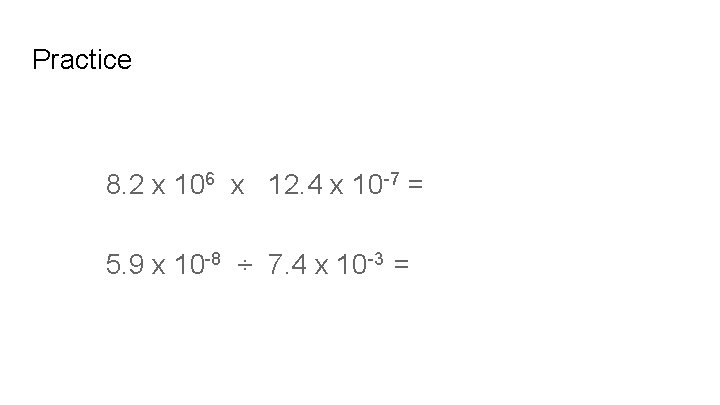



- Slides: 15

Significant Figures Accuracy and Precision Scientific Notation Scientific Method

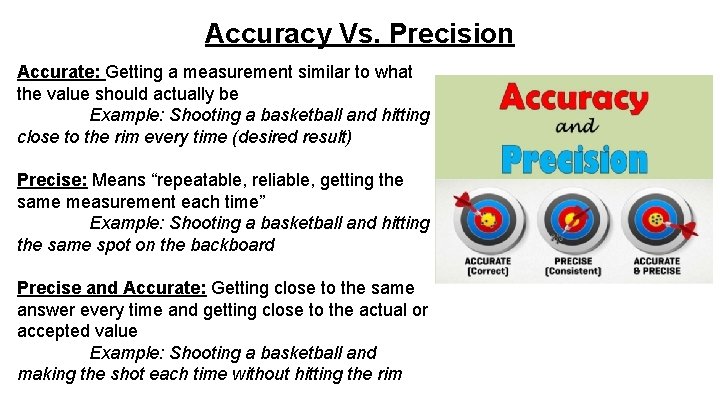
Accuracy Vs. Precision Accurate: Getting a measurement similar to what the value should actually be Example: Shooting a basketball and hitting close to the rim every time (desired result) Precise: Means “repeatable, reliable, getting the same measurement each time” Example: Shooting a basketball and hitting the same spot on the backboard Precise and Accurate: Getting close to the same answer every time and getting close to the actual or accepted value Example: Shooting a basketball and making the shot each time without hitting the rim

Measuring with Accuracy and Precision ● Measurements are limited to a certain number of digits by the precision of the measuring tool. ● In order to use an instrument accurately and precisely always estimate 1 decimal place pass the smallest increment.

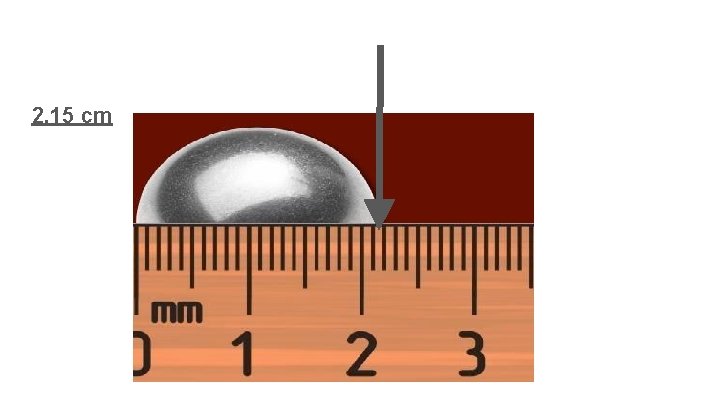
What would be the most accurate and precise measurement using the ruler?

2. 15 cm

What is correct measurement of this triple beam balance?

276. 23

Significant Figures ● The purpose of sig figs is to eliminate assumptions from your data. When measuring an object, we can only be as precise as our instrument enables us. ● For example, when using a ruler we can only read to the nearest mm or tenth of a cm, then estimate one more digit (tenth of a mm or hundreth of a cm).

Rules for Sig Figs ● Non-zero numbers count (1 -9) ● Zeros that are sandwiched between ● Any zero at the end of a decimal number (to the right) $14. 50 ● Zeros in front DO NOT count $0. 05 ● If you need to make a zero significant, place a line over or under that zero. ● In scientific notation, all digits are significant.

How Many Sig Figs? 421 has _____ sig figs 39, 059, 000 has _____ sig 3. 034 has _____ sig figs 3. 220 x 105 has _____ sig 82. 700 has _____ sig figs 800, 890 has _____ sig figs 0. 000365 has _____ sig figs 523, 000 has _____ sig figs

Multiplying/Dividing Sig Figs 3459← 4 sig figs x 25← 2 sig figs 86, 475← Answer without rounding 86, 000← Answer rounded to the proper number of sig figs According to Sig Fig rules the answer must have the same number of sig figs as the number with the least sig figs…in this case → 2 sig figs, so now you need to round the answer to 2 sig figs
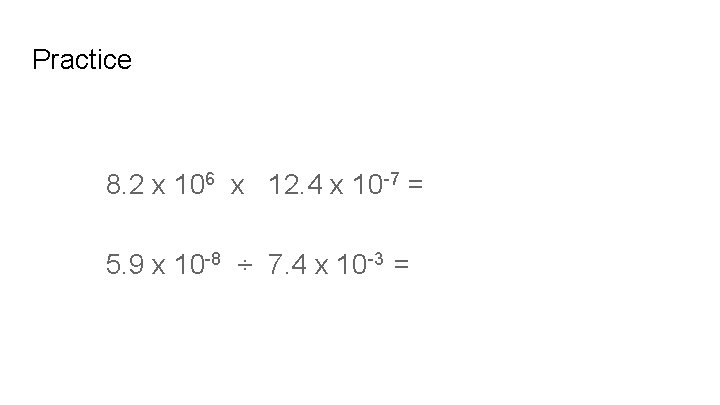
Practice 8. 2 x 106 x 12. 4 x 10 -7 = 5. 9 x 10 -8 ÷ 7. 4 x 10 -3 =

8. 2 x 106 x 12. 4 x 10 -7 = 1. 0 x 101 5. 9 x 10 -8 ÷ 7. 4 x 10 -3 = 8. 0 x 10 -6 – Multiply and/or divide as indicated in the problem. – Then round the answer to the same number of sig figs as the smallest number of sig figs of the numbers being multiplied or divided.

Scientific Method Scientific method – a method scientist use to gain, organize and apply new knowledge. I – State the Problem II – Make a Hypothesis ( about the answer to the problem ) III – Make a Prediction ( about the hypothesis ) IV – Perform an Experiment ( to test the prediction and collect data 0 V – Analyze the results of the Data IV – Draw a Conclusion ( that relates to your analysis )

hypothesis - an educated guess observations – the act of recording something that you ( see, hear, touch, smell, taste ) precision – to measure with scientific exactness ( accuracy ) accuracy – as near to the true value ( precision ) variable – something that will change in an experiment inference – to draw a reasonable / logical conclusion from evidence that is known to be true ( deductive reasoning ) conclusion – the result or outcome of a process ( lab experiment ) standard notation- the manner in which numbers are normally written for math scientific notation – a way to express values too large and small to be conveniently written in standard notation dimensional analysis – a method of converting units by using a conversion factor that equals 1 conversion factor - A numerical factor used to multiply or divide a quantity when converting from one system of units to another. quantitative – a measurement in numerical form ( an amount of something ) qualitative – of or pertaining to the value of something