SIGNALTEORI Hva skal vi med det da Sinussignalet

SIGNALTEORI, Hva skal vi med det da? • Sinussignalet, byggesteinen i signalteorien – Hvordan måler vi størrelsen på sinussignalet – Hvordan oppfatter vi frekvens og nivå • Frekvensanalyse – FFT, tidsvindu og frekvensvindu – Frekvensavbildning av periodiske og ikkeperiodiske signal – Pulsrespons • Filterteori (systemers frekvenssvar) – Lavpass, høypass, båndpass og resonnansfilter

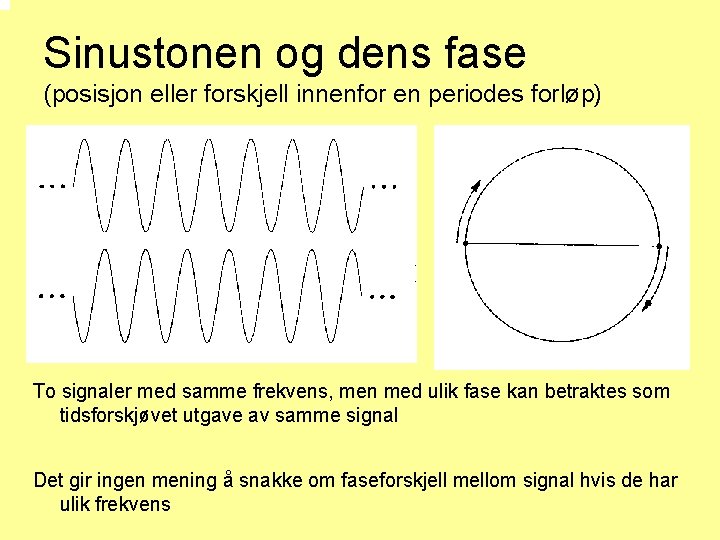
Sinustonen og dens fase (posisjon eller forskjell innenfor en periodes forløp) To signaler med samme frekvens, men med ulik fase kan betraktes som tidsforskjøvet utgave av samme signal Det gir ingen mening å snakke om faseforskjell mellom signal hvis de har ulik frekvens

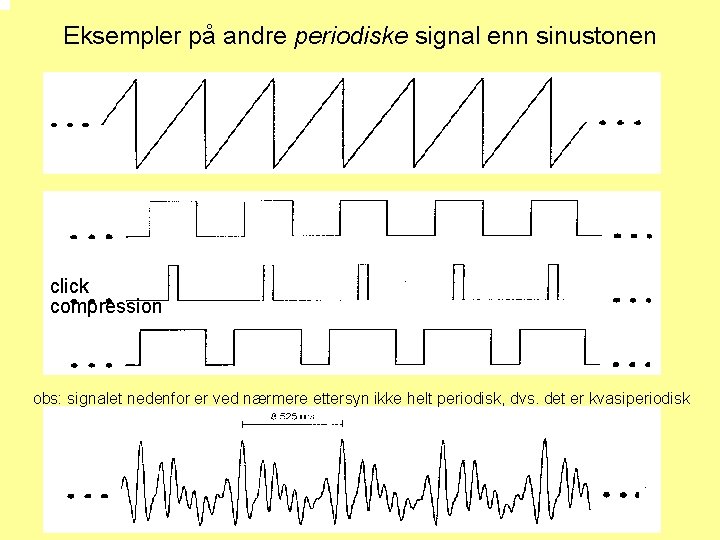
Eksempler på andre periodiske signal enn sinustonen click compression obs: signalet nedenfor er ved nærmere ettersyn ikke helt periodisk, dvs. det er kvasiperiodisk

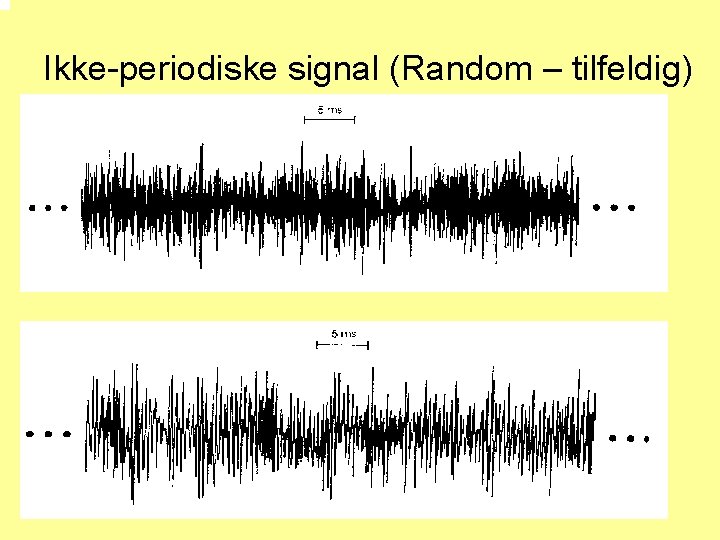
Ikke-periodiske signal (Random – tilfeldig)

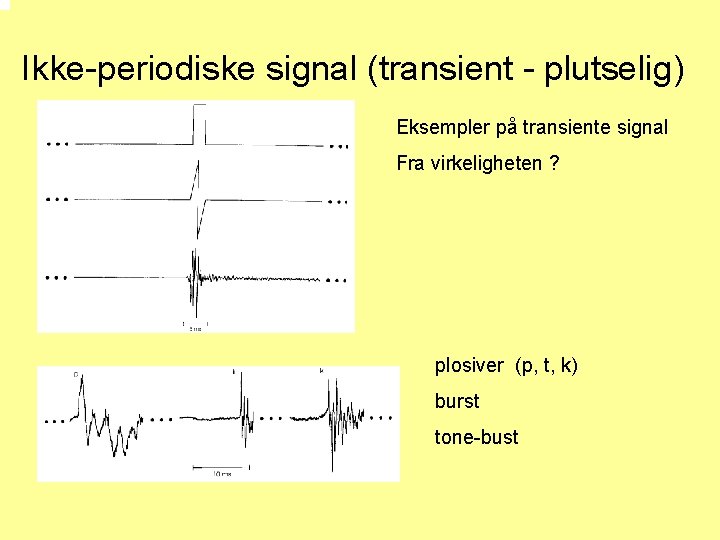
Ikke-periodiske signal (transient - plutselig) Eksempler på transiente signal Fra virkeligheten ? plosiver (p, t, k) burst tone-bust

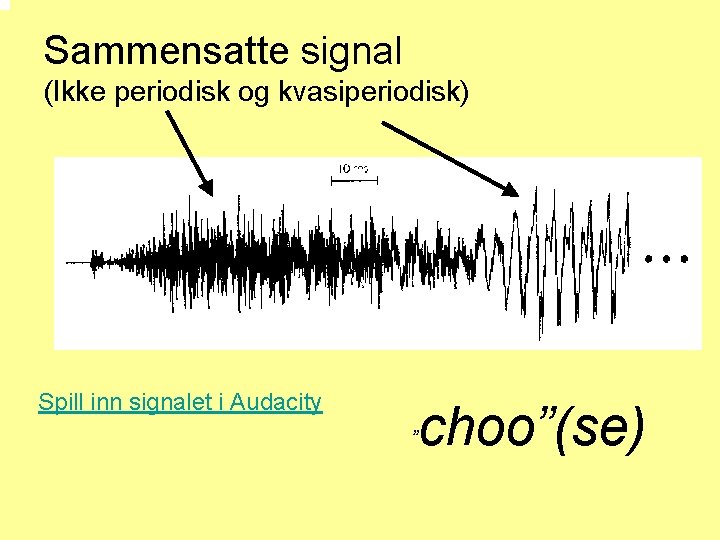
Sammensatte signal (Ikke periodisk og kvasiperiodisk) Spill inn signalet i Audacity ” choo”(se)

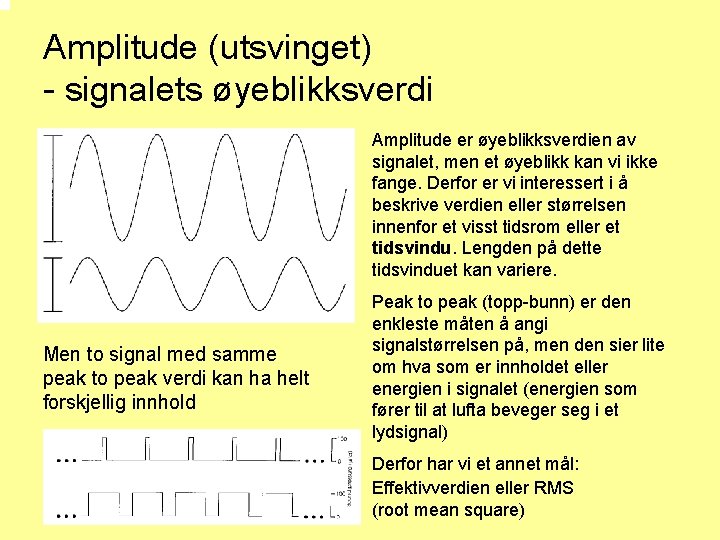
Amplitude (utsvinget) - signalets øyeblikksverdi Amplitude er øyeblikksverdien av signalet, men et øyeblikk kan vi ikke fange. Derfor er vi interessert i å beskrive verdien eller størrelsen innenfor et visst tidsrom eller et tidsvindu. Lengden på dette tidsvinduet kan variere. Men to signal med samme peak to peak verdi kan ha helt forskjellig innhold Peak to peak (topp-bunn) er den enkleste måten å angi signalstørrelsen på, men den sier lite om hva som er innholdet eller energien i signalet (energien som fører til at lufta beveger seg i et lydsignal) Derfor har vi et annet mål: Effektivverdien eller RMS (root mean square)

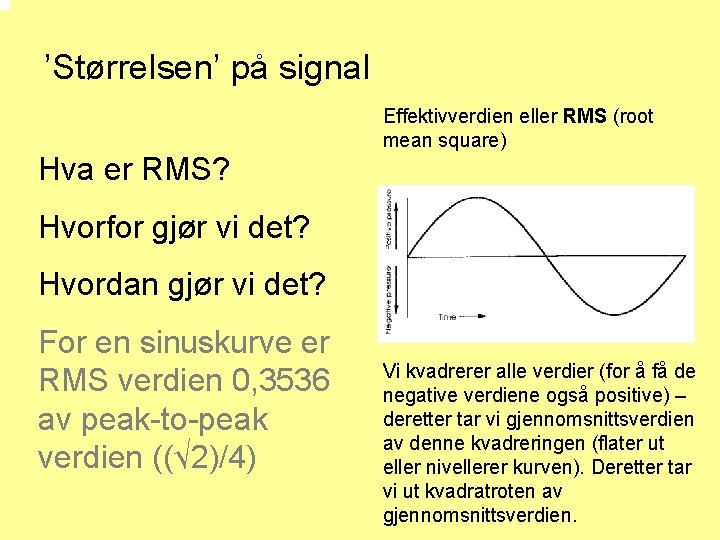
’Størrelsen’ på signal Hva er RMS? Effektivverdien eller RMS (root mean square) Hvorfor gjør vi det? Hvordan gjør vi det? For en sinuskurve er RMS verdien 0, 3536 av peak-to-peak verdien ((√ 2)/4) Vi kvadrerer alle verdier (for å få de negative verdiene også positive) – deretter tar vi gjennomsnittsverdien av denne kvadreringen (flater ut eller nivellerer kurven). Deretter tar vi ut kvadratroten av gjennomsnittsverdien.

RMS variasjonen avhenger av tidsvinduet Root Mean Square → Mean = gjennomsnitt - av hva? - av amplitudevariasjonene i et tidsvindu Hvis det tidsvinduet vi tar gjennomsnitt av er langt vil variasjonene være langsomme Hvis det tidsvinduet vi tar gjennomsnitt av er kort vil variasjonene være hurtige Tidskonstanter for RMS målinger: Impulse 35 msek Fast 125 msek Slow 2 sek Hvordan foregår en slik gjennomsnittstsmåling HER ER TRE EKSEMPEL

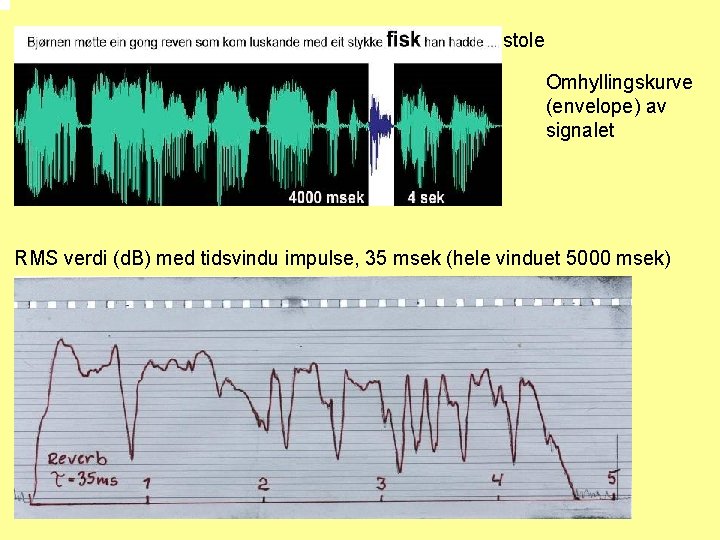
stole Omhyllingskurve (envelope) av signalet RMS verdi (d. B) med tidsvindu impulse, 35 msek (hele vinduet 5000 msek)

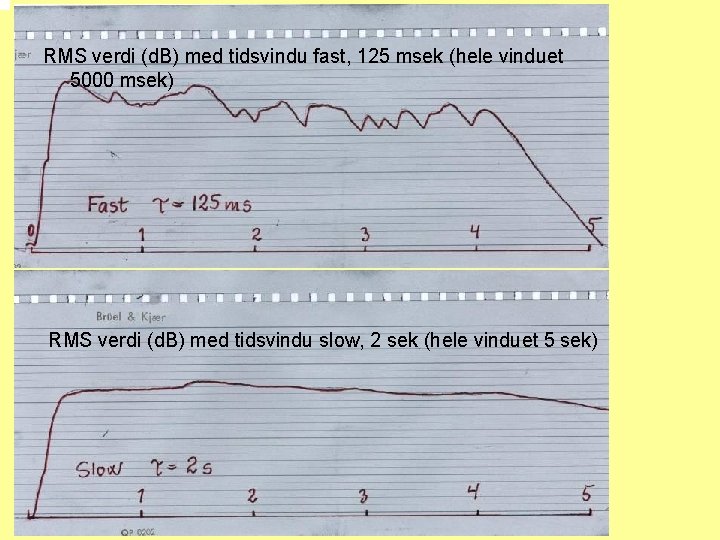
RMS verdi (d. B) med tidsvindu fast, 125 msek (hele vinduet 5000 msek) RMS verdi (d. B) med tidsvindu slow, 2 sek (hele vinduet 5 sek)

VARIASJONER AV FREKVENS OG STYRKE er så store (fra den minste til den største) at vi må ta i bruk spesielle skalaer. VI SER PÅ LYDEN FISK: Dette er utsnitt av is i fisk

LA OSS FØRST SE LITT PÅ FREKVENS Variasjonsområdet for frekvens er veldig stort - fra 20 til 20 000 forholdstallet er som 1: 1000 (3 dekader)* - dette er likevel tall som det går an å forholde seg til VI HAR ET STØRRE PROMLEM FOR STYRKE: Variasjonsområdet for styrke (RMS) er mye større -Størrelsesorden 0, 00002 N/m 2 (terskel) til 200 N/m 2 (smerte) eller 20 – 200 000 µPa (micro Pascal) forholdstallet er som 1: 10 000 (7 dekader)* *) dekade (fra prefikset deka som betyr ti eller ti ganger)

VI FÅR HJELP AV SANSENE VÅRE ! Alle sansene, inklusive hørselen, er ’konstruert’ for å oppfatte endringer i forhold til ’ett eller annet’ eller ”multiplikasjons og divisjonskonstruert” Hørselen oppfatter en økning, for eksempel til det doble (det tredoble eller det firedoble osv. ) som likt – uansett hvor vi er på skalaen Dette har konsekvenser både for oppfattelse av lydstyrke og tonehøyde. Konsekvensene er at vi må omdefinere skalaene Vi bruker ikke addisjons og subtraksjonsskalaer som på linjalen. Nei, vi bruker multiplikasjons og divisjonsskalaer der en viss lengde på skalaen betyr en multiplikasjon eller en divisjon med et visst tall

Skalaen for frekvens blir da ikke slik: 20 21 22 23 24 25 26 ……………… 14996 14997 14998 14999 15000 men slik: 20 40 80 160 320 640 1280 2560 5120 10240 (20480) Og vi må omdefinere skalaen for lydstyrke fra 0, 00002 0, 00003 0, 00004 0, 00005 ………… 19, 99997 19, 99998 19, 99999 20, 00 til (10 - ganging for hvert trinn) 0, 00002 0, 00020 0, 00200 0, 02000 0, 20000 2, 00000 200, 00000 Dette er multiplikasjonsskalaer eller det vi kaller vi logaritmiske skalaer, fordi vi hele tiden ganger med ett visst tall i stedet for å legge til, når vi beveger oss oppover på skalaen (eller vi dividerer med et visst tall når vi beveger oss nedover).

For antall svingninger pr. sekund bruker vi betegnelsen Hertz, forkortet Hz. Fordi forskjellen på tallverdien ikke er så svimlende stor (ca 20 til 15000) bruker vi tallverdiene slik de er, men vi framstiller dem alltid langs en logaritmisk skala. En fordobling eller en halvering av antall Hz, kaller vi en oktavavstand eller et oktavintervall. En multiplisering med 1, 26 er et såkalt 1/3 oktav intervall (1, 26 * 1, 26 = 2). I audiologien er vi altså ”splittet” i vår bruk av lineær og psykofysisk skala. Frekvensskalaen er logaritmisk, mens tallene er lineært angitt. Musikerne er mer rendyrkede psykofysikere, de snakker om intervaller 100 200 500 600 1000 1100 2000 2100 4000 4100

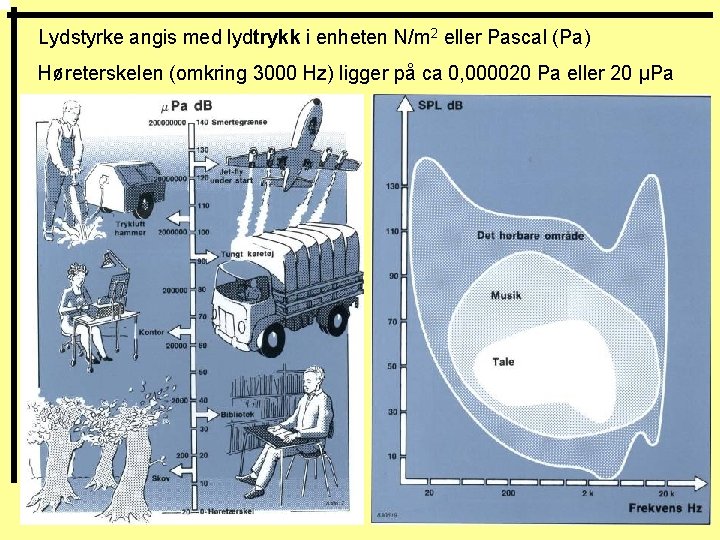
Lydstyrke angis med lydtrykk i enheten N/m 2 eller Pascal (Pa) Høreterskelen (omkring 3000 Hz) ligger på ca 0, 000020 Pa eller 20 µPa

Vi har en skala som går fra 20 til 200 000 (micro Pascal) eller med andre tall et forhold på 1 til 10 000. Her er det mer hensiktsmessig å bruke en multiplikasjonsskala eller det vi kaller en logaritmisk angivelse. For eksempel at vi starter ved høreterskel på 0, 00002 N/m 2 og kaller dette for et nullpunkt (logaritmisk), selv om dette slettes ikke er fravær av lydtrykk! For hver gang vi ganger lydtrykket med 3, 16 (10 0, 5) får vi en økning som tilsvarer omtrent en subjektiv fordobling. Dette kaller vi så en økning på 1 Bel, eller mer gjenkjennelig: 10 desibel, forkortet 10 d. B. Vi deler så inn skalaen logaritmisk fra 0 til 140 d. B. Vi kan framstille dette trinn for trinn

Skala for lydstyrke (d. B) 1(2) • Vi snakker om lydstyrke, men den subjektive oppfattelse forholder seg til lydens intensitet. • For å definere en intensitetsskala trenger vi et nullpunkt og en metode for å bestemme trinnenes størrelse • Alexander Graham Bell definerte bel som (10 er-)logaritmen til forholdet mellom en viss lydintensitet og en referanseintensitet (nær høreterskelen i binauralt fritt felt ved ca 2000 Hz) • En økning av intensiteten på 1 Bel tilsvarer en subjektiv lydstyrkefordobling • bel (B) = log (I / Iref) - en desibel er en tiendedels bel og antallet desibel blir da 10 ganger så stort i forhold til bel. • Altså desibel (d. B) = 10 log (I/Iref) • Intensiteten er proporsjonal (k) med kvadratet av lydtrykket: I = kp 2 • Tilsvarende blir da referanselydtrykket Iref = kpref 2 • Desibelverdien av lydstyrken blir da 10 log (I/Iref) = 10 log(kp 2/ kpref 2 ) - som vi kan omforme på følgende måte:

Skala for lydstyrke (d. B) 2(2) …. . forts • 10 log(kp 2/ kpref 2) (vi stryker k over og under brøkstreken): • = 10 log(p 2/ pref 2) (vi trekker kvadratet ut av parentesen siden både p og pref er kvadrert ): • = 10 log(p / pref)2 ( og siden log til et tall opphøyet i 2. er 2 ganger log til tallet, får vi): • = 2 * 10 log(p / pref) • = 20 log (p / pref) • pref er 20 µPa (micropascal) eller 0, 00002 Pa = 0 d. B SPL • Hvis pref er et fritt valgt utgangspunkt på d. B skalaen og vi skal regne om et d. B forhold til en multiplikasjonsfaktor kan vi stille opp følgende sammenheng: d. B-endringen = 20 log(multiplikasjonsfaktoren) eller d. B-endringen /20 = log (multiplikasjonsfaktoren) eller 10^(d. B-endringen/20) = multiplikasjonsfaktoren Vi skal øve litt videre på regning mellom d. B skala og trykkskala eller d. B skala og nivåskala – med regneark

Regning med d. B • • Faktor 1, 26 Faktor 1, 41 Faktor 2 Faktor 3, 16 Faktor 4 Faktor 5 Faktor 10 tilsvarer 0 d. B tilsvarer 2 d. B tilsvarer 3 d. B tilsvarer 6 d. B tilsvarer 10 d. B tilsvarer 12 d. B tilsvarer 14 d. B tilsvarer 20 d. B HUSK: Multiplikasjon - legge til d. B Divisjon - trekke fra d. B 9 d. B (3+3+3) = Faktor 1, 41 * Faktor 1, 41 16 d. B (10+6)= Faktor 3, 16 * Faktor 2 (se eget utlagt regne 8 d. B (10 -2)= Faktor 3, 16 / Faktor 1, 26 ark for omregning og gjør øvingsoppgavene i boka, side 40)

FFT tidsvindu og frekvensvindu • Et sinussignal gir et spektrum med en linje • Et hvilket som helst periodisk signal er sammensatt av en grunnfrekvens + multipler av grunnfrekvensen med bestemt amplitude og fase - Et periodisk signal har således et ideelt linjespektrum • Et ikkeperiodisk signal har ingen bestemt sammensetning og derfor et kontinuerlig spektrum • Et pulssignal av uendelig kort varighet har et flatt spektrum (som hvit støy) • Se på syntese av periodiske signal i regneark • Se på analyse av signal i audacity

Filterteori – Systemers frekvenssvar R & H kap. 6 amplitudesvar og fasesvar (respons) … hvordan et system ’behandler’ de ulike frekvenser (sinustoner) som går gjennom systemet - Hvordan amplituden og fasen endres. AMPLITUDE som forholdstall (x) og desibeltall og FASE som tidsforsinkelse og vinkeldreining Filter: høypass, lavpass, båndstopp, resonans, antiresonans § Karakteristika: knekkfrekvens, grensefrekvens, båndbredde, flankesteilhet, Q-faktor § Systemer i kaskade (serie) og i parallell Steilhet Knekk frekvens Bånd bredde Øvre grense frekvens Nedre grense frekvens Senter frekvens Q-faktor Høypass X X Lavpass X X X X Resonans X X Antiresonans X X Båndpass Båndstopp

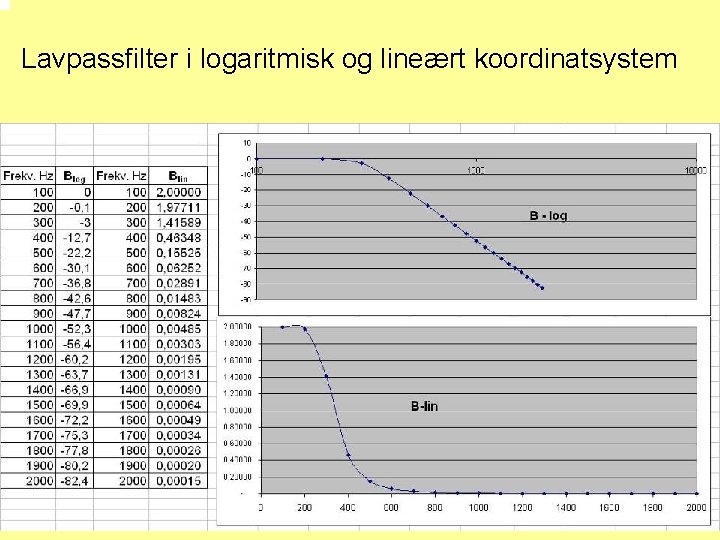
Lavpassfilter i logaritmisk og lineært koordinatsystem

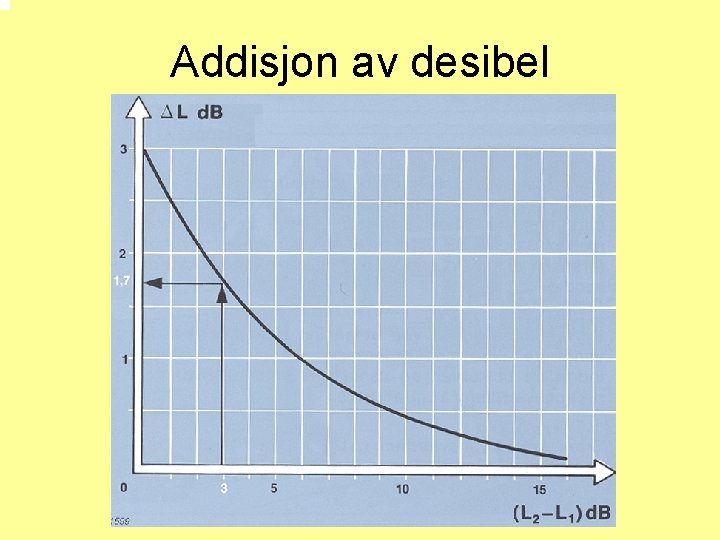
Hvor mye energi går gjennom et filter? • Jo bredere filter jo mer energi • En filterbank har en samlet energigjennomgang som er lik summen av energien gjennom alle filterene • En 1/3 oktav bank adderer opp totalnivået som summen av alle spektralnivåene • Energisummasjon: Like nivå øker totalniået med 3 d. B • Ørets hørselbåndsfilter (24) har ingen fast definisjon og vi bruker derfor ofte begrepet ERB (Ekvivalent Rektangulært Bånd) • Addisjon av desibelnivå foregår slik:

Addisjon av desibel

Power. Point diverse Dillon + Rosen & Howell