SignalSpace Analysis Introduction Geometric Representation of Signals Conversion

Signal-Space Analysis • Introduction • Geometric Representation of Signals • Conversion of the Continuous AWGN Channel into a Vector Channel • Likelihood Functions • Coherent Detection of Signals in Noise: Maximum Likelihood Decoding • Correlation Receiver • Probability of Error 2

Introduction (1) Message source emits one symbol from a M symbol alphabet which are equally likely. Probability of emission symbol mi : Transmitter codes mi to si(t) (real-valued energy signal) Two assumptions: • Channel is linear with wide enough bandwidth. no distortion • Channel noise is zero-mean white Gaussian. 3

Introduction (2) Additive White Gaussian Noise (AWGN) channel : Average probability of symbol error: Design goal: Optimum receiver with minimum probability of error. 4

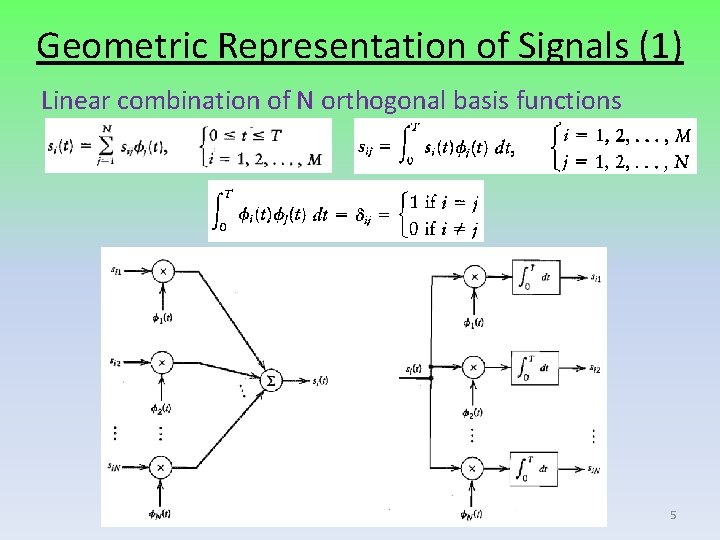
Geometric Representation of Signals (1) Linear combination of N orthogonal basis functions 5

Geometric Representation of Signals (2) Set of coefficients {sij} N-dimensional vector si • Vector si bears a one-to-one relationship with si(t) • Vector si is called signal vector. • set of signal vectors {si I i=1, 2, …, M} M point in an N-dimensional Euclidean space Example: N=2 , M=3 3 signals in 2 dimensional space 6

Geometric Representation of Signals (3) Pair of signals si(t) and sk(t) are represented by vectors si and sk. Euclidean distance between vector points: 7

Geometric Representation of Signals (4) Gram-Schmidt Orthogonalization Procedure 8

Geometric Representation of Signals (5) Gram-Schmidt Orthogonalization Procedure (generalization) Notice: N ≤ M 9

Conversion of the AWGN Channel (1) Received Signal: Correlator Output: 10

Conversion of the AWGN Channel (2) Statistical Characterization of the Correlation Outputs 11

Conversion of the AWGN Channel (3) Statistical Characterization of the Correlation Outputs 12

Conversion of the AWGN Channel (4) Conditional Probability Density Function: Theorem of Irrelevance: Insofar as signal detection in additive white Gaussian noise is concerned, only the projections of the noise onto the basis functions of the signal set affects the sufficient statistics of the detection problem; the remainder of the noise is irrelevant. 13

Likelihood Functions Conditional Probability Density Function: Likelihood Function: Log Likelihood Function: Ignoring 14

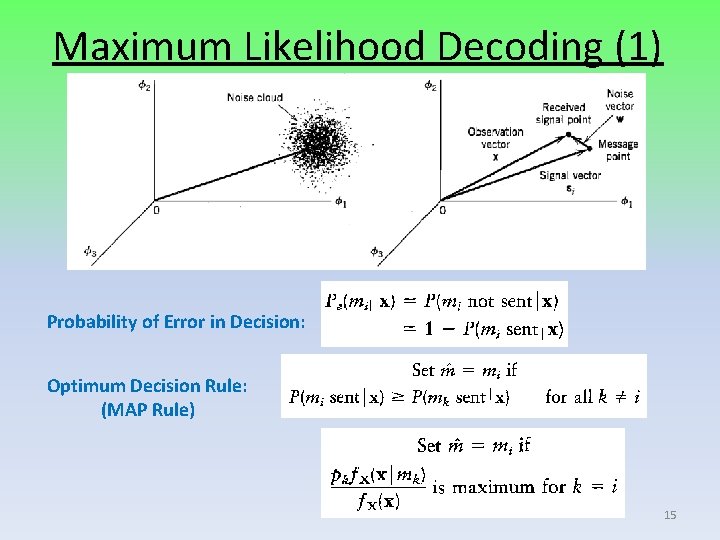
Maximum Likelihood Decoding (1) Probability of Error in Decision: Optimum Decision Rule: (MAP Rule) 15

Maximum Likelihood Decoding (2) Optimum Decision Rule: (MAP Rule) Total observation region is partitioned into M-decision regions, Z 1, Z 2, …, ZM 16

Maximum Likelihood Decoding (3) Maximum Likelihood Decision Rule: 17

Maximum Likelihood Decoding (4) 18

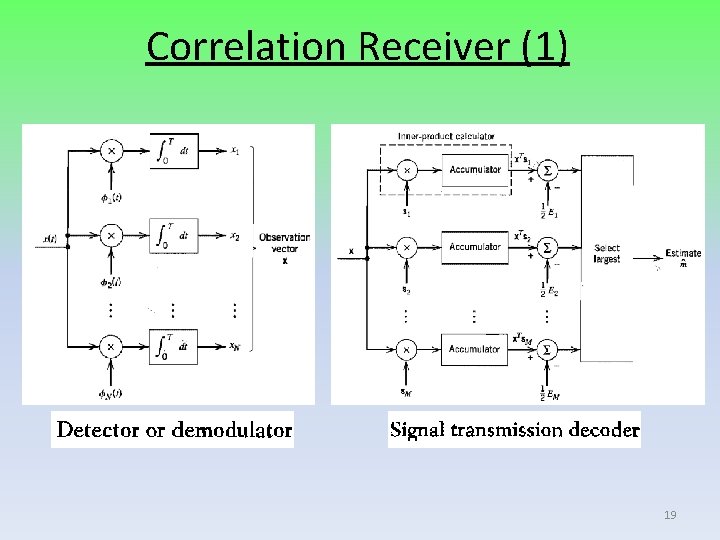
Correlation Receiver (1) 19

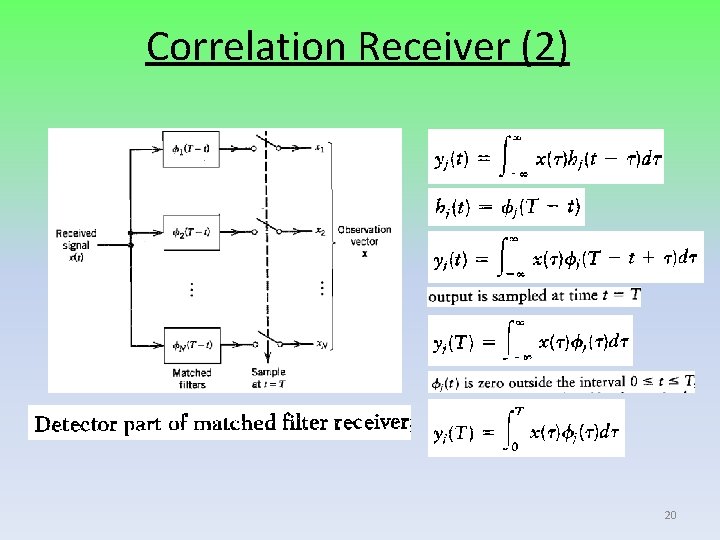
Correlation Receiver (2) 20

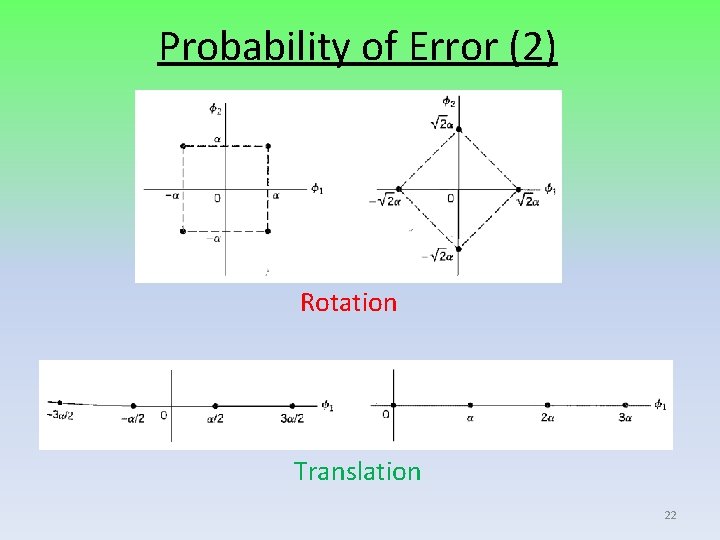
Probability of Error (1) Average probability of symbol error Probability of error is invariant to rotation and translation, Because: 1) In maximum likelihood detection, the probability of symbol error Pe depends solely on the relative Euclidean distances between the message points in the constellation. 2) The additive white Gaussian noise is spherically symmetric in all directions in the signal space. 21

Probability of Error (2) Rotation Translation 22

Probability of Error (3) (Minimum Energy Signals) Average energy of the translated constellation Average energy of the original constellation Differentiating with respect to a 23

Probability of Error (4) (Union Bound on the Probability of Error) Probability of Error: Pairwise Error Probability: 24

Probability of Error (5) (Union Bound on the Probability of Error) Averaging over all M symbols Circularly Symmetric Constellation 25

Probability of Error (6) (Bit versus Symbol Error Probabilities) Case 1: M-ary Modulation, Low probability of error, Gray code Most probable number of bit errors is one. Case 2: Mary Modulation, Symbol errors are equally likely Large M 26