SIGNALS SYSTEMS ENT 281 Chapter 1 Signals Systems

























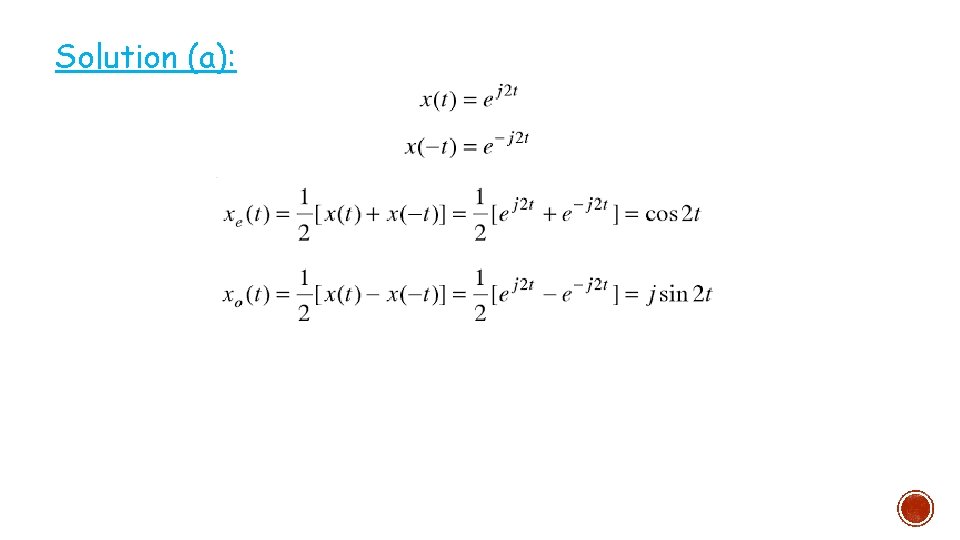
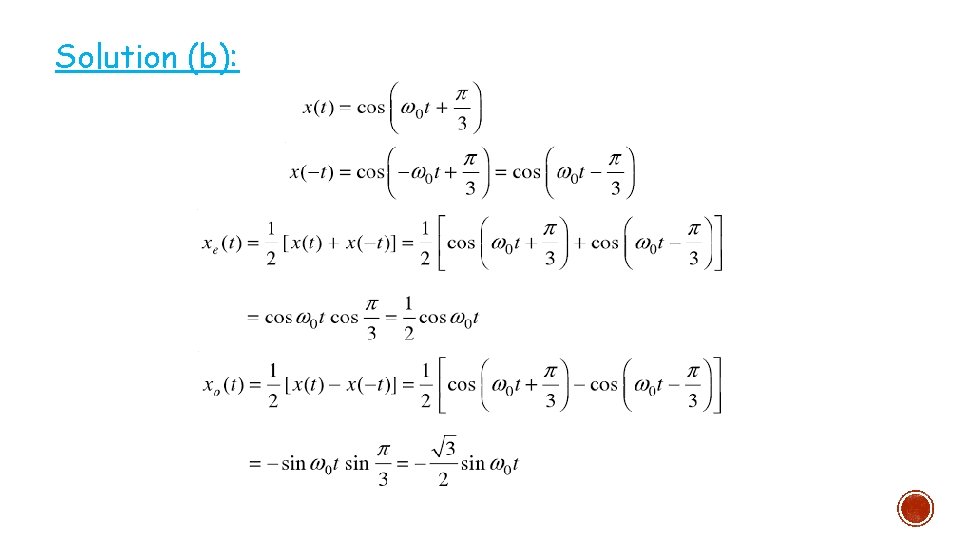
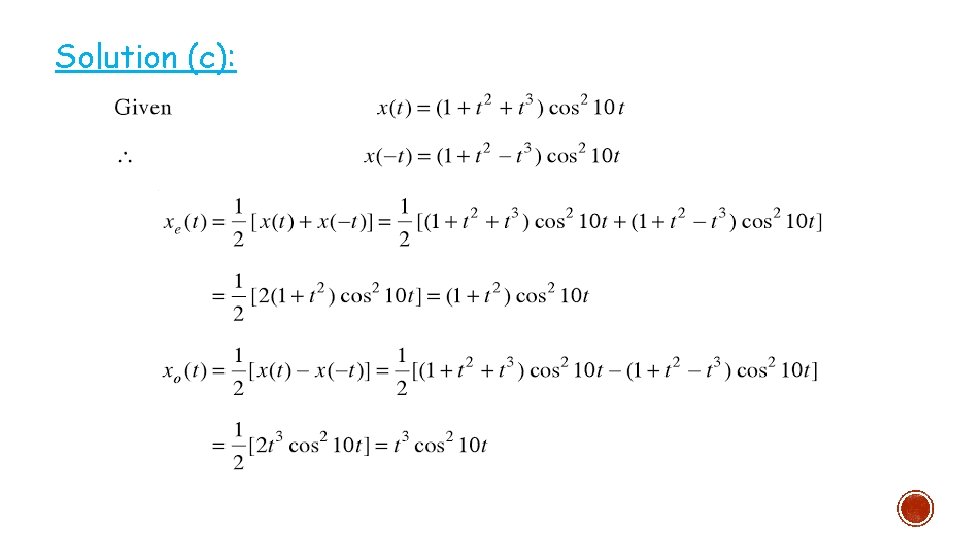















- Slides: 60

SIGNALS & SYSTEMS (ENT 281) Chapter 1: Signals & Systems Modeling Concepts DR. HASIMAH ALI SCHOOL OF MECHATRONIC ENGINEERING UNIVERSITY MALAYSIA PERLIS

Signals & Systems Modelling Concepts 1. 1 What Is a Signal? 1. 2 Classification of a Signals. 1. 2. 1 1. 2. 2 Continuous-Time and Discrete-Time Signals Even and Odd Signals. 1. 2. 3 Periodic and Non-periodic Signals. 1. 2. 4 Deterministic and Random Signals. 1. 2. 5 Energy and Power Signals. 1. 3 Basic Operation of the Signal. 1. 3. 1 Operations performed on dependent variables. 1. 3. 2 Operations performed on independent variables 1. 3. 3 Precedence Rule for Time Shifting and Time Scaling.

Signals & Systems Modelling Concepts 1. 1 What Is a Signal? 1. 2 Classification of a Signals. 1. 2. 1 1. 2. 2 Continuous-Time and Discrete-Time Signals Even and Odd Signals. 1. 2. 3 Periodic and Non-periodic Signals. 1. 2. 4 Deterministic and Random Signals. 1. 2. 5 Energy and Power Signals. 1. 3 Basic Operation of the Signal. 1. 3. 1 Operations performed on dependent variables. 1. 3. 2 Operations performed on independent variables 1. 3. 3 Precedence Rule for Time Shifting and Time Scaling.

1. 4 Elementary Signals. 1. 4. 1 Exponential Signals. 1. 4. 2 Sinusoidal Signal. 1. 4. 3 Sinusoidal and Complex Exponential Signals. 1. 4. 4 Exponential Damped Sinusoidal Signals. 1. 4. 5 Step Function. 1. 4. 6 Impulse Function. 1. 4. 7 Ramped Function. 1. 5 What is a System -System Block Diagram 1. 6 Properties of the System. 1. 6. 1 Stability. 1. 6. 2 Memory. 1. 6. 3 Causality. 1. 6. 4 Inevitability. 1. 6. 5 Time Invariance. 1. 6. 6 Linearity.

Objectives § The aim of this course is able to use mathematical techniques to help analyzing and synthesizing systems which process signals. § Engineers must model two distinct physical phenomena : i) Physical Systems – can be modeled by math equations. ii) Physical Signals – can be modeled by math functions.

What is Signals? A common form of human communication; i) use of speech signal; - face-to- face conservation or telephone channel. ii) use of visual; - signal taking the form of images of people or objects around us.

What is Signals? § Real-life example of signals; i) Doctor listening to the heartbeat, blood pressure and temperature of the patient. These indicate the state of health of the patient. ii) Daily fluctuations in the price of stock market will convey an information on the how the share for a company is doing. iii) Weather forecast over the radio provides information on the variation temperature, humidity, and the speed and direction of the prevailing wind.

§ By definition; signal is a function of one or more variable, which conveys information on the nature of a physical phenomenon. § A function of time representing a physical or mathematical quantities. - e. g. : Velocity, acceleration of a car, voltage/current of a circuit. § An example of signal; the electrical activity of the heart recorded with electrodes on the surface of the chest — the electrocardiogram (ECG or EKG) in the figure below. A short ECG registration of normal heart rhythm (sinus rhythm)

Signals, Systems And Their Applications § Concepts arise and use in various fields; 1)Communication 7) Energy generation & distribution 2) Aeronautics & astronautics 8) Chemical process control 3) Circuit Design 9) Speech processing 4) Acoustics 5) Seismology 6) Biomedical engineering 10) Image processing 11) Economic & Financial Forecasting 12) Weather forecasting & etc…. .

Two Basic Features In Common; § Signals are function of independent variables. § System response to input signals by producing other signals. § A function of one or more variable, which conveys information on the nature of a physical phenomenon. § A function of time representing a physical or mathematical quantities. § Example: voltage & current are signals. Circuits are systems.

First Example § Automobile driver depresses the accelerator pedal. § The automobile responses by increasing the speed of the vehicle. § System is the automobile, pressure on pedal is the input signal, the automobile speed is the response or output signal. Second Example § Control input signal to a robot arm. § The robot responses by producing movement of the arm. § System is the robot arm, control electrical signal is the input signal, the movement of the arm is the response or output signal. Input signal System Output signal

Applications Objectives § When presented with a specific system, we are interested in characterizing it in detail to understand how it will response to input signals. § Examples: Understanding of human auditory system; Vocal Tract System; Economic system; Analysis of circuits; Determination of aircraft response characteristic due to pilot commands & wind gusts.

1. 2 Classification Of A Signal Ø 5 methods of classifying signals, based on different features, are common; 1. 2. 1 Continuous-Time and Discrete-Time Signals 1. 2. 2 Even and Odd Signals. 1. 2. 3 Periodic and Non-periodic Signals. 1. 2. 4 Deterministic and Random Signals. 1. 2. 5 Energy and Power Signals.

1. 2. 1 Continuous-time And Discrete-time. § Two types of signals are present naturally. i) Continuous-Time - Signals varying continuously with time or some other variable, e. g. space or distance. • Defined for all values of time • Also called analog signal

1. 2. 1 Continuous-time And Discrete-time. ii) Discrete-Time - Signals that exist only at discrete point of time, e. g. daily closing stock market average or index. • Defined at only certain instants of time. ØContinuous signal can be converted into a sequence of numbers (discrete signal) by sampling. Continuous signal Sampling Discrete signal

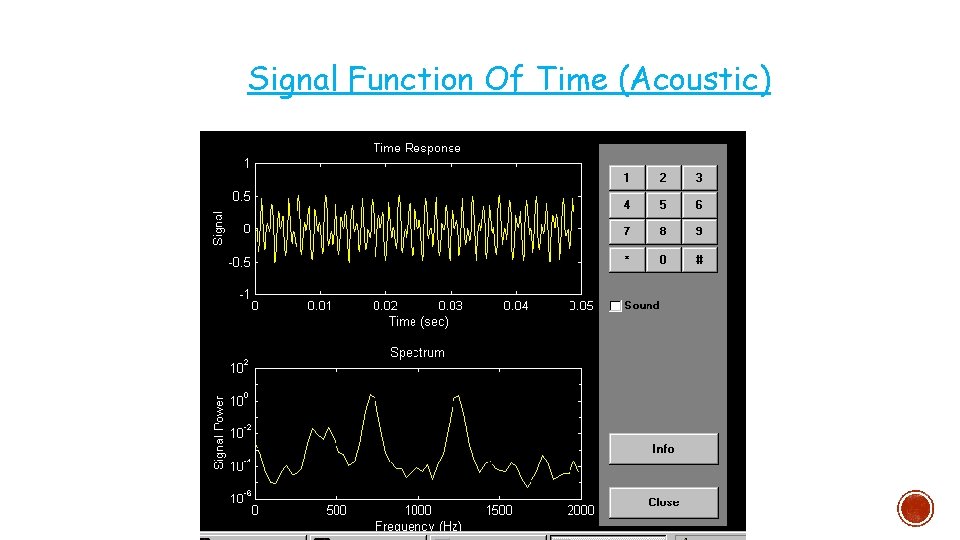
Continuous Time Signals (CTS) § functions whose amplitude, x(t) or value varies continuously with time, t. § A signal x(t) is said to be a continuous- time signal if it is defined for all time t. § E. g. ; speed of car, smell or odor or acoustic wave is converted into an electrical signal; and microphone, which converts variations in sound pressure into corresponding variations in voltage and current.

Signal Function Of Time (Acoustic)

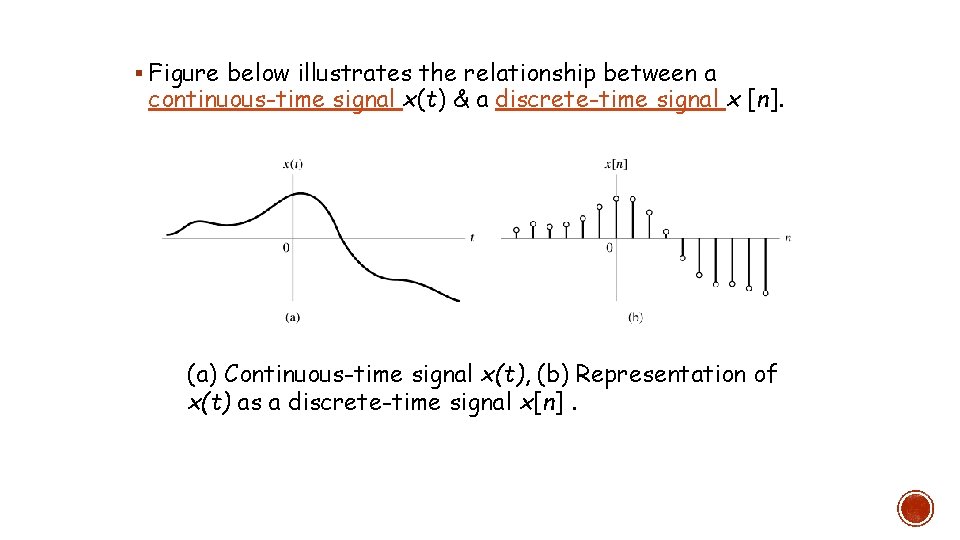
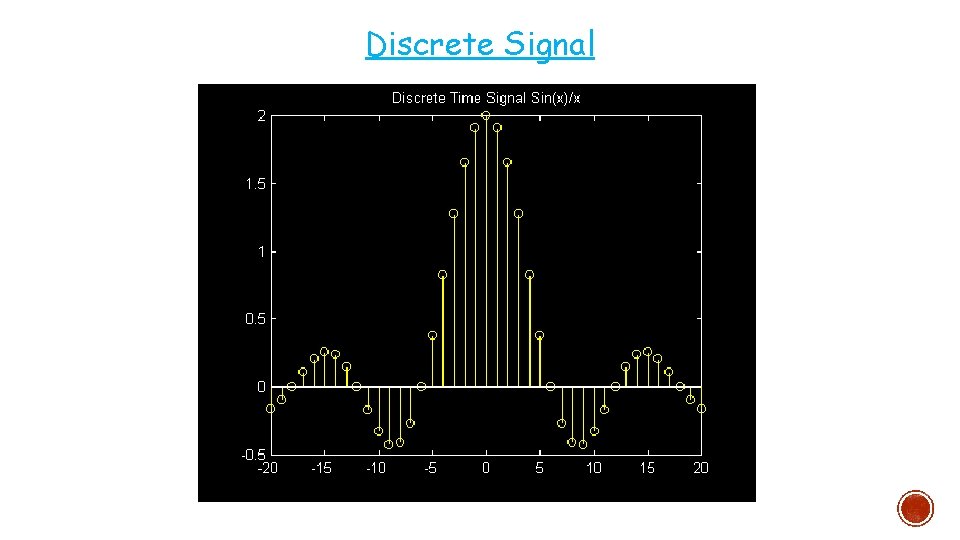
Discrete-time Signals (DTS) § Discrete-Time Signal are function of discrete variable, i. e, defined only at discrete instants of time. § It is often derived from continuous-time signal by sampling at uniform rate. § Let Ts denotes sampling period; n denotes integer (+ve & -ve values) § The symbol n denotes time for discrete time signal [. ] & is used to denote discrete-value quantities. § Sampling a continuous-time signal x(t) at time t = n. Ts yields a sample with the value x (n. Ts ). § ~ represented by the sequence of no. …, x [-2], x [-1], x [0], x [1], x [2], …, which can take on a continuum values.

§ Figure below illustrates the relationship between a continuous-time signal x(t) & a discrete-time signal x [n]. (a) Continuous-time signal x(t), (b) Representation of x(t) as a discrete-time signal x[n].

Discrete Signal

1. 2. 2 Even And Odd Signals Even (Symmetric) Signal § A continuous –time signal x(t) is said to be an even signal if x(-t) = x(t) for all t § A discrete-time signal x(n) is said to be an even (symmetric) signal if x(n) = x(-n) for all n § Even signals are symmetrical about the vertical axis or time axis. Hence they are also called symmetric signal. E. g. cosine wave.

1. 2. 2 Even And Odd Signals Odd (antisymmetric) Signal § A continuous –time signal x(t) is said to be an odd (antisymmetric) signal if x(-t) = -x(t) for all t § A discrete-time signal x(n) is said to be an odd (antisymmetric) signal if x(n) = -x(n) for all n § Odd signals are antisymmetrical about the time origin. Hence they are also called antisymmetric signal. E. g. Sine wave.

1. 2. 2 Even And Odd Signals § Solving for xe(t) and xo(t), we thus obtain,

1. 2. 2 Even And Odd Signals § The product of two even or odd signals is an even signal, § The product of even signal and odd signal is an odd signal. § Prove: If x 1(t) and x 2(t) are both even, i. e

1. 2. 2 Even And Odd Signals § The product of two even or odd signals is an even signal, § The product of even signal and odd signal is an odd signal. § Prove: If x 1(t) and x 2(t) are both odd, i. e

1. 2. 2 Even And Odd Signals § The product of two even or odd signals is an even signal, § The product of even signal and odd signal is an odd signal. § Prove: If x 1(t) is even and x 2(t) is odd, i. e

1. 2. 2 Even And Odd Signals

Example 1: §
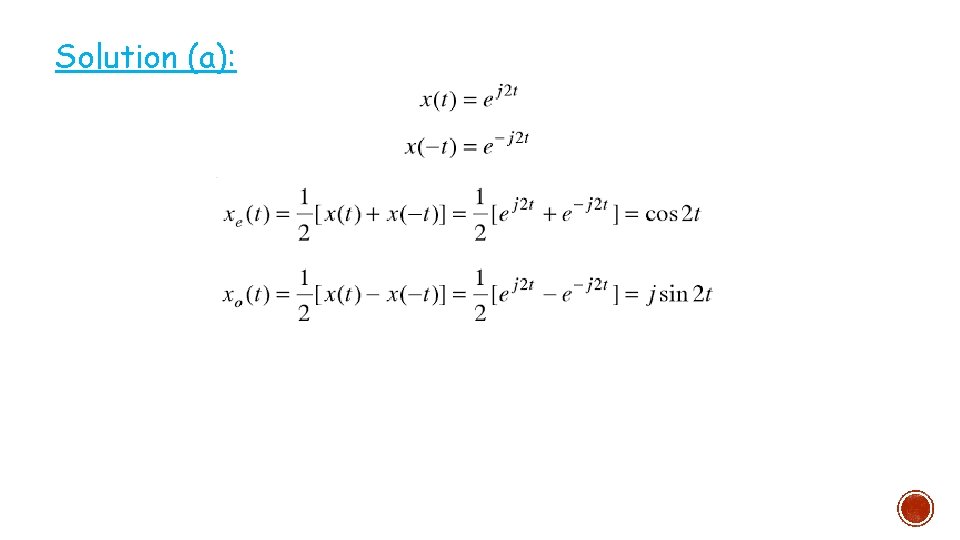
Solution (a):
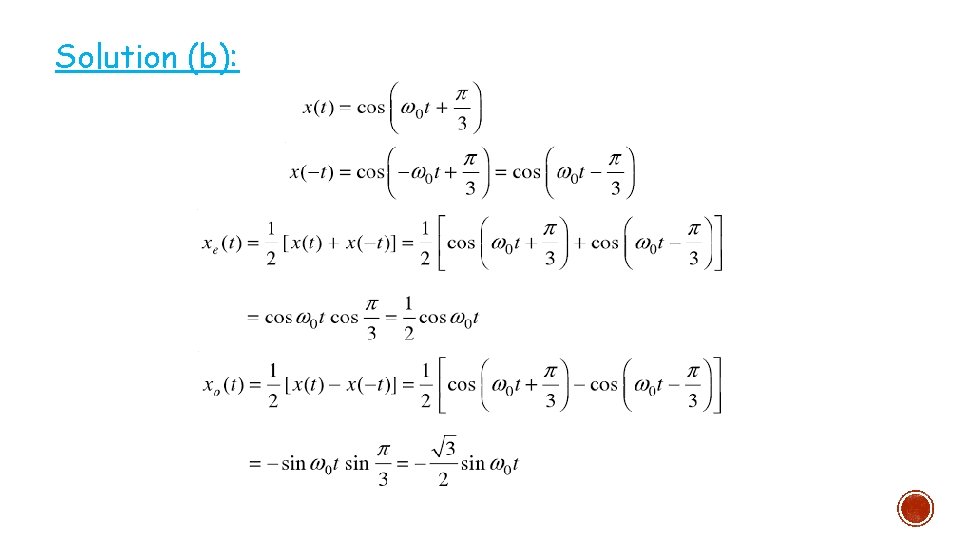
Solution (b):
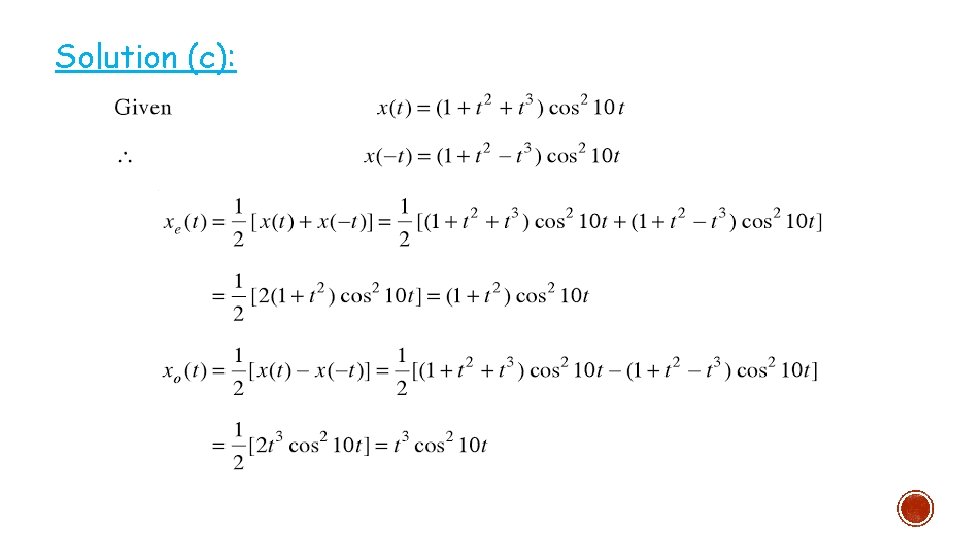
Solution (c):

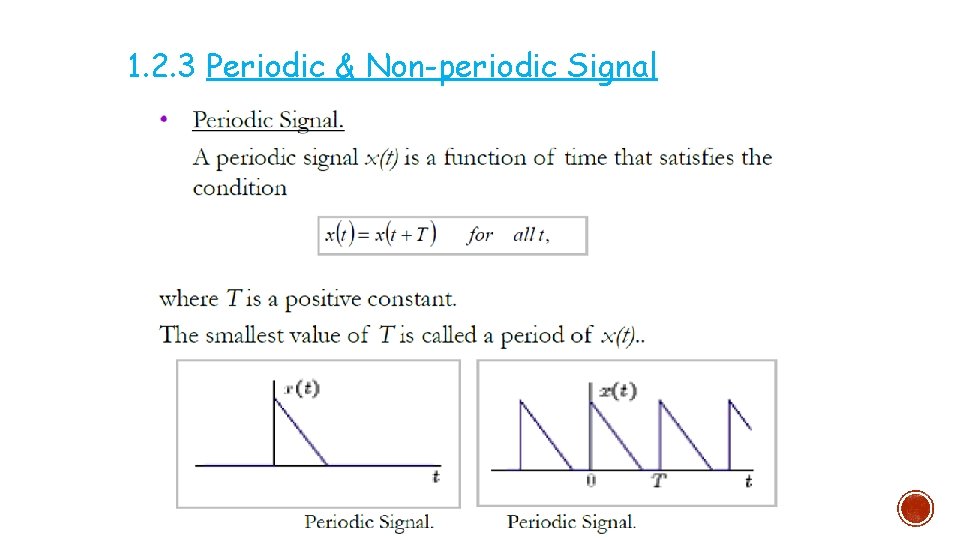
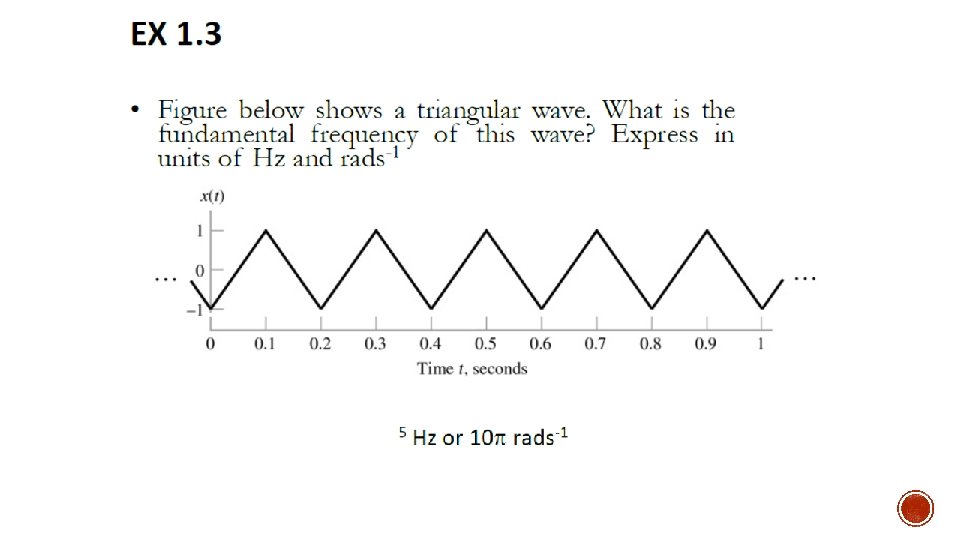
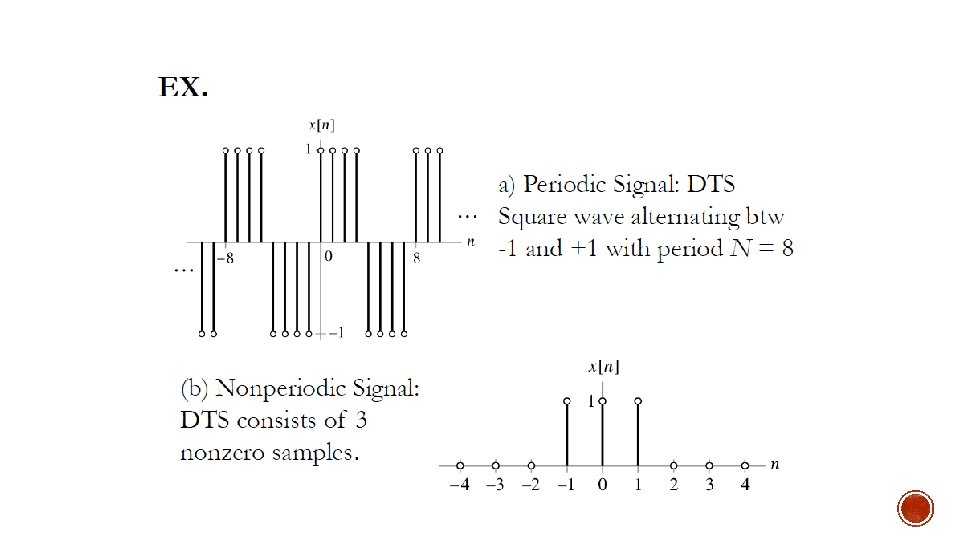
1. 2. 3 Periodic & Non-periodic Signal §

1. 2. 3 Periodic & Non-periodic Signal






EX. 1. 4 §


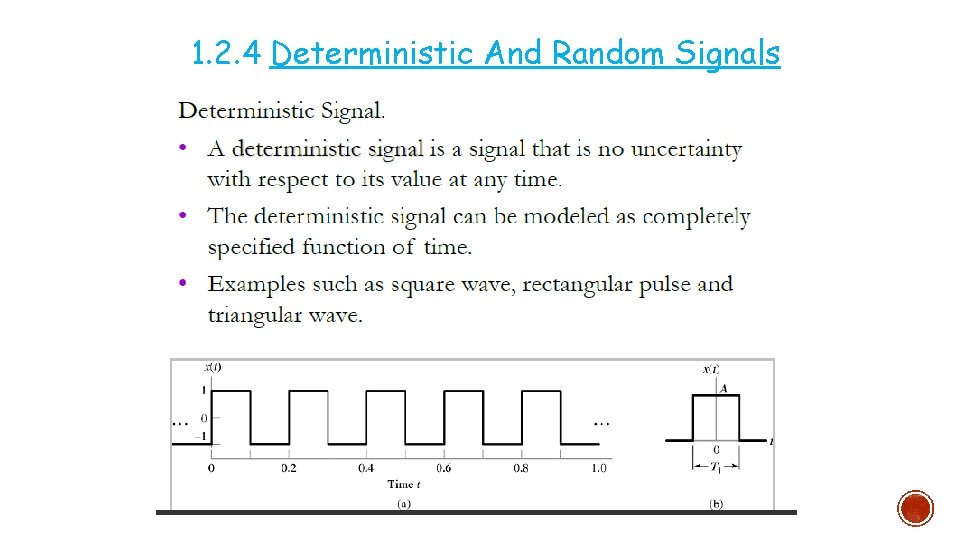
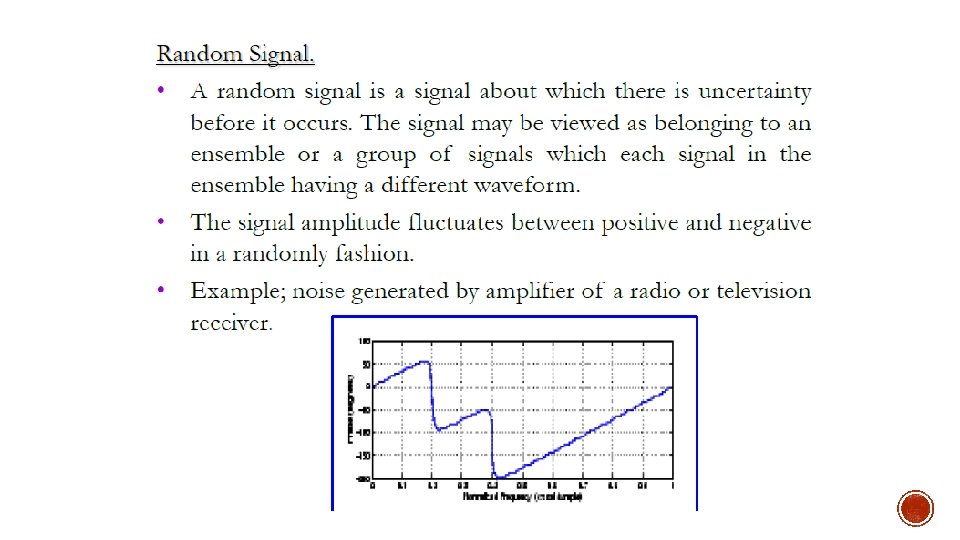
1. 2. 4 Deterministic And Random Signals


1. 2. 5 Energy Signal And Power Signals

1. 2. 5 Energy Signal And Power Signals


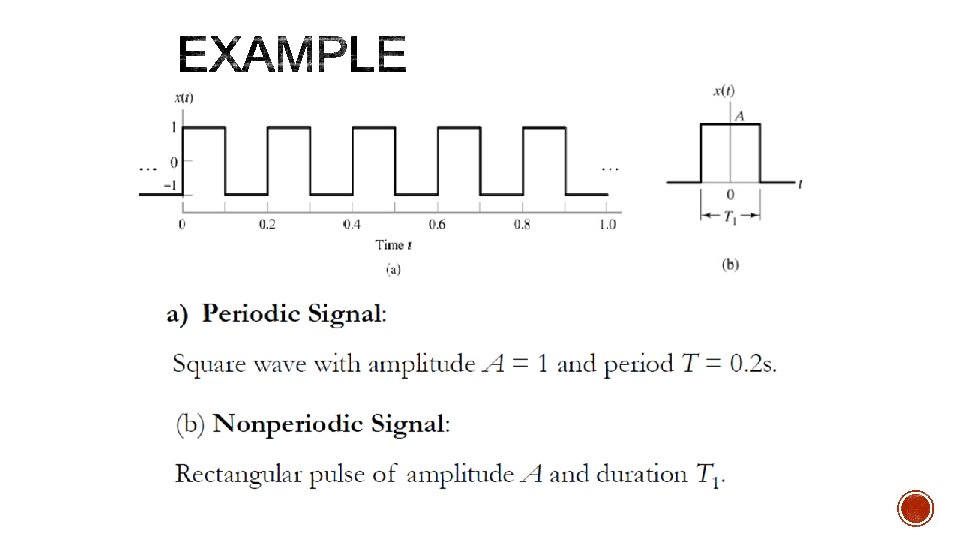
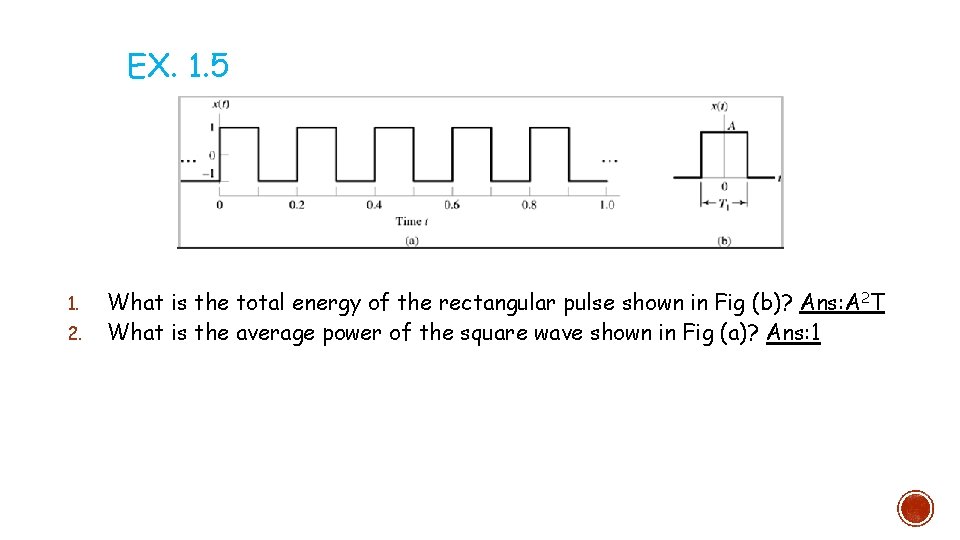
EX. 1. 5 1. 2. What is the total energy of the rectangular pulse shown in Fig (b)? Ans: A 2 T What is the average power of the square wave shown in Fig (a)? Ans: 1

Basic Operations on Signals Systems are used to process or manipulate signals which could involve a combination of some basic operations. § Operations performed on dependents variables § Operations performed on independent variables § Precedence Rule for Time Shifting and Time Scaling

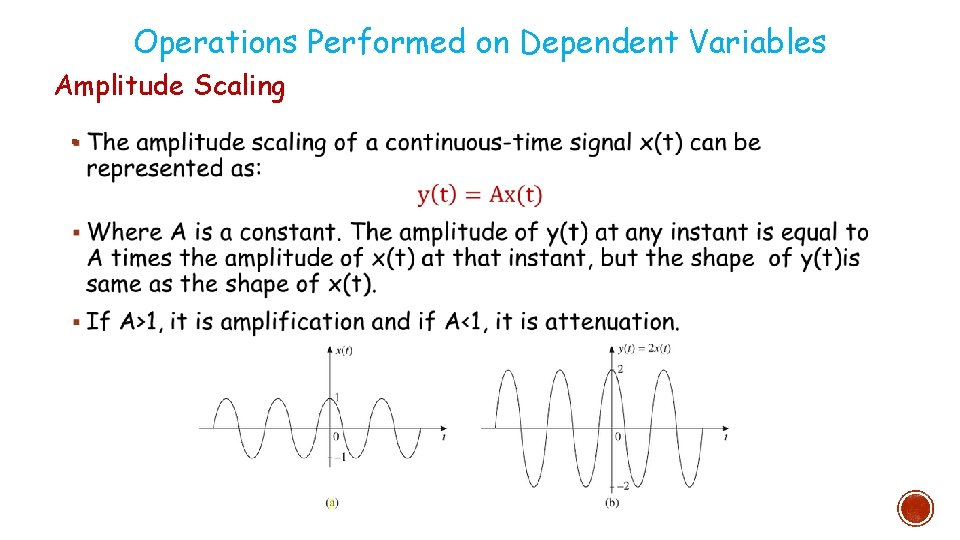
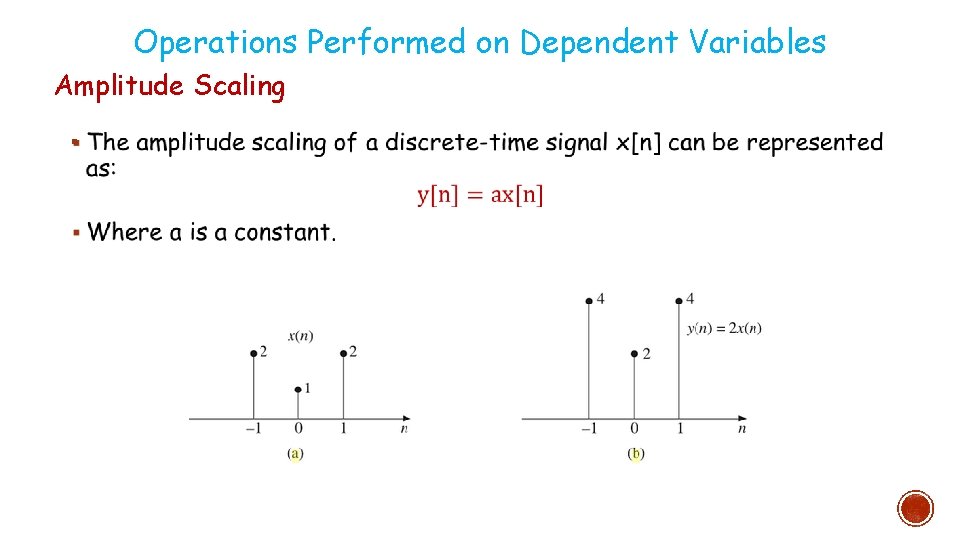
Operations Performed on Dependent Variables Amplitude Scaling §

Operations Performed on Dependent Variables Amplitude Scaling §

Operations Performed on Dependent Variables Signal Addition §

Operations Performed on Dependent Variables Signal Multiplication §

Operations Performed on Dependent Variables Differentiation § Integration

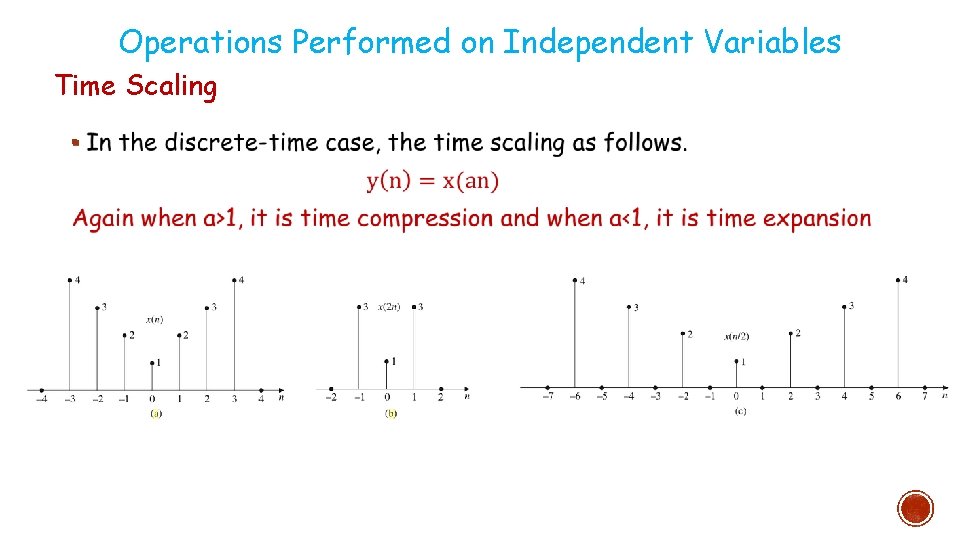
Operations Performed on Independent Variables Time Scaling §

Operations Performed on Independent Variables Time Scaling §

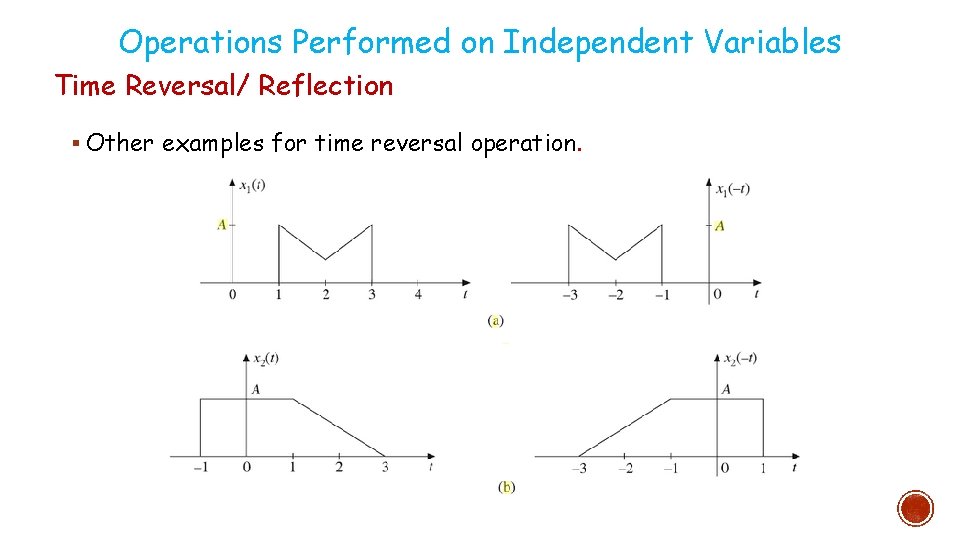
Operations Performed on Independent Variables Time Reversal/ Reflection §

Operations Performed on Independent Variables Time Reversal/ Reflection § Other examples for time reversal operation.

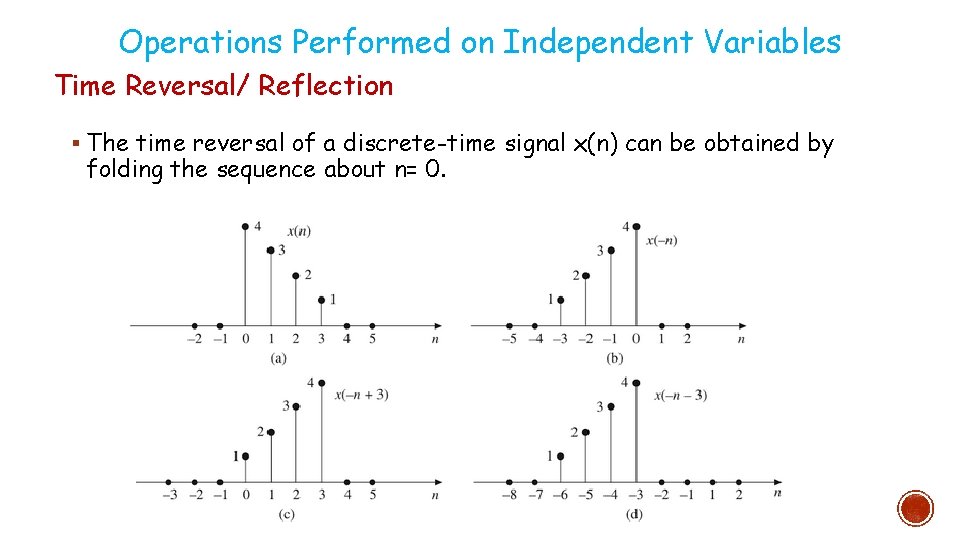
Operations Performed on Independent Variables Time Reversal/ Reflection § The time reversal of a discrete-time signal x(n) can be obtained by folding the sequence about n= 0.

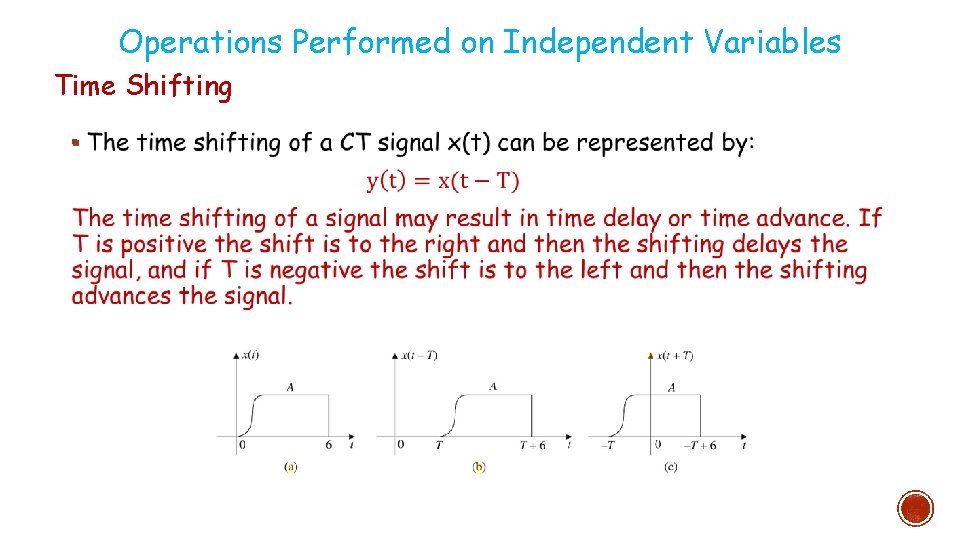
Operations Performed on Independent Variables Time Shifting §

Operations Performed on Independent Variables Time Shifting §

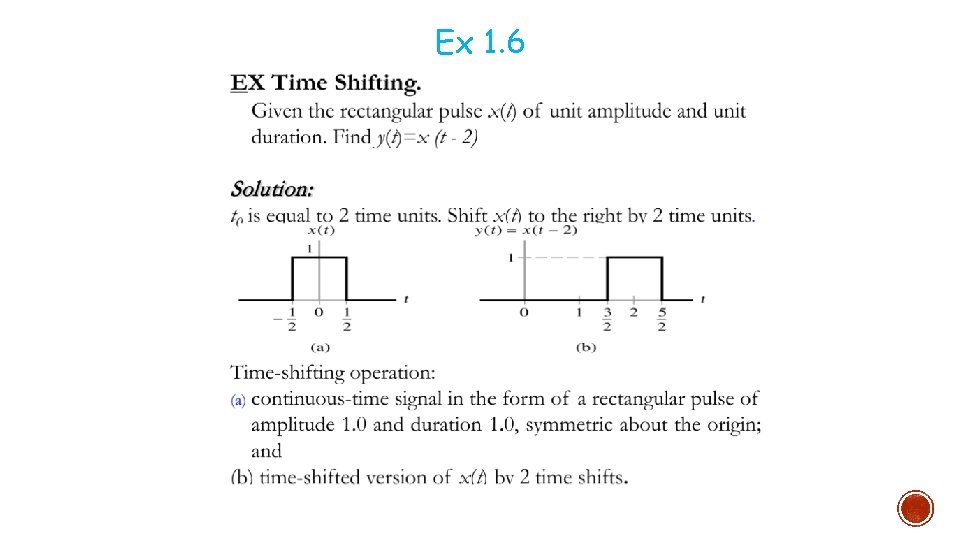
Ex 1. 6