Signals and Systems Presented by M N Narsaiah

Signals and Systems Presented by M. N. Narsaiah Head – IQAC Associate Professor, ECE Department 1

Introduction to Signals and Systems Signal : A signal is defined as a time varying physical phenomenon which is intended to convey information. (or) Signal is a function of time. (or) Signal is a function of one or more independent variables, which contain some information. Example: voice signal, video signal, signals on telephone wires , EEG, ECG etc. Signals and Systems Quality Audit in Academics Signals may be of continuous time or discrete time signals. System : System is a device or combination of devices, which can operate on signals and produces corresponding response. Input to a system is called as excitation and output from it is called as response. For one or more inputs, the system can have one or more outputs. 2
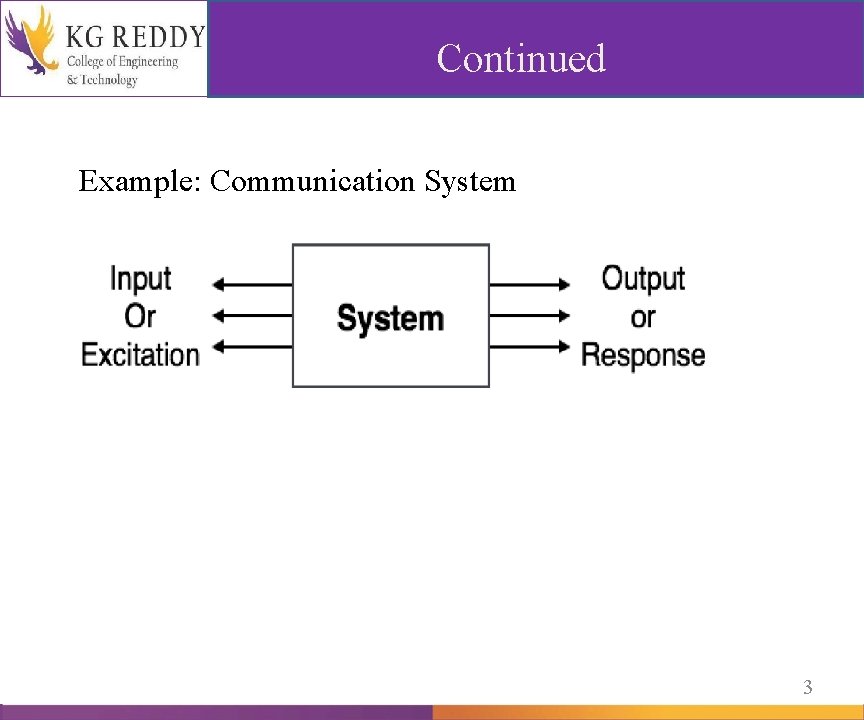
Continued Example: Communication System 3

Elementary signals or Basic signals 1. Unit Step Function 2. Unit Impulse Function 3. Unit Ramp signal 4. Unit Parabolic signal 5. Signum function 5. Real Exponential signal 7. Rectangular signal 8. Triangular signal 9. Sinusoidal Signal 10. Sinc Function 11. Sampling Function 4

Unit step signal 1. It is used as best test signal. 2. Area under unit step function is unity. Unit step signal 5

Unit Impulse Function 6
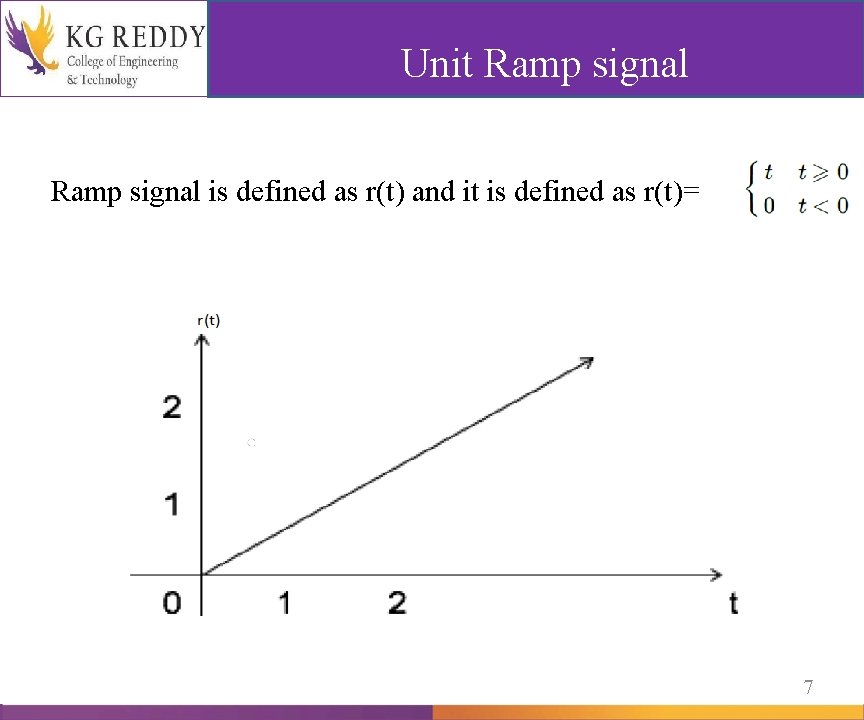
Unit Ramp signal is defined as r(t) and it is defined as r(t)= 7

Unit Parabolic signal 8

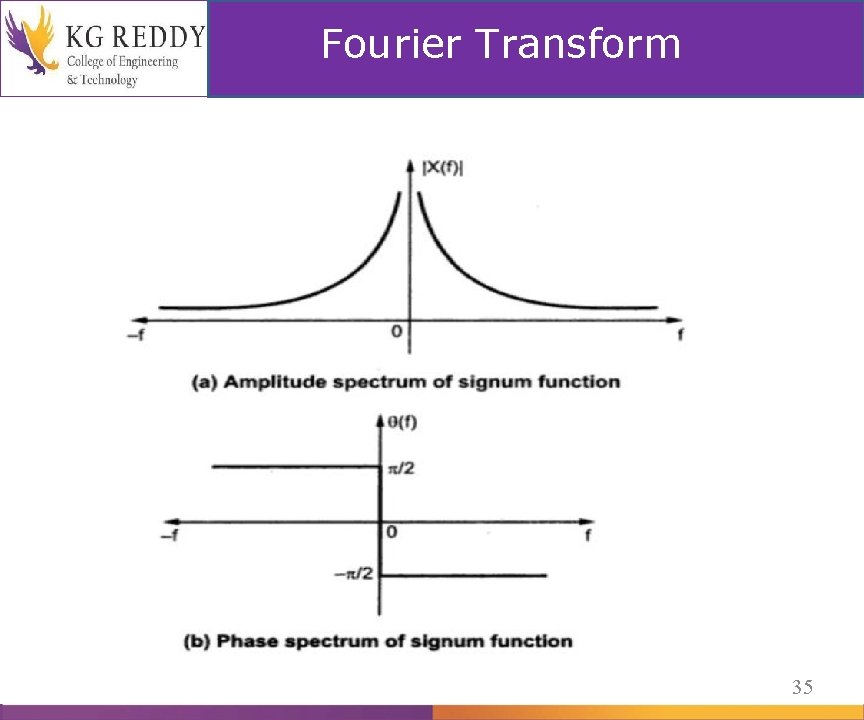
sgnt = 2 u(t) – 1 Signum function is denoted as sgn (t) and defined as Sgn (t) = Note : Sgn (t) = 2 u(t) – 1 9

Real Exponential signal is in the form of x(t) = The shape of exponential can be defined by α. l Exponential signal 10
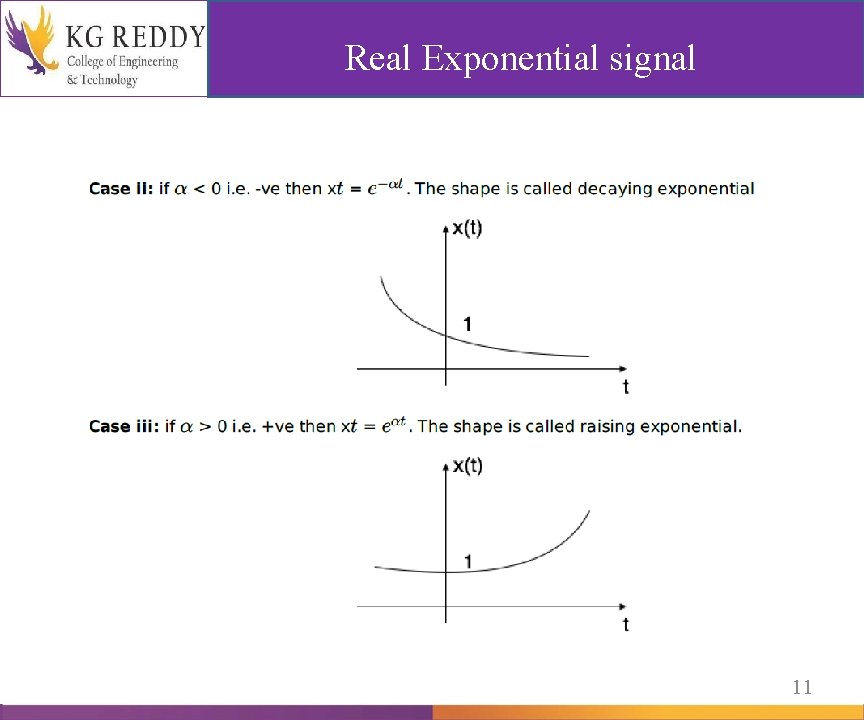
Real Exponential signal 11
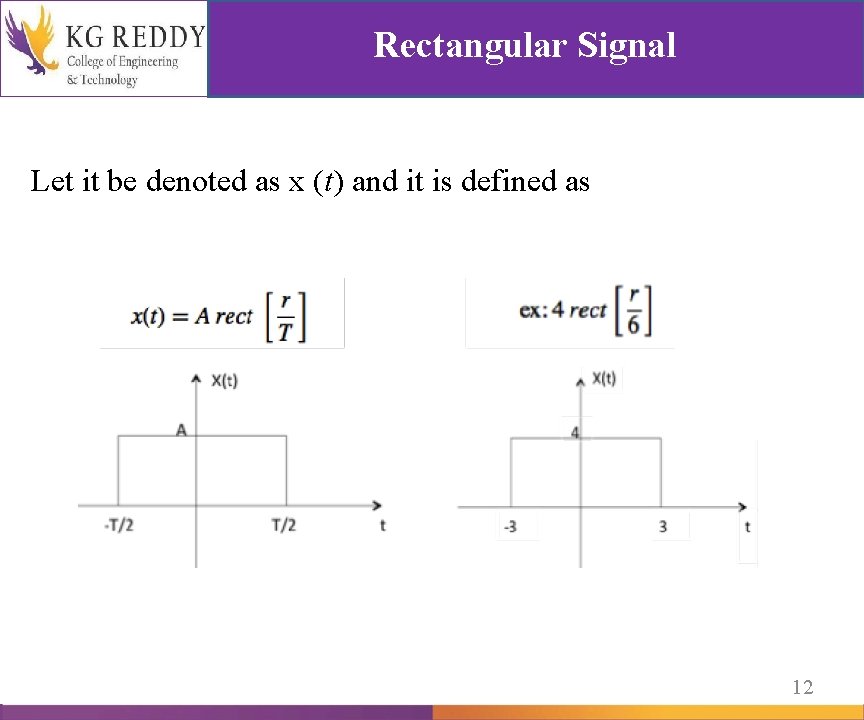
Rectangular Signal Let it be denoted as x (t) and it is defined as 12

Triangular Signal • Let it be denoted as x(t) 13
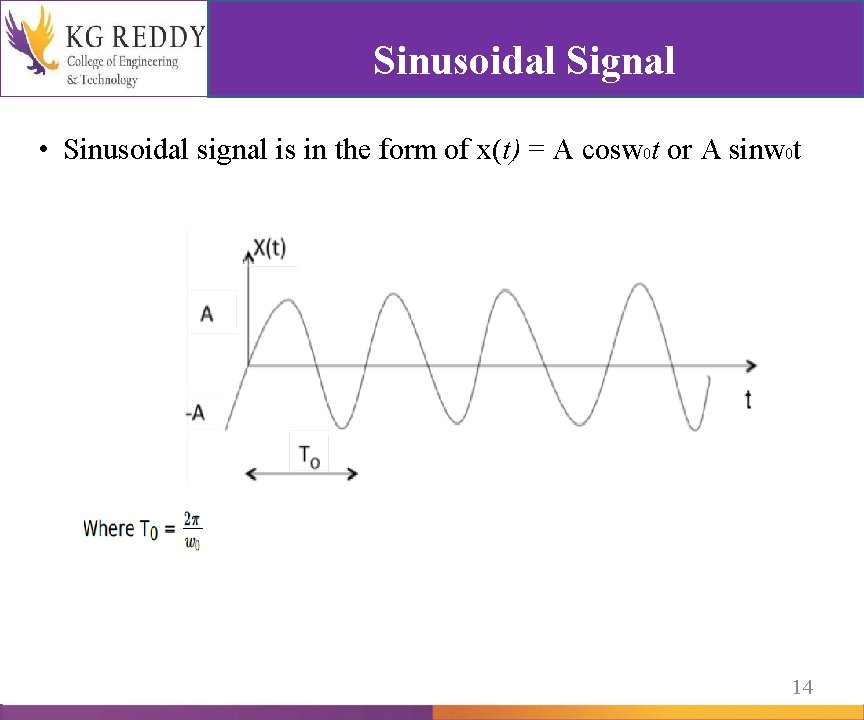
Sinusoidal Signal • Sinusoidal signal is in the form of x(t) = A cosw 0 t or A sinw 0 t 14
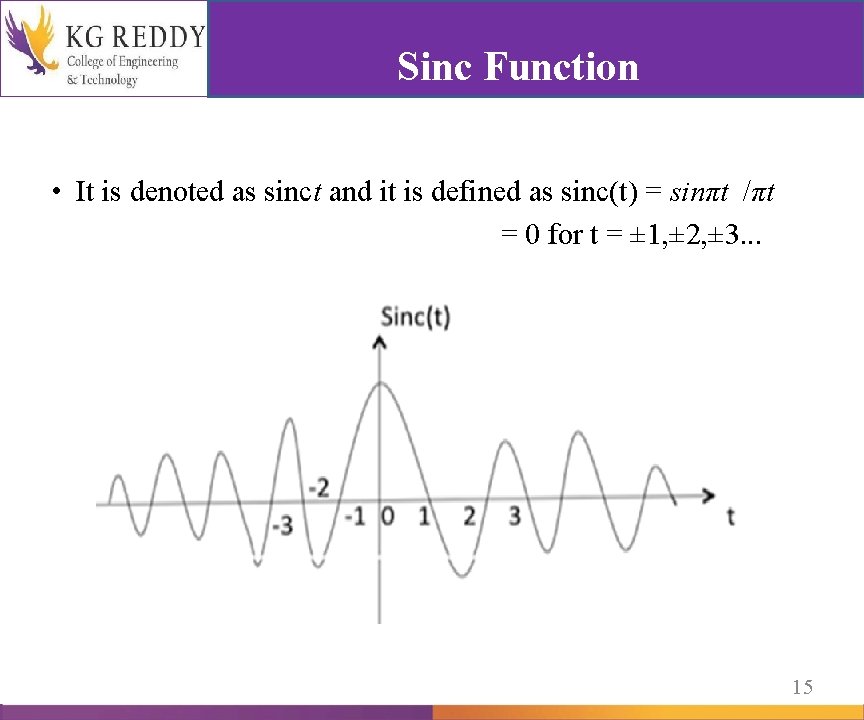
Sinc Function • It is denoted as sinct and it is defined as sinc(t) = sinπt /πt = 0 for t = ± 1, ± 2, ± 3. . . 15
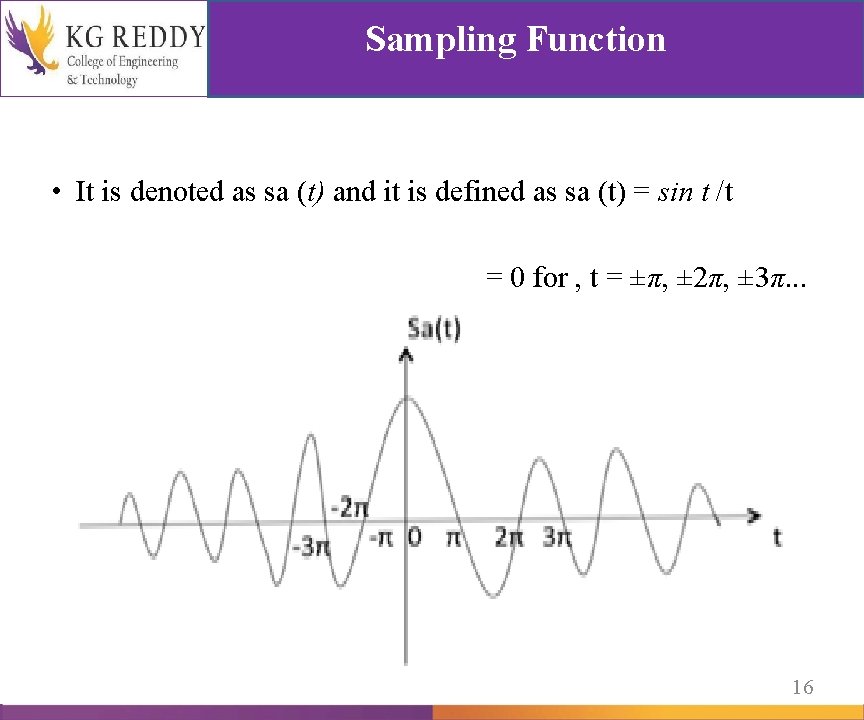
Sampling Function • It is denoted as sa (t) and it is defined as sa (t) = sin t /t = 0 for , t = ±π, ± 2π, ± 3π. . . 16

Operation on signals • Operation on signals can be two types : I Operation on dependent variables 1. Addition/Subtraction 2. Multiplication 3. Amplitude scaling II. Operation on independent variables 1. Time reversal 2. Time shifting 3. Time scaling 17

Classification of signals • Signals are classified into the following categories: 1. Continuous Time and Discrete Time Signals 2. Analog and digital signals 3. Deterministic and Non-deterministic Signals 4. Even and Odd Signals 5. Periodic and A periodic Signal 6. Energy and Power Signals 7. Causal and Non-causal signals 18

Classification of systems • Systems are classified into the following categories: 1. Liner and Non-liner Systems 2. Time Variant and Time Invariant Systems 3. Liner Time variant and Liner Time invariant systems 4. Static and Dynamic Systems 5. Causal and Non-causal Systems 6. Invertible and Non-Invertible Systems 7. Stable and Unstable Systems 19

Thank you Any questions ? 20

Signals and Systems Presented by M. N. Narsaiah Head – IQAC Associate Professor, ECE Department 1

Introduction to Fourier Analysis Fourier analysis can be two types: 1. Fourier Series 2. Fourier Transform Fourier Series: • The representation of signals over a certain interval of time in terms linear combination of orthogonal functions is called Fourier Series • Fourier series is applicable only for periodic signals • Different forms of Fourier Series 1. Trigonometric form 2. Cosine form or polar form 3. Exponential form 22

Fourier Transform (FT) Fourier Transform: • Fourier transform converts a time domain signal to frequency domain signal • Can a periodic signals be analyzed in terms of frequency components? • Yes, and the Fourier transform is a tool for this analysis • It is applicable for periodic and non- periodic signals • The major difference w. r. t. the line spectra of periodic signals is that the spectra of a periodic signals are defined for all real values of the frequency variable not just for a discrete set of values 23

Fourier Transform Given a signal x(t), its Fourier transform is defined as Fourier transform A signal x(t) is said to have a Fourier transform in the ordinary sense if the above integral converges 24

Fourier Transform The integral does converge if 1. the signal x(t) is “well-behaved” 2. and x(t) is absolutely integrable, namely, Note: well behaved means that the signal has a finite number of behaved discontinuities, maxima, and minima within any finite time interval 25

Inverse Fourier Transform Given a signal x(t) with Fourier transform , x(t) can be recomputed from by applying the inverse Fourier transform given by transform Fourier transform pair 26

Example: Fourier transform of a DC or Constant Signal Consider the signal clearly x(t) does not satisfy the first requirement since Therefore, the constant signal does not have a Fourier transform in the ordinary sense Later on we’ll see that it has however a Fourier transform in a generalized sense 27
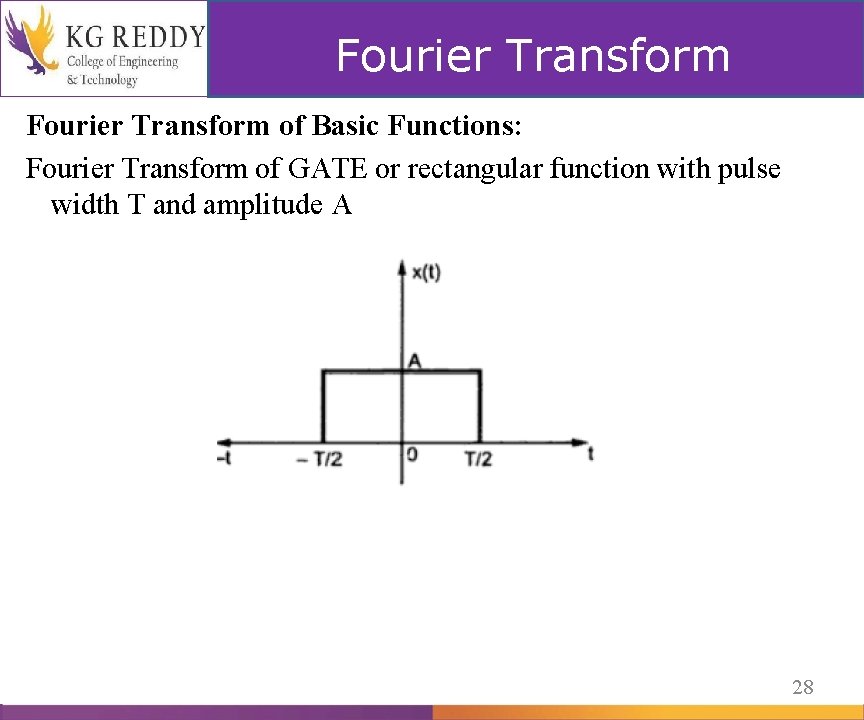
Fourier Transform of Basic Functions: Fourier Transform of GATE or rectangular function with pulse width T and amplitude A 28

29
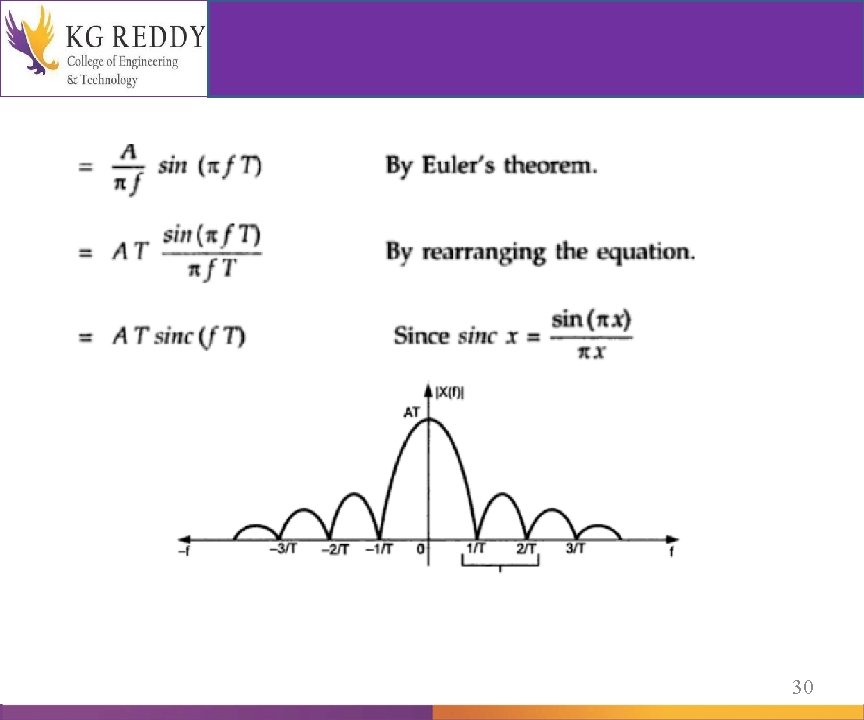
30

Fourier Transform • Fourier Transform of Impulse Function 31

32
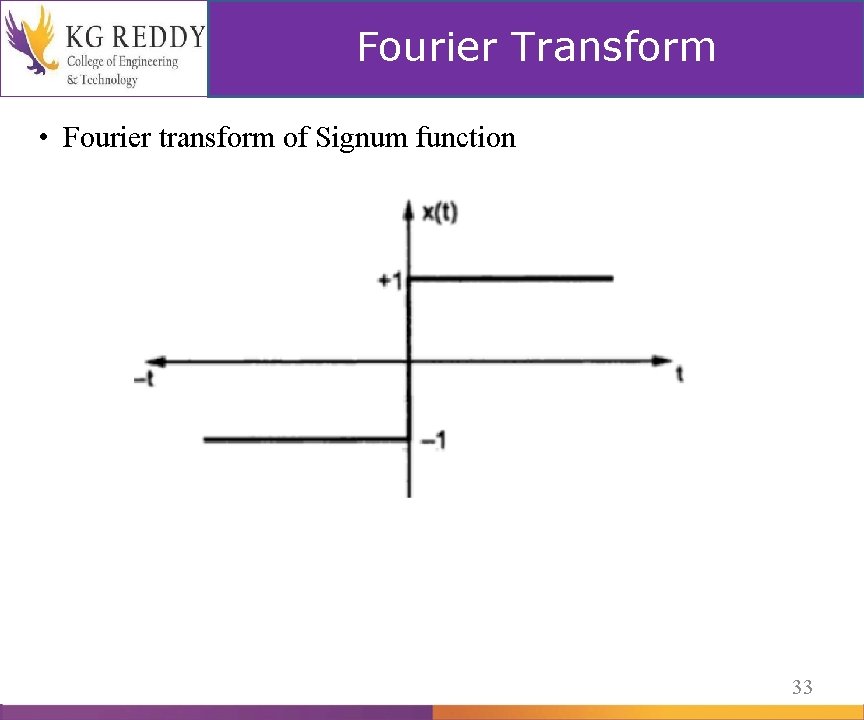
Fourier Transform • Fourier transform of Signum function Fourier Transform 33

Fourier Transform 34
Fourier Transform 35
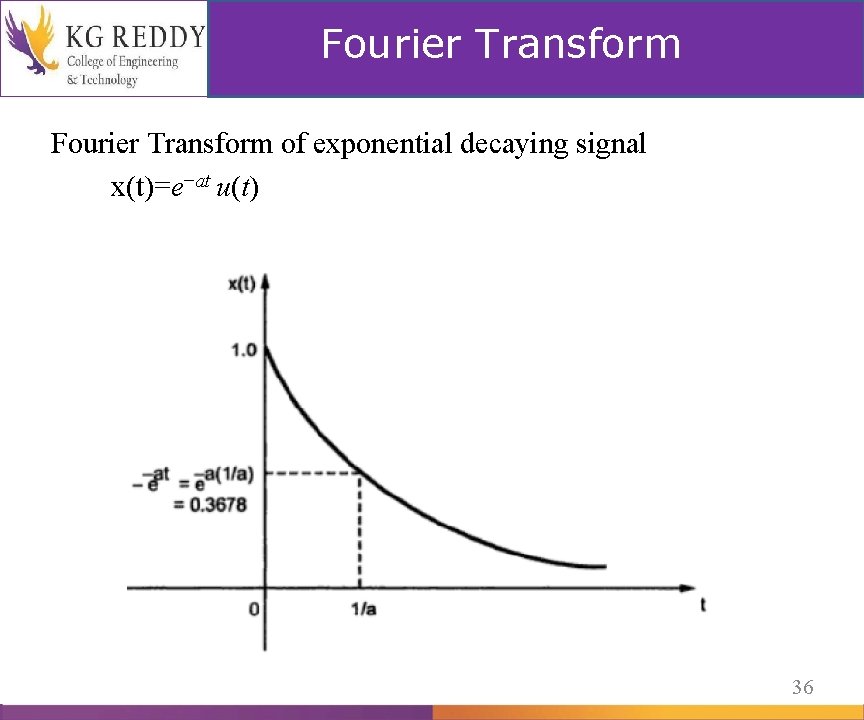
Fourier Transform of exponential decaying signal x(t)=e−at u(t) 36

Fourier Transform of exponential decaying signal x(t)=e−at u(t) 37

Properties of Fourier Transform 1. 2. 3. 4. 5. 6. 7. 8. Linearity Duality Time shifting Frequency shifting or modulation property Time scaling Area under curves x(t) and X(f) Time differentiation and integration Convolution 38

Linearity 39

Duality 40

Time shifting f Fourier Transform 41

Frequency shifting or Modulation property 42

Time scaling n 43

Area under curves x(t) and X(f) If x(t) �X(f) � X(0) x(0) � 44

Time differentiation 45

Time Integration 46

Frequency differentiation 47

Convolution 48

Convolution 49

Parseval’ s Theorem 50

Parseval’s Theorem Let x(t) be a periodic signal with period T The average power P of the signal is defined as Expressing the signal as it is also 51

Fourier Series: • The representation of signals over a certain interval of time in terms linear combination of orthogonal functions is called Fourier Series • Fourier series is applicable only for periodic signals • Different forms of Fourier Series 1. Trigonometric form 2. Cosine form or polar form 3. Exponential form 52

Dirichlet Conditions • A periodic signal x(t), has a Fourier series if it satisfies the following conditions: 1. x(t) is absolutely integrable over any period, namely 2. x(t) has only a finite number of maxima and minima over any period 3. x(t) has only a finite number of discontinuities over any period 53

Fourier Series Any periodic signal x(t) can be expressed in Trigonometric form of Fourier series given by 54

Fourier Series Any periodic signal x(t) can be expressed in Compact form of Fourier series which also known as Polar form is given by 55

Fourier Series Any periodic signal x(t) can be expressed in Exponential form of Fourier series given by 56

Symmetric properties of Fourier Series If the periodic signal x(t) has some type of symmetry, then some of the trigonometric Fourier series coefficients may became zero and calculations of the coefficients becomes easy. There are four types of symmetric properties 1. 2. 3. 4. Even symmetry or Mirror symmetry Odd symmetry or Rotation symmetry Half-wave symmetry Quarter wave symmetry 57

Symmetric properties of Fourier Series Even symmetry: A signal x(t) which satisfy the following condition is said to have even symmetry x(-t) = x(t) a 0 = ( ) a n = ( ) b n = 0 Note: Fourier series expansion of even periodic function contains only cosine terms and constant 58

Symmetric properties of Fourier Series Odd symmetry: A signal x(t) which satisfy the following condition is said to have odd symmetry x(-t) = - x(t) a 0 = 0 a n = 0 b n= ( ) Note: Fourier series expansion of odd periodic function contains only sine terms. 59

Symmetric properties of Fourier Series Half-Wave symmetry: A signal x(t) which satisfy the following condition is said to have-wave symmetry x(t) = - x(t ± T/2 ) a 0 = 0 a n = 0 b n= 0 When n is even a n = ( ) b n= ( ) When n is odd Note: Fourier series expansion of function with have wave symmetry contains only odd harmonics terms. 60

Symmetric properties of Fourier Series Quarter-Wave symmetry: A signal x(t) which satisfy the following condition is said to Quarter-wave symmetry x(t) = - x(t ± T/4 ) Case i : A signal which has either even symmetry or odd symmetry along with the half-wave symmetry is said to have Quarter-Wave symmetry Even symmetry Have-wave symmetry a 0 = 0 a 0 = ( ) a n = 0 a n = ( ) b n = 0 When n is even b n = 0 a n = ( ) b n= ( ) When n is odd a 0 = 0 a n = ( ) Over all coefficients b n = 0 61

Symmetric properties of Fourier Series Quarter-Wave symmetry: A signal x(t) which satisfy the following condition is said to Quarter-wave symmetry x(t) = - x(t + or –T/4 ) Case i: A signal which has either even symmetry or odd symmetry along with the half-wave symmetry is said to have Quarter-Wave symmetry Odd symmetry Have-wave symmetry a 0 = 0 a n = 0 b n = 0 When n is even b n = ( ) a n = ( ) b n= ( ) When n is odd a 0 = 0 a n = 0 Over all coefficients b n = ( ) 62

Properties of the Fourier Transform - Summary 63

Common Fourier Transform Pairs 64

Presented by M. N. Narsaiah Head – IQAC Associate Professor, ECE Department 1

Linear Time Invariant(LTI) Systems • A system satisfying both the linearity and the timeinvariance property • LTI systems are mathematically easy to analyze and characterize, and consequently, easy to design. Signals and Systems Quality Audit in Academics • Highly useful signal processing algorithms have been developed utilizing this class of systems over the last several decades. • They possess superposition theorem. 66

Convolution: Convolution is a mathematical operation used to express the relation between input and output of an LTI system. It relates input, output and impulse response of an LTI system as y(t) = x(t) ∗ h(t) Where y (t) = output of LTI x (t) = input of LTI h (t) = impulse response of LTI There are two types of convolutions: 1. Continuous convolution 2. Discrete convolution 67

Continuous Convolution 68

Discrete Convolution Y (n) = x(n) ∗ h(n) By using convolution we can find zero state response of the system. 69

Convolution sum/ Superposition sum The discrete time unit impulse response and the convolution sum representation of LTI systems • The last equation is called superposition sum or the convolution sum. Operation on the right hand side is known as convolution of the sequence x[n] and h[n]. • We will represent the operation of the convolution symbolically y[n] = x[n] * h[n] • LTI system is completely characterized by its response to a single signal namely its response to the unit impulse. 70

Properties of Convolution 5. Convolution with Impulse x 1 (t) ∗ δ(t) = x(t) x 1 (t) ∗ δ(t − t 0 ) = x(t − t 0 ) 6. Convolution of Unit Steps u(t) ∗ u(t) = r(t) u (t − T 1 ) ∗ u(t − T 2 ) = r(t − T 1 − T 2 ) u(n) ∗ u(n) = [n + 1]u(n) 7. Scaling Property 8. Differentiation of Output 71

Properties of Convolution 8. Differentiation of Output Note: Convolution of two causal sequences is causal. Convolution of two anti causal sequences is anti causal. Convolution of two unequal length rectangles results a trapezium. Convolution of two equal length rectangles results a triangle. 72

Convolution sum representation of LTI system 73
![Example of Convolution y(0)=x(0)h(0) y(1)=x(0)h(1) h(1 -k)=h[-(k-1)] h(2 -k)=h[-(k-2)] +x(1)h(0) y(1)=x(0)h(1) +x(1)h(0) 74 Example of Convolution y(0)=x(0)h(0) y(1)=x(0)h(1) h(1 -k)=h[-(k-1)] h(2 -k)=h[-(k-2)] +x(1)h(0) y(1)=x(0)h(1) +x(1)h(0) 74](http://slidetodoc.com/presentation_image_h/02fddd6aecf219a95a72161f2032b845/image-74.jpg)
Example of Convolution y(0)=x(0)h(0) y(1)=x(0)h(1) h(1 -k)=h[-(k-1)] h(2 -k)=h[-(k-2)] +x(1)h(0) y(1)=x(0)h(1) +x(1)h(0) 74
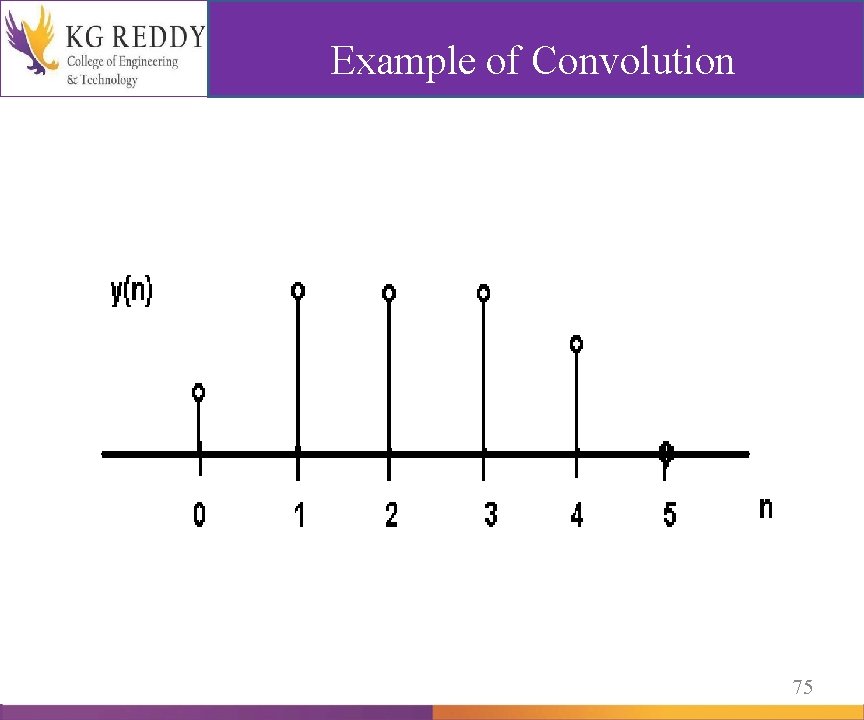
Example of Convolution 75
![Example of Convolution • Convolute two sequences x[n] = {a, b, c} & h[n] Example of Convolution • Convolute two sequences x[n] = {a, b, c} & h[n]](http://slidetodoc.com/presentation_image_h/02fddd6aecf219a95a72161f2032b845/image-76.jpg)
Example of Convolution • Convolute two sequences x[n] = {a, b, c} & h[n] = [e, f, g] Convoluted output = [ ea, eb+fa, ec+fb+ga, fc+gb, gc] 76
![Example of Convolution Example: Convolute two sequences x[n] = {1, 2, 3} & h[n] Example of Convolution Example: Convolute two sequences x[n] = {1, 2, 3} & h[n]](http://slidetodoc.com/presentation_image_h/02fddd6aecf219a95a72161f2032b845/image-77.jpg)
Example of Convolution Example: Convolute two sequences x[n] = {1, 2, 3} & h[n] = {-1, 2, 2} Convoluted output y[n] = [ -1, -2+2, -3+4+2, 6+4, 6] = [-1, 0, 3, 10, 6] 77

Convolution Integral 78

Operation of convolution 79
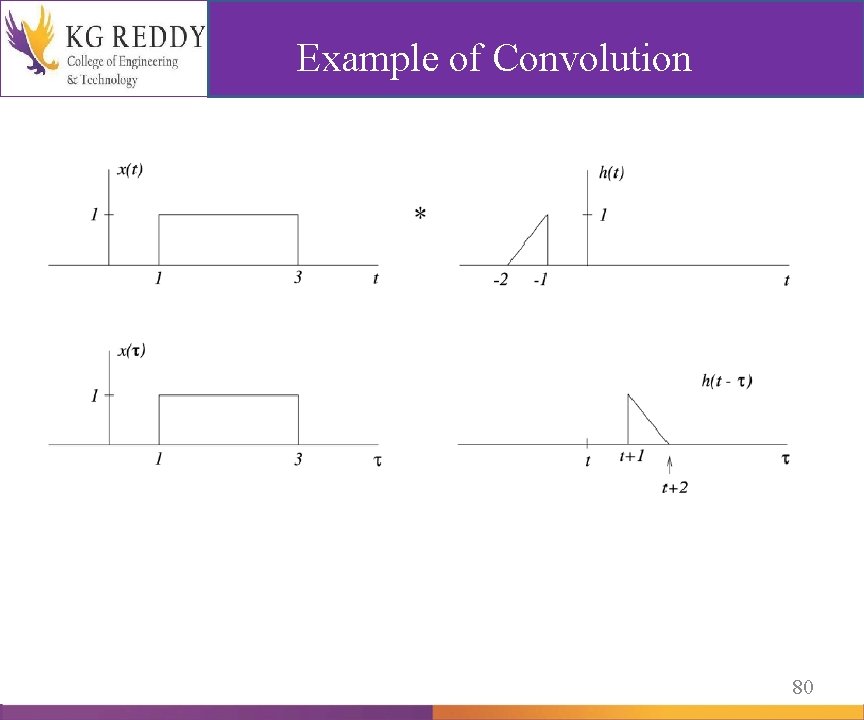
Example of Convolution 80
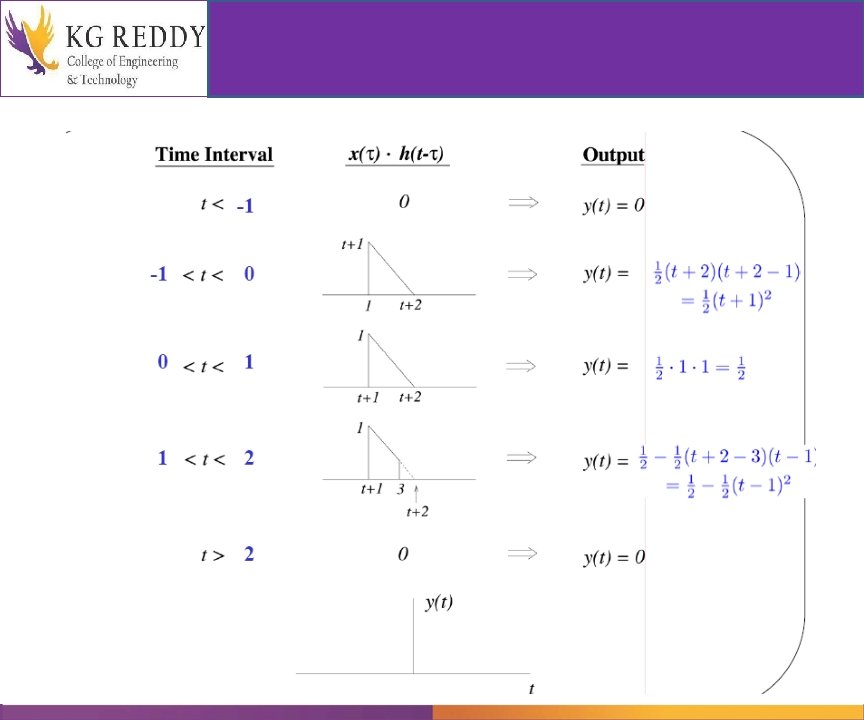
81

82

83

Presented by M. N. Narsaiah Head – IQAC Associate Professor, ECE Department 1

Laplace Transform Introduction: Laplace Transform is used to convert the time domain signal to complex frequency domain (also known as Laplace domain or S-domain) signal. This transformation was first proposed by Laplace in the year 1780. Later adapted for various engineering applications for Quality Audit in Academics solving differential equations, hence this transformation is Signals and Systems known as Laplace transform. In time domain equations governing a system will be in the form of differential equation, while transforming the system to s-domain, the differential equations are transformed to simple algebraic equations and the analysis will be much easier in sdomain. 85

Laplace Transform Definition: • The Laplace transform is a linear operator that switched a function f(t) to F(s), Specifically: where: Go from time argument with real input to a complex angular frequency input which is complex 86

Restrictions There are two governing factors that determine whether Laplace transforms can be used: • f(t) must be at least piecewise continuous for t ≥ 0 • |f(t)| ≤ Meγ t where M and γ are constants Boundedness: This criterion also follows directly from the general definition: If f(t) is not bounded by Meγt then the integral will not converge 87

Region of Convergence(ROC) If x(t) � X(s) where X(s) = The set of values ‘s’ for which the on of Convergence(ROC) integral converges is known as Region of Convergence (Ro. C) 88

Laplace Transform General Theory Example Convergence 89

Laplace Transforms x(t) X(s) ROC 90

Laplace Transforms x(t) X(s) ROC 91

Z-Transform Analysis of discrete time LTI systems can be done using ztransforms. It is a powerful mathematical tool The bilateral two sided z-transform of a discrete time signal x (n) is given as The unilateral one sided z-transform of a discrete time signal x(n) is given as 92

Z-Transform of a discrete time signal x(n) can be represented with X(z) and it is defined as the 93

Inverse Z-transform 94

Z-Plane Im z = e j Re Fourier Transform is to evaluate z-transform on a unit circle. 95

Region of Convergence(ROC) Give a sequence, the set of values of z for which the z-transform converges, i. e. , |X(z)|< , is called the region of convergence. ROC is centered on origin and consists of a set of rings. 96

Example: Region of Convergence Im ROC is an angual ring centered on the origin. ROC is an annual ring centered on the origin. r Re 97

Stable Systems A stable system requires that its Fourier transform is uniformly convergent. Fact: Fourier transform is to evaluate z-transform on a unit circle. A stable system requires the ROC of z-transform to include the unit circle. 98

Represent z-transform as a Rational Function where P(z) and Q(z) are polynomials in z. Zeros: The values of z’ s such that X(z) = 0 Poles: The values of z’ s such that X(z) = 99
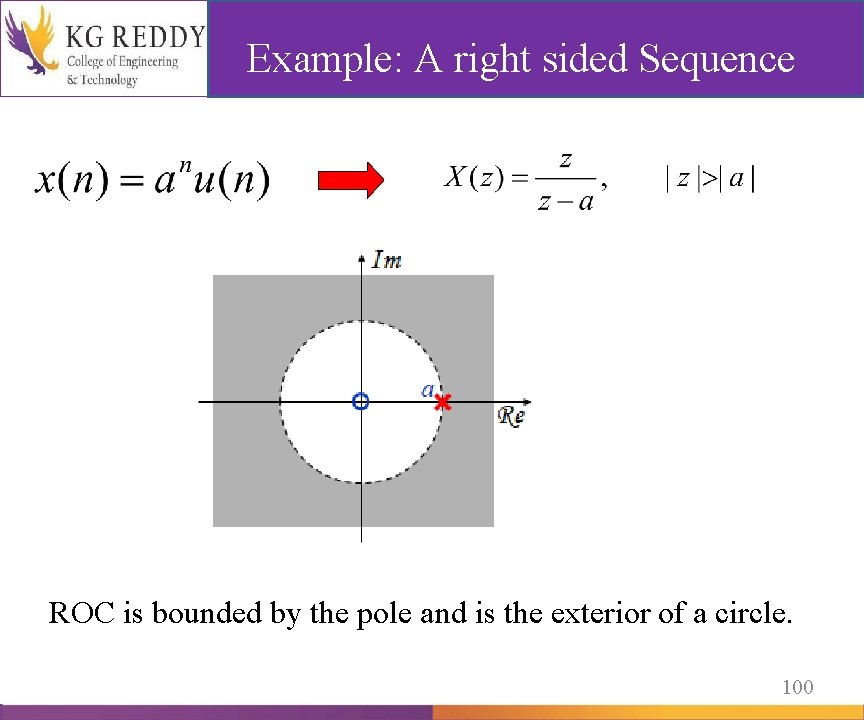
Example: A right sided Sequence ROC is bounded by the pole and is the exterior of a circle. 100
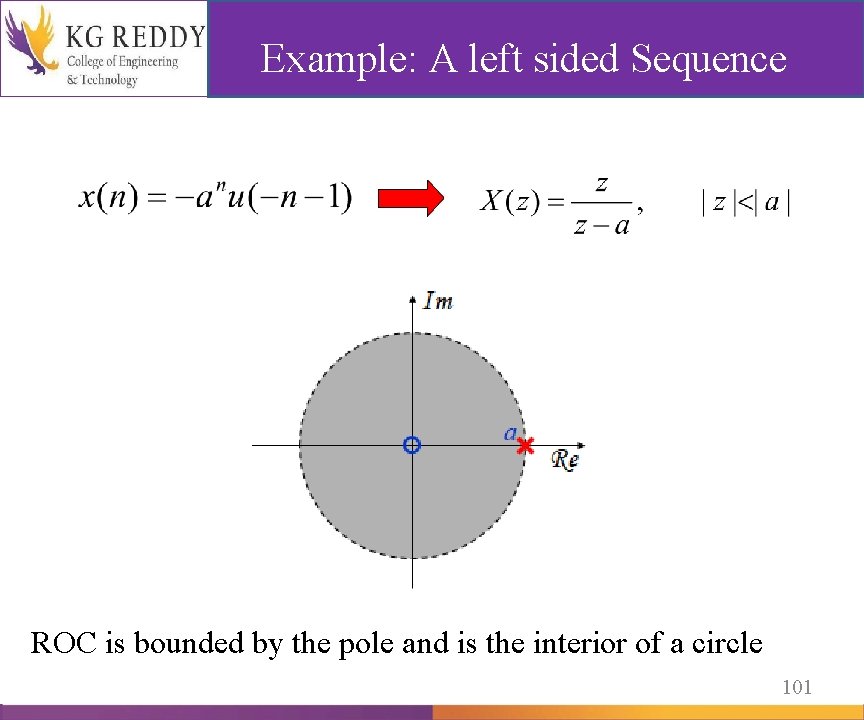
Example: A left sided Sequence ROC is bounded by the pole and is the interior of a circle 101
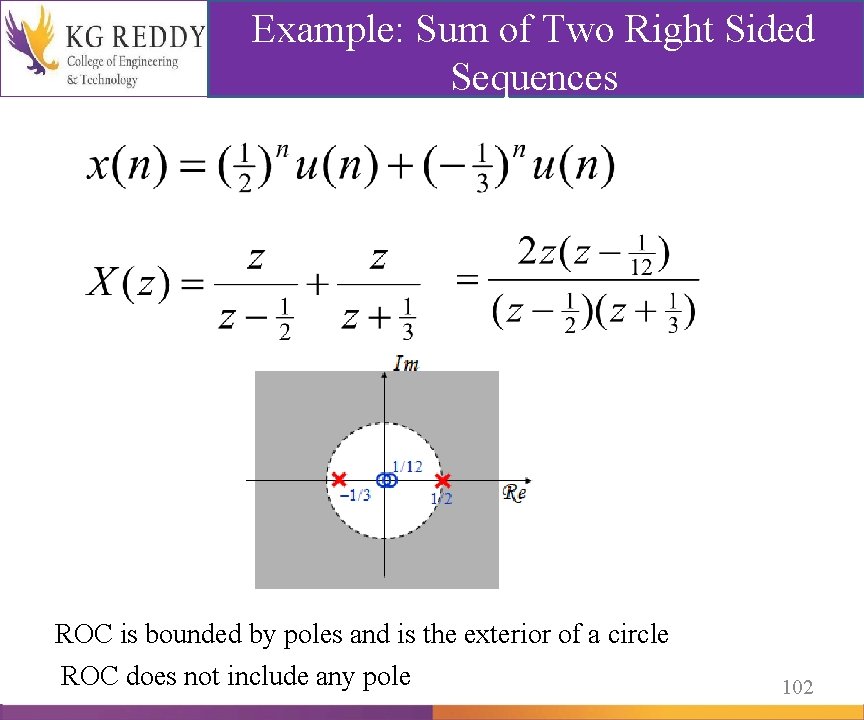
Example: Sum of Two Right Sided Sequences ROC is bounded by poles and is the exterior of a circle ROC does not include any pole 102

Example: A Two Sided Sequence Im ROC is bounded by poles and is a ring. 1/12 1/3 1/2 Re ROC does not include any pole.
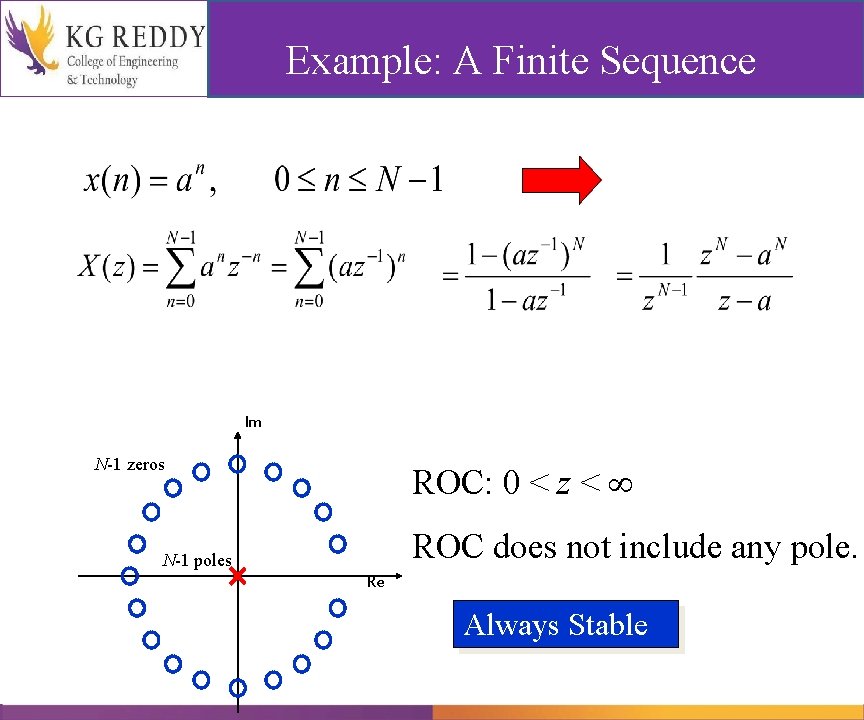
Example: A Finite Sequence Im N-1 zeros ROC: 0 < z < ROC does not include any pole. N-1 poles Re Always Stable

Properties of ROC • A ring or disk in the z-plane centered at the origin. • The Fourier Transform of x(n) is converge absolutely if the ROC includes the unit circle. • The ROC cannot include any poles • Finite Duration Sequences: The ROC is the entire z-plane except possibly z = 0 or z = . • Right sided sequences: The ROC extends outward from the outermost finite pole in X(z) to z = . • Left sided sequences: The ROC extends inward from the innermost nonzero pole in X(z) to z = 0.

Z-Transform Pairs Sequence z-Transform ROC All z except 0 (if m>0) or (if m<0)

Z-Transform Pairs Sequence z-Transform ROC

Presented by M. N. Narsaiah Head – IQAC Associate Professor, ECE Department 1
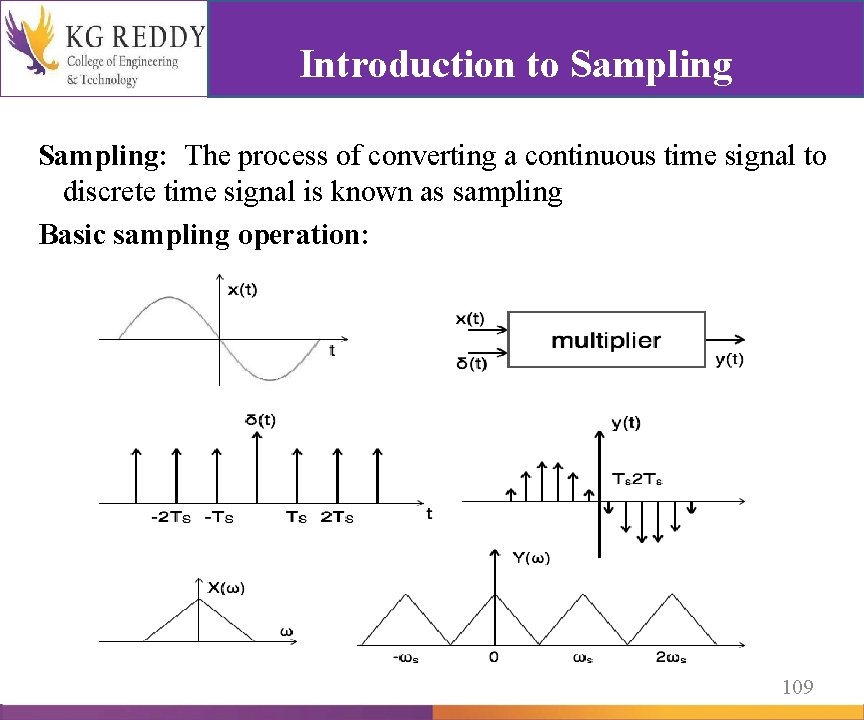
Introduction to Sampling: The process of converting a continuous time signal to discrete time signal is known as sampling Basic sampling operation: 109

Sampling theorem Statement: Any continuous time signal is band limited to fm Hz can be reconstructed from its samples if the sampling rate(1/ Ts) or sampling frequency (fs ) is ≥ 2 fm fs ≥ 2 fm where Ts is sampling time period or sampling interval Signals and Systems Quality Audit in Academics fs is sampling frequency fs = 1/ Ts fm is the highest frequency of the signal if the signal consist of multiple frequencies 110
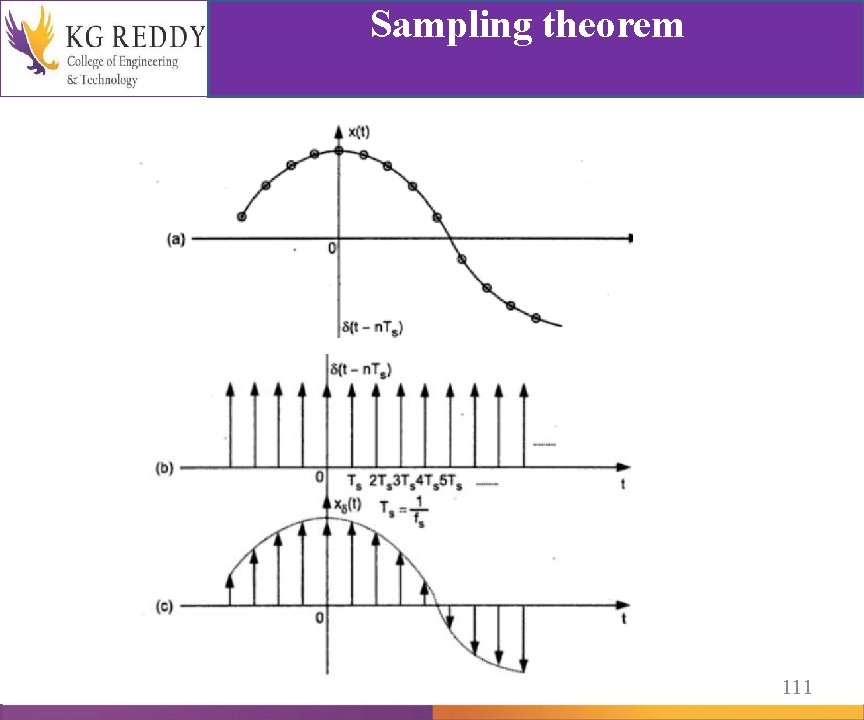
Sampling theorem 111

Sampling theorem 112

Spectrum of sampled signal 113
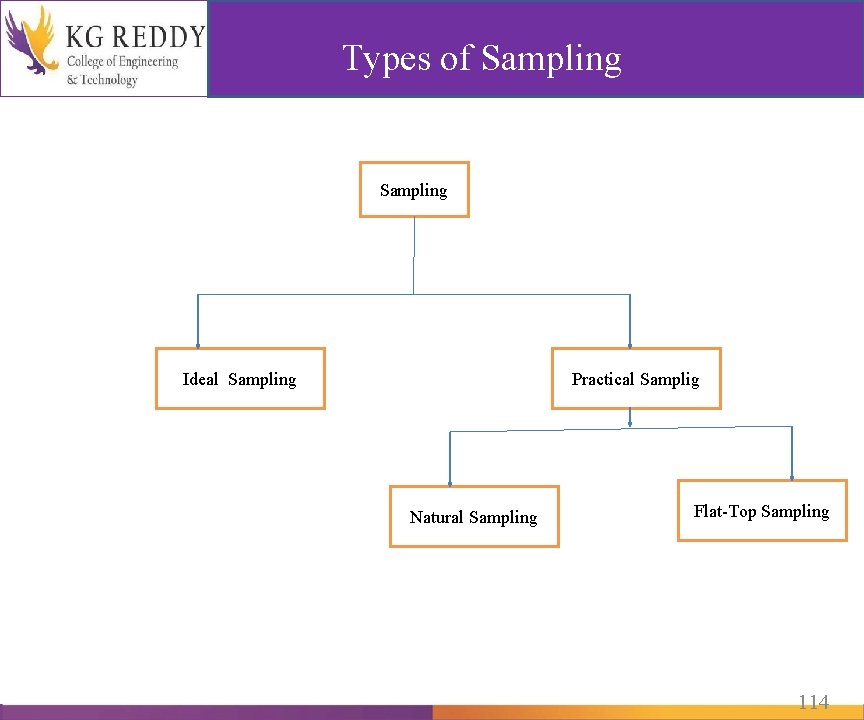
Types of Sampling Ideal Sampling Practical Samplig Natural Sampling Flat-Top Sampling 114

Sampling of Band pass sampling Band pass signal is sampled by the following sampling rate fs ≥ 2 fh / N where N= int (fh /(fh- fl)) fs is sampling frequency fh is the highest frequency of the signal fl is the lowest frequency of the signal fs = 1/ Ts Ts is sampling time period or sampling interval 115

Correlation of signals Correlation is used to measure the similarity between two signals ∞ R(τ) = ∫ x 1 (t) x 2 (t − τ) dt −∞ Types of Correlation: 1. Auto correlation 2. Cross correlation Auto correlation: Auto correlation is used to measure the similarity between a signal x(t) and delayed x(t- t 0) or advanced version x(t + t 0) of it. Cross correlation: Cross correlation is used to measure the similarity between two different signals x 1 (t) and x 2(t) 116

Auto correlation of non-periodic signals Consider two non-periodic or energy signals x 1 (t) and x 2 (t) the cross correlation function of these two signals is given by, ∞ R 11(τ) = R(τ) = ∫ x 1(t)x(t − τ) dt [+ve shift] −∞ = ∫ x(t) x(t + τ) dt [-ve shift] −∞ Where τ = searching or scanning or delay parameter. If the signal is complex then auto correlation function is given by R 11 (τ) = R(τ) = ∫ x(t) x ∗ (t − τ) dt = ∫ x(t + τ) x ∗ (t) dt 117

Auto correlation of non periodic signals Consider two non-periodic or energy signals x 1 (t) and x 2 (t) the cross correlation function of these two signals is given by, ∞ R 12(τ) = R(τ) = ∫ x 1(t) x 2(t − τ) dt [+ve shift] −∞ = ∫ x 1(t+ τ) x 2(t ) dt [-ve shift]7 −∞ Where τ = searching or scanning or delay parameter. If the signal is complex then auto correlation function is given by ∞ R 12 (τ) = R(τ) = ∫ x 1(t) x 2 ∗ (t − τ) dt [+ve shift] −∞ = ∫ x 1(t + τ) x 2 ∗ (t) dt [-ve shift] −∞ 118

Auto correlation of non-periodic signals Consider two non-periodic or energy signals x 1 (t) and x 2 (t) the cross correlation function of these two signals is given by, ∞ R 12(τ) = R(τ) = ∫ x 1(t)x 2(t − τ) dt [+ve shift] −∞ = ∫ x 1(t) x 2(t + τ) dt [-ve shift] −∞ Where τ = searching or scanning or delay parameter. If the signal is complex then auto correlation function is given by R 12 (τ) = R(τ) = ∫ x 1(t) x 2 ∗ (t − τ) dt = ∫ x 2(t + τ) x 1 ∗ (t) dt 119

Properties of auto correlation (periodic signal) 120

Cross correlation c signal C 121

Cross correlation of non-periodic signal • Cross correlation of non-periodic signal is given by 122

Properties of cross correlation (non- periodic signal) 123

Cross correlation of periodic signal 124
- Slides: 124