Signals and Systems Ch 1 Introduction What is

信号与系统 Signals and Systems

Ch 1 Introduction (绪论) 本章重点: • What is a signal? 什么是信号? • What is a system? 什么是系统? • Classifications of signals 信号的分类 • Basic operations of signals 信号的基本运算 • Basic signals 基本信号 • Properties of systems 系统的特性

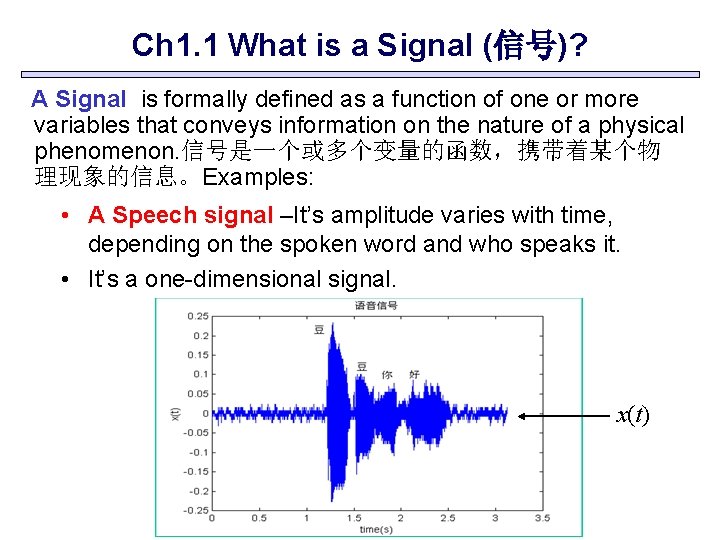
Ch 1. 1 What is a Signal (信号)? A Signal is formally defined as a function of one or more variables that conveys information on the nature of a physical phenomenon. 信号是一个或多个变量的函数，携带着某个物 理现象的信息。Examples: • A Speech signal –It’s amplitude varies with time, depending on the spoken word and who speaks it. • It’s a one-dimensional signal. x(t)

What is a Signal? • An image is a function of two spatial coordinates. • It’s a two-dimensional signal. I(x, y)

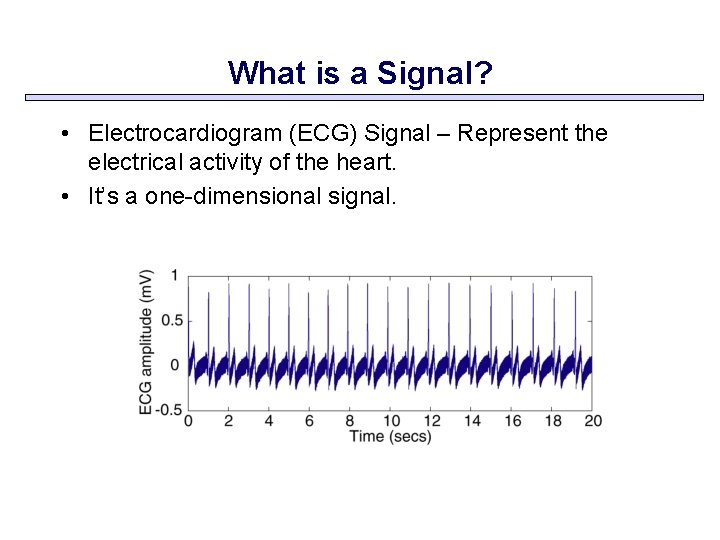
What is a Signal? • Electrocardiogram (ECG) Signal – Represent the electrical activity of the heart. • It’s a one-dimensional signal.

Ch 1. 2 What is a System(系统)? A System is formally defined as an entity that manipulates one or more signals to accomplish a function, thereby yielding new signals.

Ch 1. 3 Overview of Specific Systems Examples: Communication Systems(通信系统) Elements of a communication system. The transmitter changes the message signal into a form suitable for transmission over the channel. The receiver processes the channel output (i. e. , the received signal) to produce an estimate of the message signal.

(a) Snapshot of Pathfinder exploring the surface of Mars. The 70 -meter (230 foot) diameter antenna located at Canberra, Australia. The surface of the 70 -meter reflector must remain accurate within a fraction of the signal’s wavelength. (Courtesy of Jet Propulsion Laboratory. )

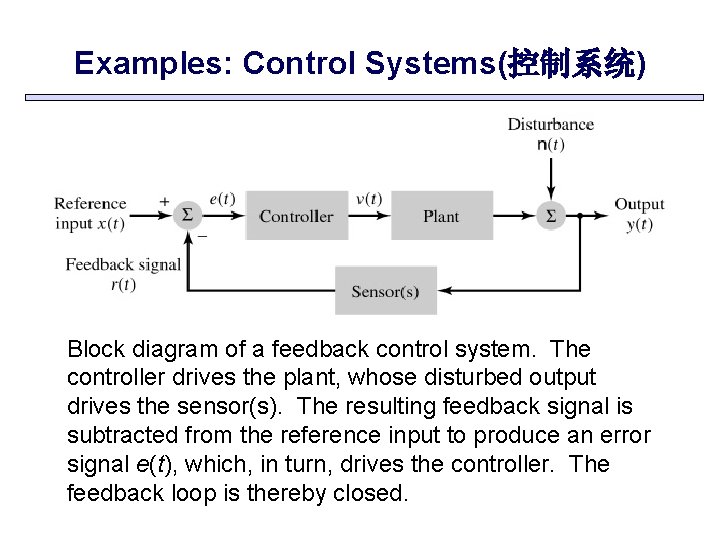
Examples: Control Systems(控制系统) Block diagram of a feedback control system. The controller drives the plant, whose disturbed output drives the sensor(s). The resulting feedback signal is subtracted from the reference input to produce an error signal e(t), which, in turn, drives the controller. The feedback loop is thereby closed.

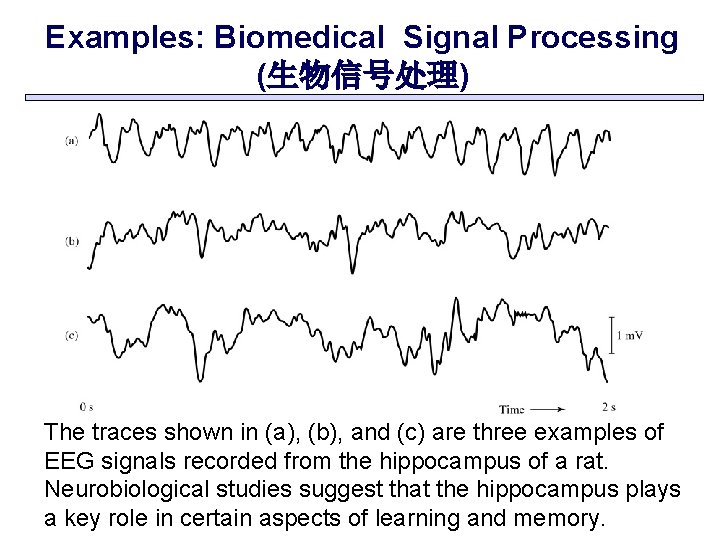
Examples: Biomedical Signal Processing (生物信号处理) The traces shown in (a), (b), and (c) are three examples of EEG signals recorded from the hippocampus of a rat. Neurobiological studies suggest that the hippocampus plays a key role in certain aspects of learning and memory.

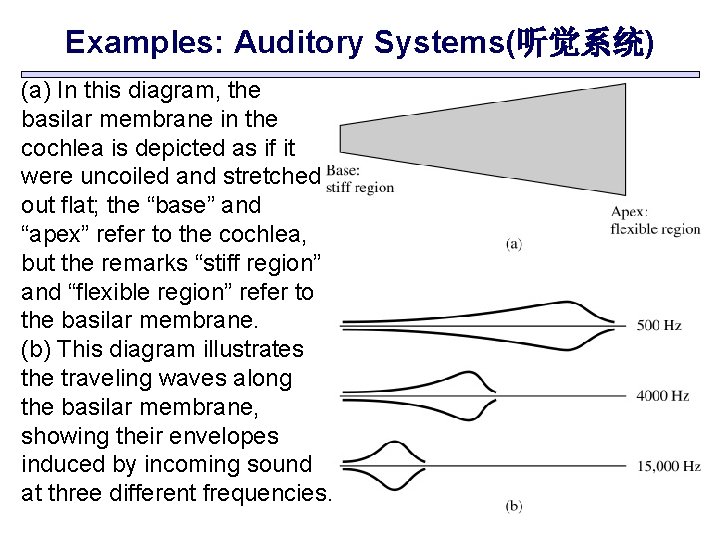
Examples: Auditory Systems(听觉系统) (a) In this diagram, the basilar membrane in the cochlea is depicted as if it were uncoiled and stretched out flat; the “base” and “apex” refer to the cochlea, but the remarks “stiff region” and “flexible region” refer to the basilar membrane. (b) This diagram illustrates the traveling waves along the basilar membrane, showing their envelopes induced by incoming sound at three different frequencies.

主要参考书 [1] Simon H. , Barry V. V. Signals and Systems. John Wiley & Sons, Inc. 1999 [2] Edward W. K. , Bonnie S. H. Fundamentals of Signals and Systems Using MATLAB. Prentice-Hall International, Inc. 1997 [3] A. V. Oppenheim. Signals and Systems 或中译本（第 2版）. 西安交通大学出版社. [4] 郑君里，应启珩等. 信号与系统. 第 2版. 高等教育出版社，2000.

Ch 1. 4 classifications of signals (信号的分类) 1. continuous-time and discrete-time signals 连续时间信号和离散时间信号 2. periodic and non-periodic signals 周期信号和非周期信号 3. deterministic and random signals 确定信号和随机信号 4. Energy and power signals 能量信号和功率信号

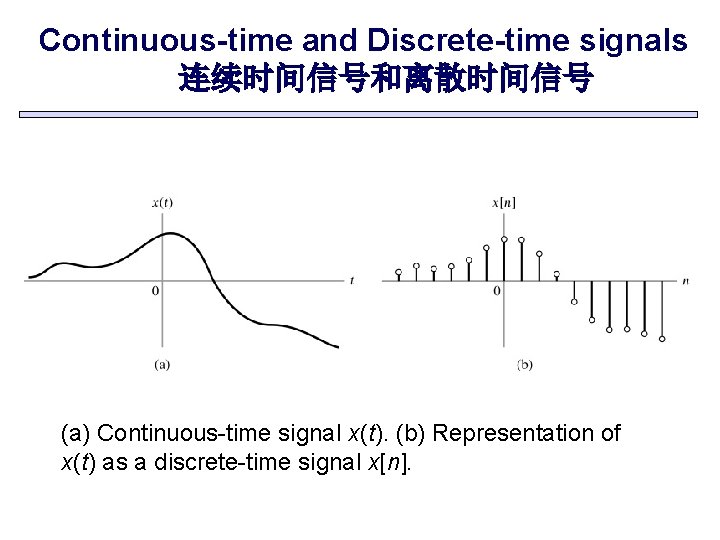
Continuous-time and Discrete-time signals 连续时间信号和离散时间信号 (a) Continuous-time signal x(t). (b) Representation of x(t) as a discrete-time signal x[n].

Continuous-time and Discrete-time signals 连续时间信号和离散时间信号 • Continuous-time signal: a signal if it is defined for all time t. 连续时间信号：若信号在所有时间t 处都有定义, 用x(t)表示。 • Discrete-time signal : a signal if it is defined only at discrete instants of time. 离散时间信号：若信号仅在某些离散时刻处有定义, 用x[n]表示。 • 离散信号可以由连续信号取样(sampling)得来： x[n]=x(t)|t=n. T =x(n. T) T：取样间隔

periodic and non-periodic signals 周期信号和非周期信号 (a) Square wave with amplitude A = 1 and period T = 0. 2 s. (b) Rectangular pulse of amplitude A and duration T 1.

periodic and nonperiodic signals 周期信号和非周期信号 Periodic signals are such that x(t+T) = x(t) for all t. The smallest value of T that satisfies the definition is called the period(周期). In general, for CT signals for DT signals Where r, N are integers

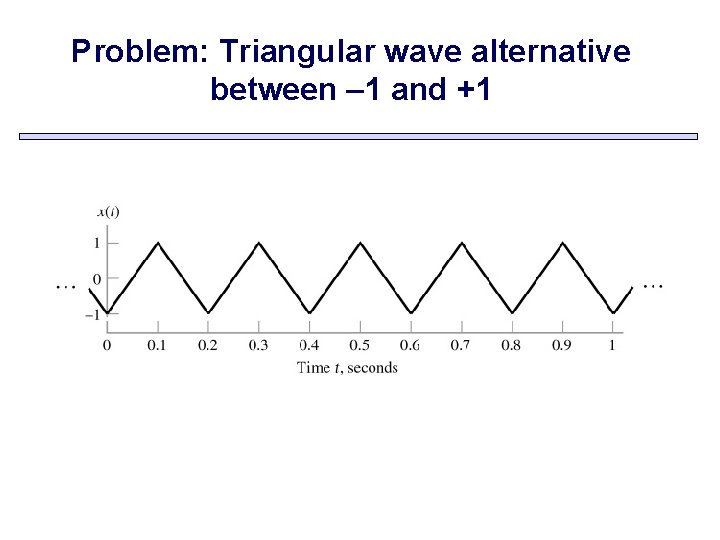
Problem: Triangular wave alternative between – 1 and +1

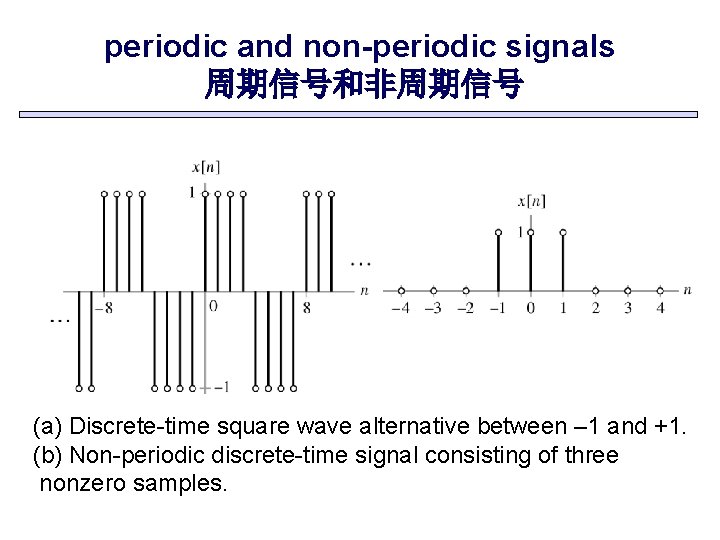
periodic and non-periodic signals 周期信号和非周期信号 (a) Discrete-time square wave alternative between – 1 and +1. (b) Non-periodic discrete-time signal consisting of three nonzero samples.

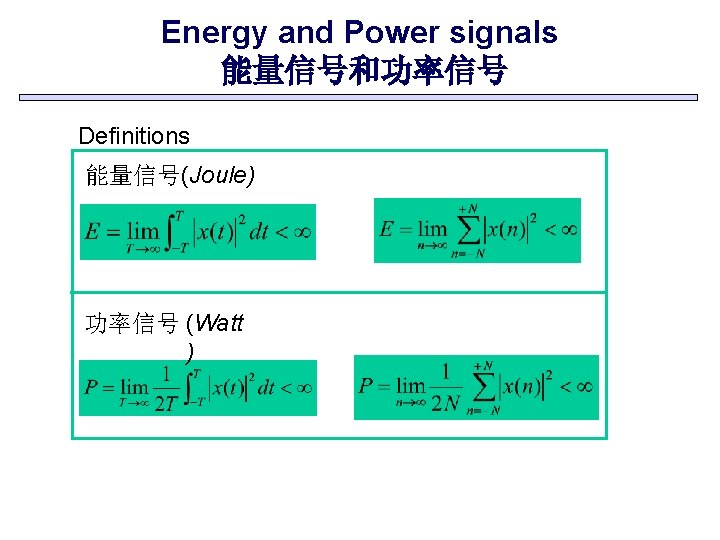
Energy and Power signals 能量信号和功率信号 Definitions 能量信号(Joule) 功率信号 (Watt )

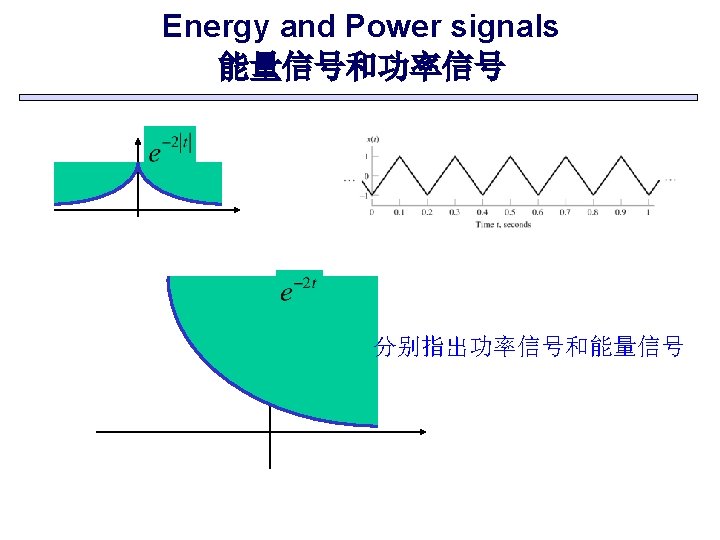
Energy and Power signals 能量信号和功率信号 Problem: Determine the average power of the triangular wave.

Energy and Power signals 能量信号和功率信号 Problem: Determine the total energy of the discrete-time signal.

Deterministic and Random Signals 确定性信号和随机信号 x[n] … … 0 N n

Deterministic and Random Signals 确定性信号和随机信号 X(t) t t t

operations performed on dependent variables (基于从变量的运算) 1. Amplitude scaling (幅度比例变化) x(t) cx(t) x[n] cx[n] (c为常数) 波形不变，幅度成比例放大或缩小。 Example：x(t)=sin(2π× 10 t) ; y(t)=5 x(t)=5 sin(2π× 10 t) ;

operations performed on dependent variables (基于从变量的运算) 2. Addition (信号相加) y(t) = x 1(t)+x 2(t) y(n) = x 1[n]+x 2[n] 3. Multiplication (信号相乘) y(t) = x 1(t) x 2(t) y(n) = x 1[n] x 2[n]

operations performed on dependent variables (基于从变量的运算) 4. Differentiation(连续信号的微分) 5. integration（连续信号的积分）

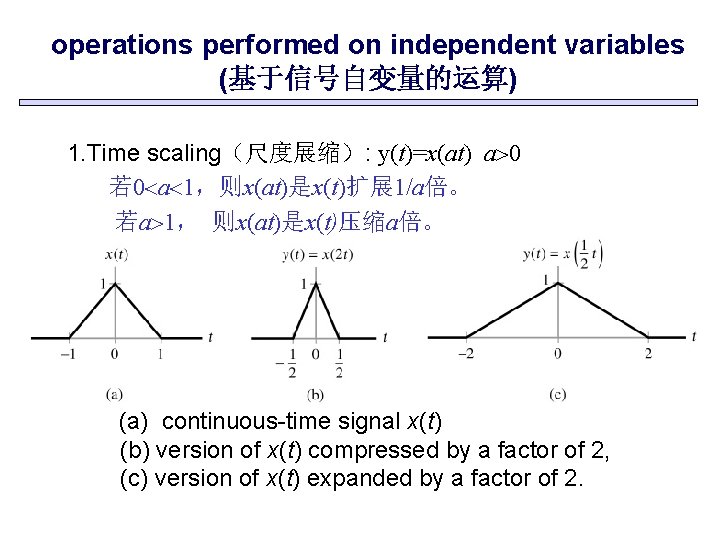
operations performed on independent variables (基于信号自变量的运算) 1. Time scaling（尺度展缩）: y(t)=x(at) a>0 若 0<a<1，则x(at)是x(t)扩展 1/a倍。 若a>1， 则x(at)是x(t)压缩a倍。 (a) continuous-time signal x(t) (b) version of x(t) compressed by a factor of 2, (c) version of x(t) expanded by a factor of 2.

Time scaling（尺度展缩） y[n]= x[kn] (a) discrete-time signal x[n] (b) version of x[n] compressed by a factor of 2, with some values of the original x[n] lost as a result of the compression.

operations performed on independent variables (基于信号自变量的运算) 2. reflection（ 翻转）: y(t)=x(-t)表示将x(t)以纵轴为中心作 180 翻转。 (a) continuous-time signal x(t) (b) reflected version of x(t) about the origin.

Reflection（ 翻转） 2. reflection（ 翻转）: x[n] x[-n] x[n]以纵轴为中心作 180 翻转 Problem: Find the reflected version of x[n] and y[n]

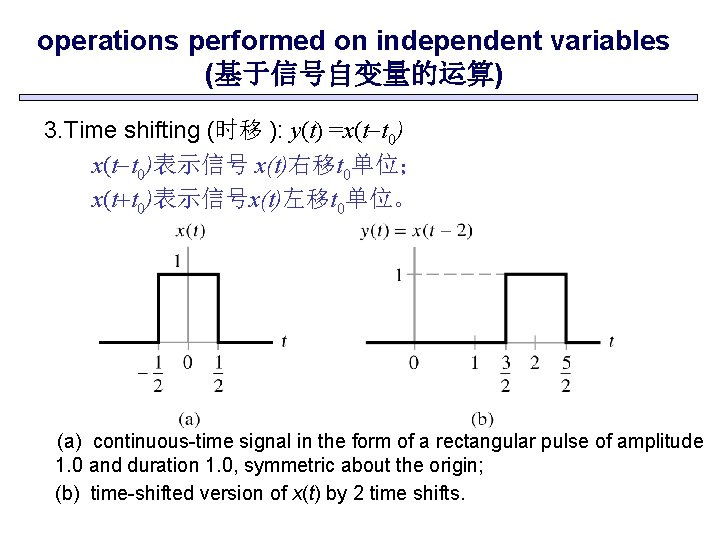
operations performed on independent variables (基于信号自变量的运算) 3. Time shifting (时移 ): y(t) =x(t-t 0)表示信号 x(t)右移t 0单位； x(t+t 0)表示信号x(t)左移t 0单位。 (a) continuous-time signal in the form of a rectangular pulse of amplitude 1. 0 and duration 1. 0, symmetric about the origin; (b) time-shifted version of x(t) by 2 time shifts.

Time shifting (时移 ) y[n]=x[n k] ，k>0 x[n+k]，左移k单位； x[n-k]， 右移k单位。 Problem: Find the time-shifted signal y[n]= x[n+3]

operations performed on independent variables (基于信号自变量的运算) 总结公式：

operations performed on independent variables (基于信号自变量的运算) Example: 已知x(t)的波形如图所示，试画出x(2 t)、 x(t/3)、 x(t+6) 、x(-t)、 x(6 -2 t)的波形。

operations performed on independent variables ( 基于信号自变量的运算) Example: 已知x(n)的波形如图所示，求x[n+2]、 x[-n] 、 x[-n-2]、x[-n/3]、 x[2 n] 的波形。

Ch 1. 6 Basic Signals 基本信号 1. Exponential Signals 指数信号 2. Sinusoidal Signals 正弦信号 3. Exponential Damped Sinusoidal Signals 按指数 衰减的正弦信号 4. Step Signals 阶跃信号 5. Impulse Signals 冲激信号 6. Derivatives of The Impulse 冲激信号的导数 7. Ramp Function 斜坡函数

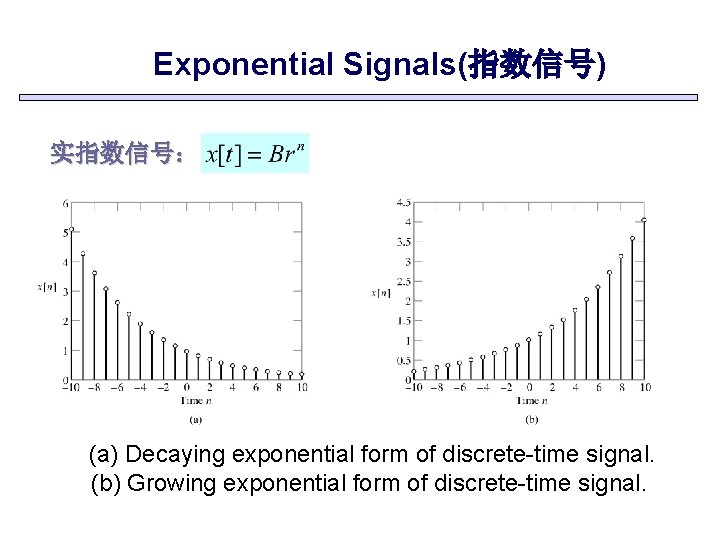
Exponential Signals 指数信号 实指数信号： (a) Decaying exponential form of continuous-time signal. (b) Growing exponential form of continuous-time signal.

Examples of Exponential Signals 指数信号 Lossy capacitor, with the loss represented by shunt resistance R.

Exponential Signals(指数信号) 实指数信号： (a) Decaying exponential form of discrete-time signal. (b) Growing exponential form of discrete-time signal.

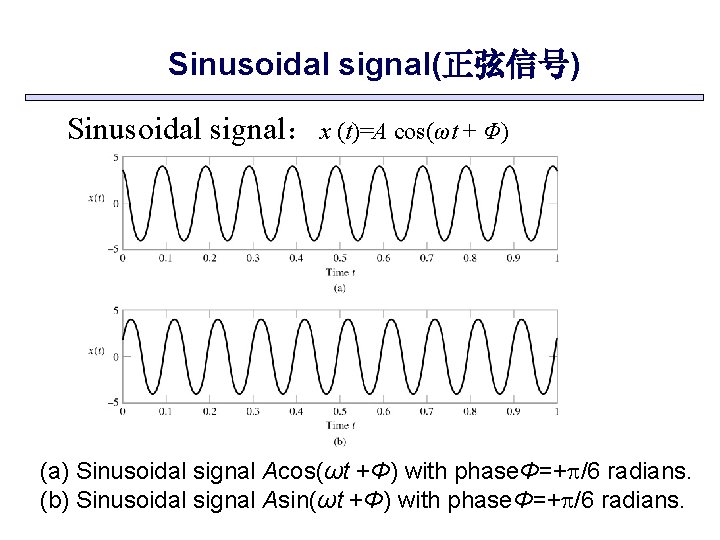
Sinusoidal signal(正弦信号) Sinusoidal signal： x (t)=A cos(ωt + Φ) (a) Sinusoidal signal Acos(ωt +Φ) with phaseΦ=+ /6 radians. (b) Sinusoidal signal Asin(ωt +Φ) with phaseΦ=+ /6 radians.

Examples of Sinusoidal signal 正弦信号 Parallel LC circuit, assuming that the inductor L and capacitor C are both ideal.

Sinusoidal signal 正弦信号 Discrete-time sinusoidal signal.

Relation between Sinusoidal and Complex Exponential Signals 正弦信号和复指数信号的关系 Complex plane, showing eight points uniformly distributed on the unit circle.

Exponentially damped sinusoidal signal 按指数衰减的正弦信号 x (t)= Ae-at sin(ωt)， α >0 Exponentially damped sinusoidal signal Ae-at sin(ωt), with A = 60 and α = 6.

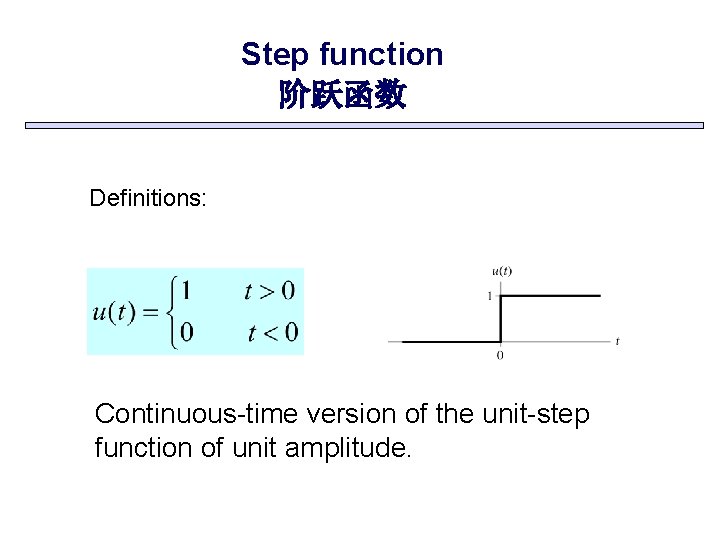
Step function 阶跃函数 Definitions: Continuous-time version of the unit-step function of unit amplitude.

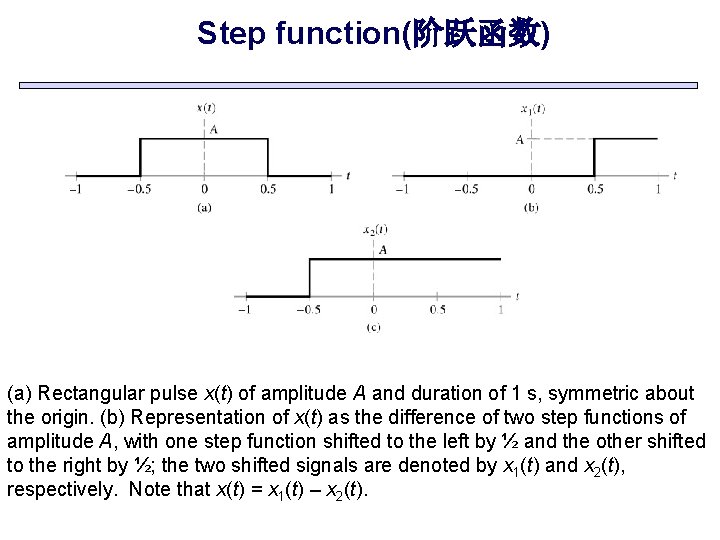
Step function(阶跃函数) (a) Rectangular pulse x(t) of amplitude A and duration of 1 s, symmetric about the origin. (b) Representation of x(t) as the difference of two step functions of amplitude A, with one step function shifted to the left by ½ and the other shifted to the right by ½; the two shifted signals are denoted by x 1(t) and x 2(t), respectively. Note that x(t) = x 1(t) – x 2(t).

Examples of Step function 阶跃函数 (a) Series RC circuit with a switch that is closed at time t = 0, thereby energizing the voltage source. (b) Equivalent circuit, using a step function to replace the action of the switch.

Unit Impulse 单位冲激信号 Definitions: (t)=0 , t 0

Examples of Unit Impulse 冲激信号 (a) Evolution of a rectangular pulse of unit area into an impulse of unit strength (i. e. , unit impulse). (b) Graphical symbol for unit impulse. (c) Representation of an impulse of strength a that results from allowing the duration Δ of a rectangular pulse of area a to approach zero.

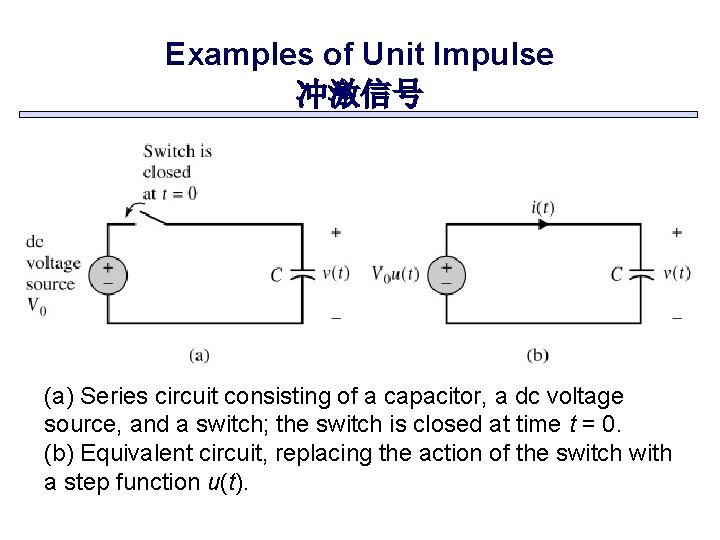
Examples of Unit Impulse 冲激信号 (a) Series circuit consisting of a capacitor, a dc voltage source, and a switch; the switch is closed at time t = 0. (b) Equivalent circuit, replacing the action of the switch with a step function u(t).

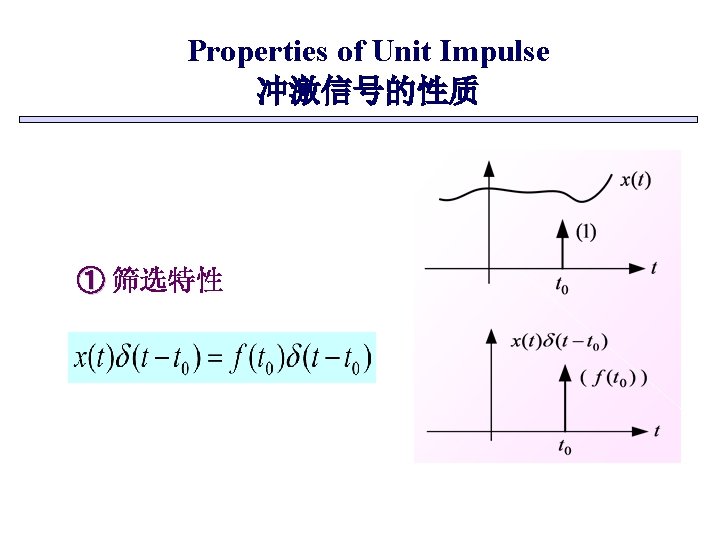
Properties of Unit Impulse 冲激信号的性质 ① 筛选特性

The Time-scaling Property of Unit Impulse 冲激信号的时间展缩 Steps involved in proving the time-scaling property of the unit impulse. (a) Rectangular pulse xΔ(t) of amplitude 1/Δ and duration Δ, symmetric about the origin. (b) Pulse xΔ(t) compressed by factor a. (c) Amplitude scaling of the compressed pulse, restoring it to unit area.

Problems

solution

Derivatives of The Impulse function 冲激函数的导数（冲激偶） Definitions:

Derivatives of The Impulse function 冲激函数的导数（冲激偶） Properties: (筛选特性) (取样特性) (展缩特性)

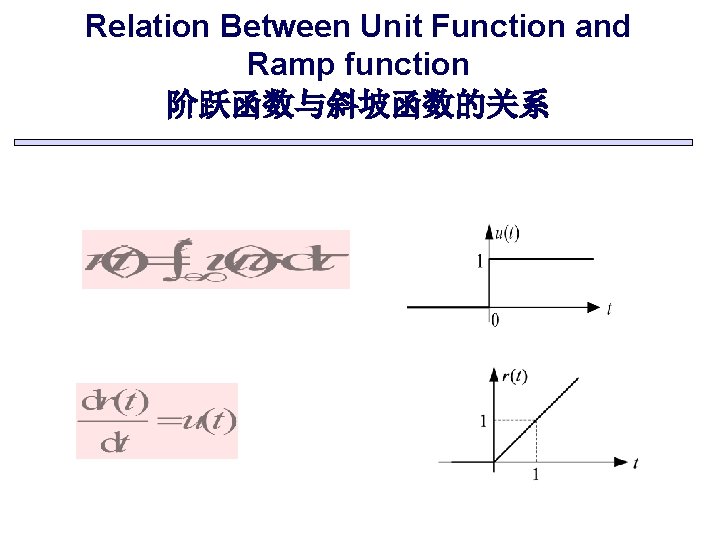
Ramp function(斜坡函数) Definitions:

Relation Between Unit Function and Ramp function 阶跃函数与斜坡函数的关系

Problems (1) 解： (1) (2)

Relations of Impulse Function, Unit Function and Ramp function 冲激函数、阶跃函数与斜坡函数的关系

Ch 1. 7 Systems Viewed as Interconnections of Operations Block diagram representation of operator H for (a) continuous time and (b) discrete time.

Ex: Moving-Average Systems 滑动平均系统：y(n)=[x(n)+x(n-1)+x(n-2)]/3 Discrete-time-shift operator Sk, operating on the discrete-time signal x[n] to produce x[n – k].

Ex: Moving-Average Systems 滑动平均系统：y(n)=[x(n)+x(n-1)+x(n-2)]/3 Two different (but equivalent) implementations of the moving-average system: (a) cascade form of implementation and (b) parallel form of implementation.

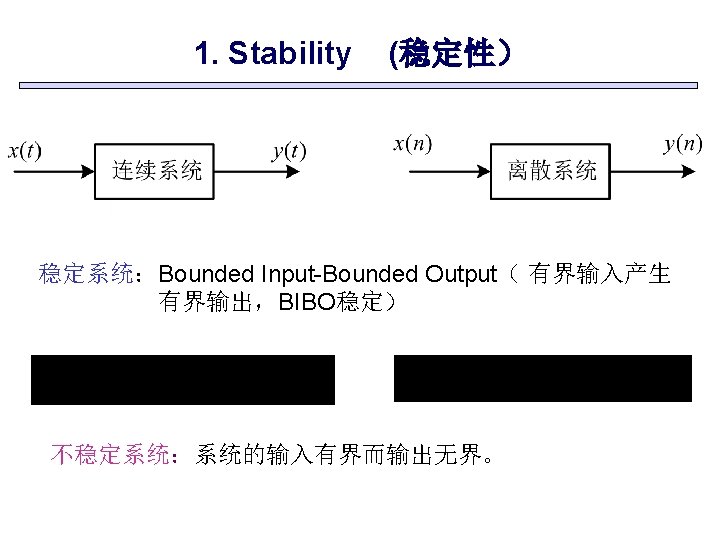
Ch 1. 8 Properties of Systems 1. Stability (稳定性） 2. Causality （因果性） 3. Invertibility （可逆性） 4. Time-Invariance (时不变性) 5. linearity (线性)

Stability (稳定性） Ex: Moving-Average Systems (滑动平均系统). Show that the System is BIBO stable: y(n)=[x(n)+x(n-1)+x(n-2)]/3. Solution：∣y(n)∣=∣x(n)+x(n-1)+x(n-2)∣/3 ≤（Mx+Mx+Mx）/3=Mx ∣y(n)∣有界，系统稳定。 Ex: Unstable System. y(n)=rnx(n) , r>1 Solution：∣x(n)∣≤Mx<∞ ∣y(n)∣=∣rn∣ • ∣x(n)∣, 由于 r>1，∣rn∣→∞，∣y(n)∣无界，系统不稳定

An Unstable System Dramatic photographs showing the collapse of the Tacoma Narrows suspension bridge on November 7, 1940. (a) Photograph showing the twisting motion of the bridge’s center span just before failure. (b) A few minutes after the first piece of concrete fell, this second photograph shows a 600 -ft section of the bridge breaking out of the suspension span and turning upside down as it crashed in Puget Sound, Washington. Note the car in the top right-hand corner of the photograph.

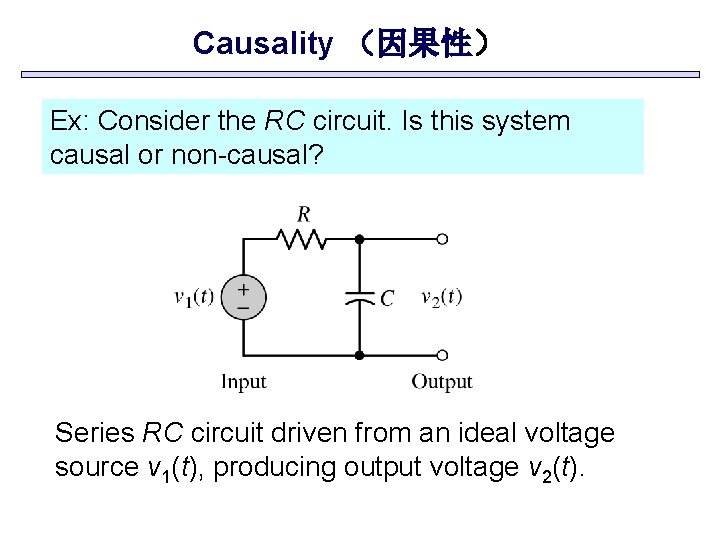
Causality （因果性） Ex: Consider the RC circuit. Is this system causal or non-causal? Series RC circuit driven from an ideal voltage source v 1(t), producing output voltage v 2(t).

3. Invertibility (可逆性) The notion of system invertibility. The second operator Hinv is the inverse of the first operator H. Hence, the input x(t) is passed through the cascade correction of H and H-1 completely unchanged.

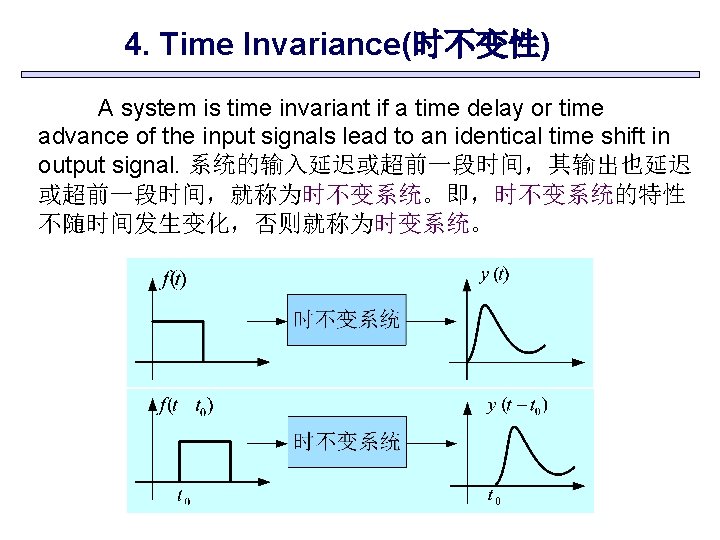
4. Time Invariance(时不变性) The notion of time invariance. (a) Time-shift operator St 0 preceding operator H. (b) Time-shift operator St 0 following operator H. These two situations are equivalent, provided that H is time invariant.

4. Time Invariance(时不变性) A system is time invariant if a time delay or time advance of the input signals lead to an identical time shift in output signal. 系统的输入延迟或超前一段时间，其输出也延迟 或超前一段时间，就称为时不变系统。即，时不变系统的特性 不随时间发生变化，否则就称为时变系统。

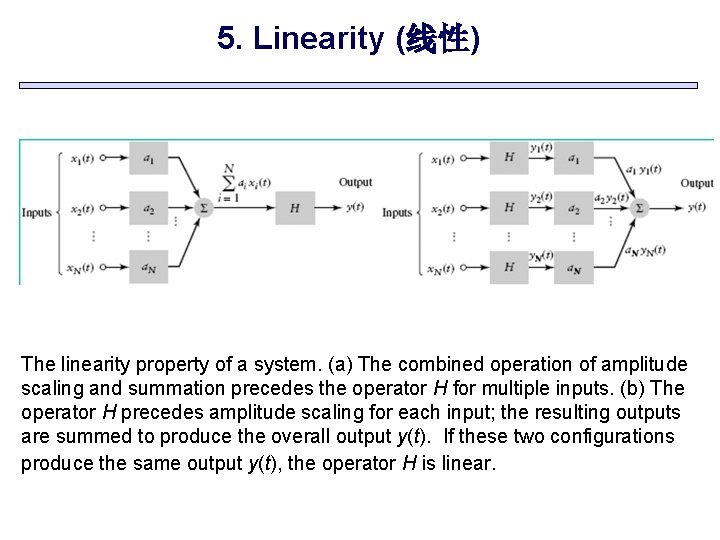
5. Linearity (线性) The linearity property of a system. (a) The combined operation of amplitude scaling and summation precedes the operator H for multiple inputs. (b) The operator H precedes amplitude scaling for each input; the resulting outputs are summed to produce the overall output y(t). If these two configurations produce the same output y(t), the operator H is linear.

Ex: Consider the systems described by the input -output relation. Are the systems linear? 分析: 判断一个系统是否为线性系统，只需判断当 输入激励x(t)变为ax 1(t)+bx 2(t)时，相应的输出响应y(t) 是否也变为 ay 1(t)+by 2(t) y(t-t 0)。

Is the systems linear? solution： The system is nonlinear(非线性系统).

Is the systems linear? solution： The system is linear(线性系统)。

Is the systems linear? solution： The system is linear(线性系统)。 微积分运算是线性运算。