Signals Analysis and Systems ContinuousTime Signal Analysis Outline

Signals Analysis and Systems Continuous-Time Signal Analysis

Outline • Introduction • Fourier Series (FS) representation of Periodic Signals. • Trigonometric and Exponential Form of FS. • Parseval’s Theorem. • Simplifications Through Signal Symmetry. • LTIC System Response to Periodic Inputs.

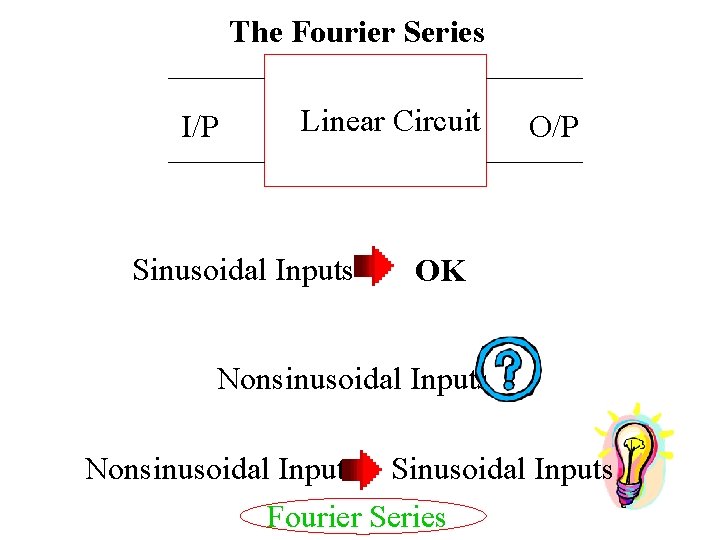
The Fourier Series I/P Linear Circuit Sinusoidal Inputs O/P OK Nonsinusoidal Inputs Sinusoidal Inputs Fourier Series

The Fourier Series Joseph Fourier 1768 to 1830 Fourier (French) studied the mathematical theory of heat conduction. He established the partial differential equation governing heat diffusion and solved it by using infinite series of trigonometric functions.

The Fourier Series Fourier proposed in 1807 A periodic waveform f(t) could be broken down into an infinite series of simple sinusoids which, when added together, would construct the exact form of the original waveform. Consider the periodic function T = Period, the smallest value of T that satisfies the above Equation.

The Fourier Series Definition A Fourier Series is an accurate representation of a periodic signal and consists of the sum of sinusoids at the fundamental and harmonic frequencies. The waveform f(t) depends on the amplitude and phase of every harmonic components, and we can generate any non-sinusoidal waveform by an appropriate combination of sinusoidal functions. http: //archives. math. utk. edu/topics/fourier. Analysis. html

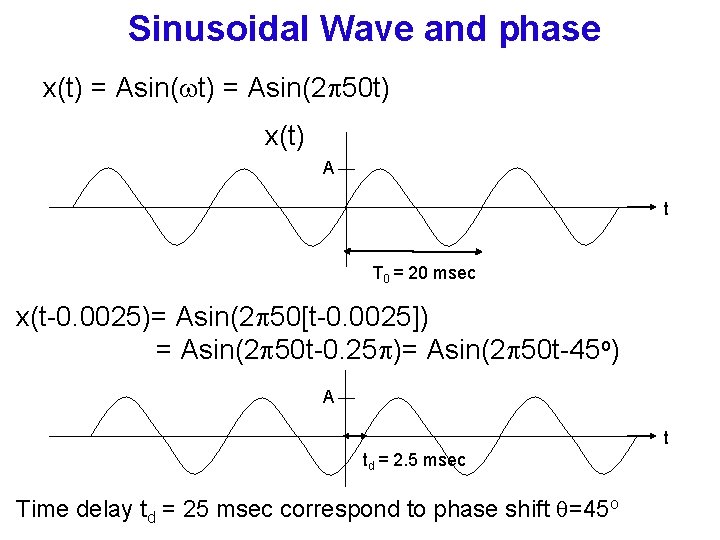
Sinusoidal Wave and phase x(t) = Asin(2 50 t) x(t) A t T 0 = 20 msec x(t-0. 0025)= Asin(2 50[t-0. 0025]) = Asin(2 50 t-0. 25 )= Asin(2 50 t-45 o) A t td = 2. 5 msec Time delay td = 25 msec correspond to phase shift =45 o

Representation of Quantity using Basis • Any number can be represented as a linear sum of the basis number {1, 100, 1000} Ex: 10437 =10(1000) + 4(100) + 3(10) +7(1) • Any 3 -D vector can be represented as a linear sum of the basis vectors {[1 0 0], [0 1 0], [0 0 1]} Ex: [2 4 5]= 2 [1 0 0] + 4[0 1 0]+ 5[0 0 1]

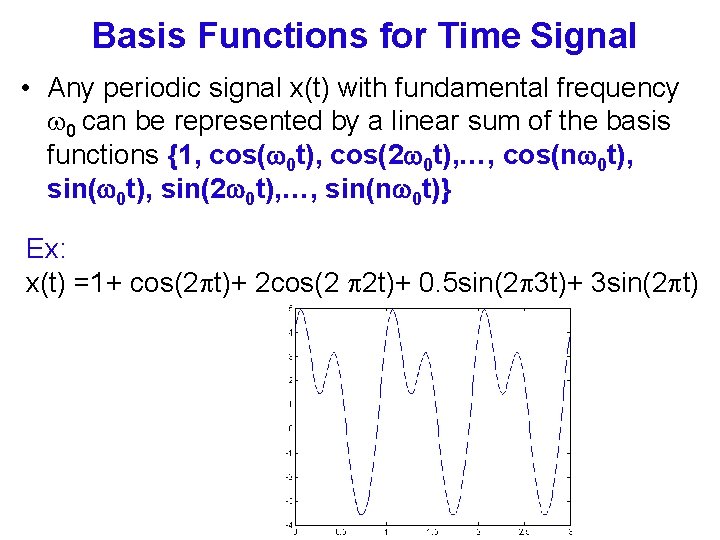
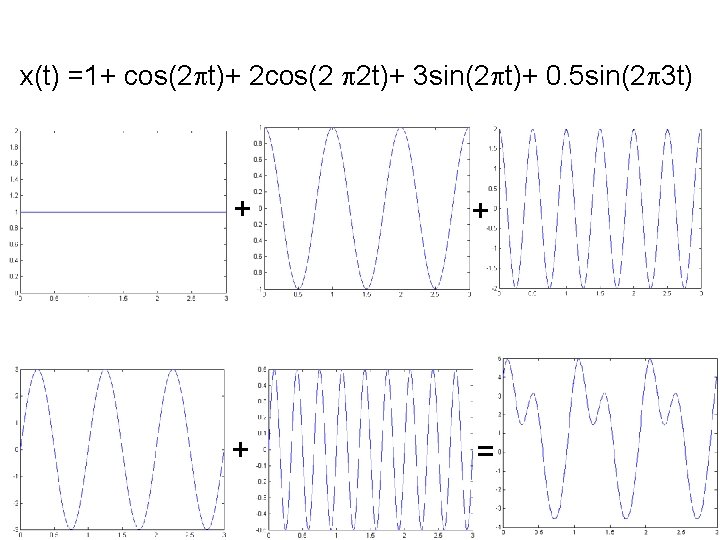
Basis Functions for Time Signal • Any periodic signal x(t) with fundamental frequency 0 can be represented by a linear sum of the basis functions {1, cos( 0 t), cos(2 0 t), …, cos(n 0 t), sin(2 0 t), …, sin(n 0 t)} Ex: x(t) =1+ cos(2 t)+ 2 cos(2 2 t)+ 0. 5 sin(2 3 t)+ 3 sin(2 t)

x(t) =1+ cos(2 t)+ 2 cos(2 2 t)+ 3 sin(2 t)+ 0. 5 sin(2 3 t) + + + =

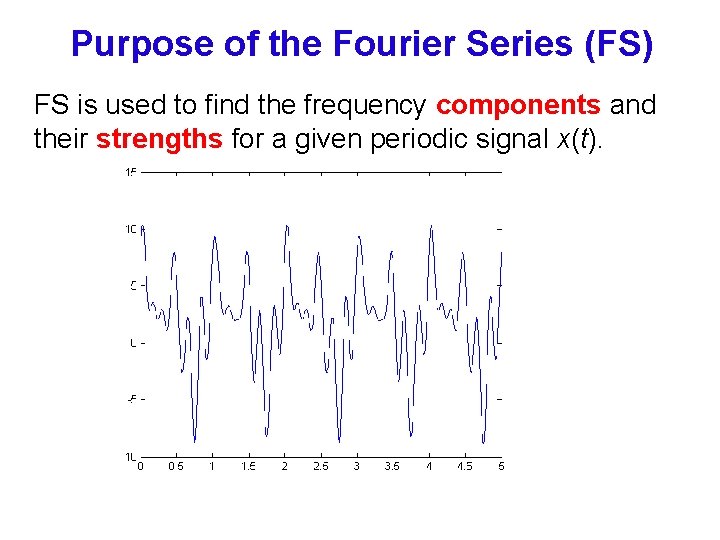
Purpose of the Fourier Series (FS) FS is used to find the frequency components and their strengths for a given periodic signal x(t).

The Three forms of Fourier Series • Trigonometric Form • Compact Trigonometric (Polar) Form. • Complex Exponential Form.

Trigonometric Form • It is simply a linear combination of sines and cosines at multiples of its fundamental frequency, f 0=1/T. • a 0 counts for any dc offset in x(t). • a 0, and bn are called the trigonometric Fourier Series Coefficients. • The nth harmonic frequency is nf 0.

Trigonometric Form • How to evaluate the Fourier Series Coefficients (FSC) of x(t)? To find a 0 integrate both side of the equation over a full period

Trigonometric Form

The Fourier Series To be described by the Fourier Series the waveform f(t) must satisfy the following mathematical properties: 1. f(t) is a single-value function except at possibly a finite number of points. 2. The integral for any t 0. 3. f(t) has a finite number of discontinuities within the period T. 4. f(t) has a finite number of maxima and minima within the period T. In practice, f(t) = v(t) or i(t) so the above 4 conditions are always satisfied.

Example f(t) 1 e-t/2 - 0 • Fundamental period T 0 = p • Fundamental frequency f 0 = 1/T 0 = 1/p Hz w 0 = 2 p/T 0 = 2 rad/s

Compact Trigonometric Form • Usingle sinusoid, • and bn as: are related to the trigonometric coefficients an and

Compact Trigonometric f(t) 1 e-t/2 - 0 • Fundamental period T 0 = p • Fundamental frequency f 0 = 1/T 0 = 1/p Hz w 0 = 2 p/T 0 = 2 rad/s

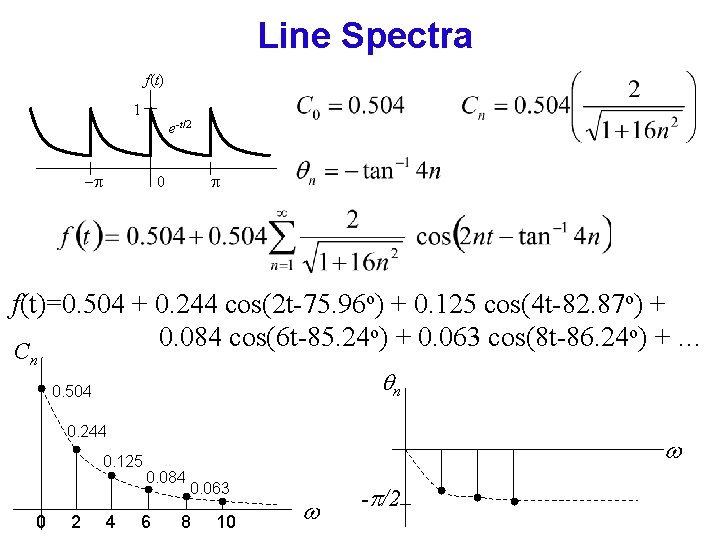
Line Spectra of x(t) • The amplitude spectrum of x(t) is defined as the plot of the magnitudes |Cn| versus • The phase spectrum of x(t) is defined as the plot of the angles versus • This results in line spectra • Bandwidth the difference between the highest and lowest frequencies of the spectral components of a signal.

Line Spectra f(t) 1 e-t/2 - 0 f(t)=0. 504 + 0. 244 cos(2 t-75. 96 o) + 0. 125 cos(4 t-82. 87 o) + 0. 063 cos(8 t-86. 24 o) + … 0. 084 cos(6 t-85. 24 C n n 0. 504 0. 244 0. 125 0 2 4 0. 084 6 0. 063 8 10 - /2

Line Spectra f(t)=0. 504 + 0. 244 cos(2 t-75. 96 o) + 0. 125 cos(4 t-82. 87 o) + 0. 063 cos(8 t-86. 24 o) + … 0. 084 cos(6 t-85. 24 C n n 0. 504 0. 244 0. 125 0 2 4 0. 084 6 0. 063 8 10 - /2

Matlab Tutorials • Tutorial 1 • Tutorial 2