Signaling Game Problems Signaling game Two players a

Signaling Game Problems

Signaling game. • Two players– a sender and receiver. • Sender knows his type. Receiver does not. It is not necessarily in the sender’s interest to tell the truth about his type. • Sender chooses an action (signal) that receiver observes. Action may depend on type. • Receiver takes an action given sender’s signal.

In Equilibrium • Receiver has beliefs about actions (signals) that will be taken by each type of sender. • Receiver chooses best action given senders’ signals and his beliefs about how signals are related to types. • Senders choose signals that maximize their payoffs given response of receivers. • Beliefs of receivers about senders’ types are confirmed.

Pooling and Separating • Pooling equilibrium—All types of senders send the same signal. • Separating equilibrium—Each type of sender sends a different signal. • Semi-separating equilibrium—Some, but not all types send same signals • In equilibrium beliefs of receivers about meaning of signals are confirmed by outcomes.
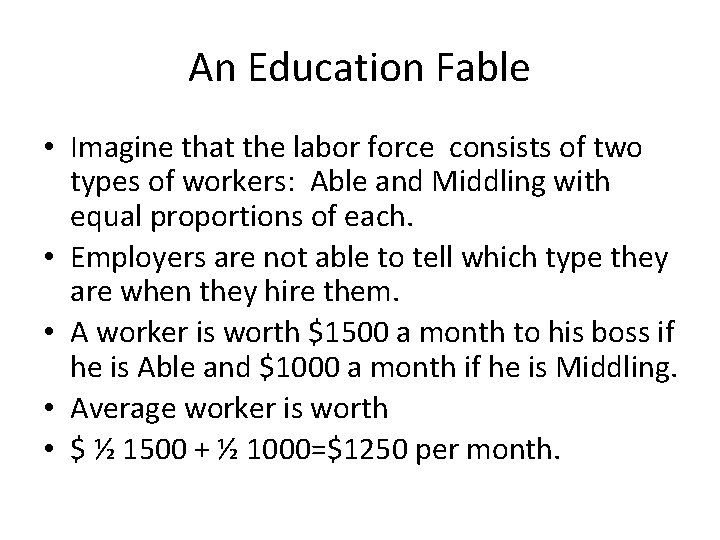
An Education Fable • Imagine that the labor force consists of two types of workers: Able and Middling with equal proportions of each. • Employers are not able to tell which type they are when they hire them. • A worker is worth $1500 a month to his boss if he is Able and $1000 a month if he is Middling. • Average worker is worth • $ ½ 1500 + ½ 1000=$1250 per month.

Competitive labor market • The labor market is competitive and since employers can’t tell the Able from the Middling, all laborers are paid a wage equal to the productivity of an average worker: $1250 per month.

Enter Professor Drywall

Drywall claims • My 10 -lecture course raises worker productivity by 20%!
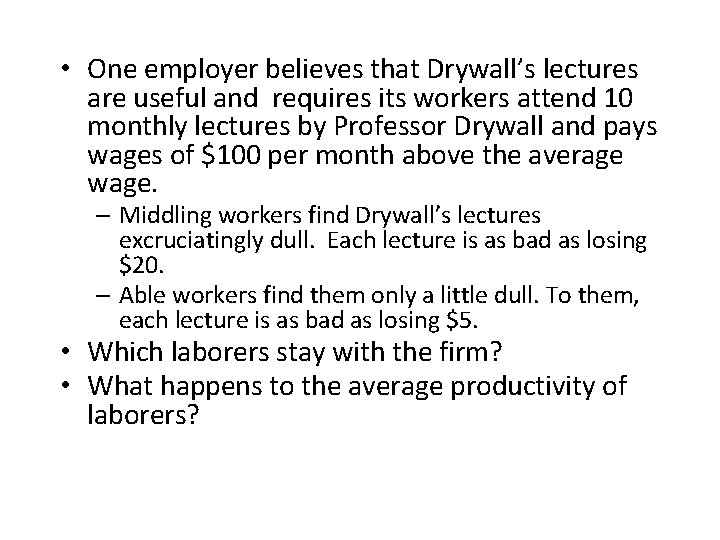
• One employer believes that Drywall’s lectures are useful and requires its workers attend 10 monthly lectures by Professor Drywall and pays wages of $100 per month above the average wage. – Middling workers find Drywall’s lectures excruciatingly dull. Each lecture is as bad as losing $20. – Able workers find them only a little dull. To them, each lecture is as bad as losing $5. • Which laborers stay with the firm? • What happens to the average productivity of laborers?

The outcome • Middling workers quit. Raise of $100 per month isn’t enough to compensate them for listening to Drywall. (They’d need $200. ) • Able workers stay. They don’t like the lectures, but $100 per month is enough to compensate for Drywall. (Drywall costs them $50. • Labor force is now all Able workers. Average productivity rises from $1250 to $1500.

Other firms see what happened • Professor Drywall shows the results of his lectures for productivity at the first firm. • Firms decide to pay wages of about $1500 for people who have taken Drywall’s course. • Now who will take Drywall’s course? • What will be the average productivity of workers who take his course? Do we have an equilibrium now?

A Drywall Premium? • Suppose those who take Drywall’s course get $1500 wage and those who don’t get $1250. • For Middling workers, a $250 wage premium is enough to make them take the course. • Able workers will also take the course. • Average productivity of those who take the course is now $ ½ 1000 + ½ 1500=1250. • Firm’s belief that those who take Drywall’s course are all Able is not confirmed. • This is not an equilibrium.

Professor Drywall responds • Professor Drywall is not discouraged. • He claims that the problem is that people have not heard enough lectures to learn his material. • Firms believe him and Drywall now makes his course last for 30 hours a month. • Firms pay almost $1500 wages for those who take his course and $1000 for those who do not.

A Separating Equilibrium • Able workers will prefer attending lectures and getting a wage of $1500, since to them the cost of attending the lectures is $5 x 30=$150 per month. • Middling workers will prefer not attending lectures since they can get $1000 if they don’t attend. Their cost of attending the lectures would be $20 x 30=$600, leaving them with a net of $900. • Firms’ beliefs are confirmed. Those who attend Drywall’s lectures are Able and those who don’t are Middling

But there is also a pooling equilibrium • Suppose that employers believe that Professor Drywall is a crackpot and that those who attended his lectures are no more productive than average. • They would not pay a premium for those who take Drywall’s course. • Nobody would take the course. • Employers’ beliefs are consistent with observation.

So there we are.

Example: Problem 1, Chapter 11 • • Quality Probability Value to Seller Value to Buyer Good Car q 10, 000 12, 000 Lemon 1 -q 6, 000 7, 000 A used car owner wants to sell his car. The fraction q of used cars are good and 1 -q are “lemons” Only the current owner (seller) knows if his car is good or a lemon. There are many buyers whose values are as above. • Sender is seller. Receivers are buyers. • Types of senders—good car owners, lemon owners • Possible actions taken by types—sell your used car or keep it.
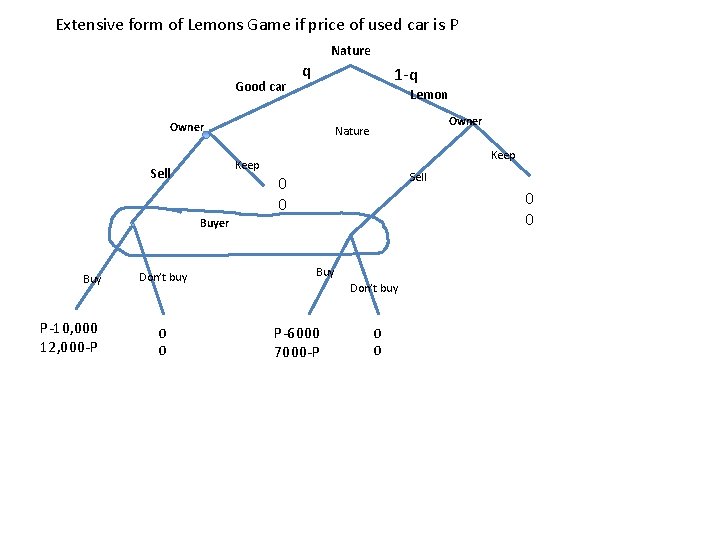
Extensive form of Lemons Game if price of used car is P Nature Good car q 1 -q Lemon Owner Keep Sell Owner Nature Keep Sell 0 0 Buyer Buy P-10, 000 12, 000 -P Don’t buy 0 0 Buy Don’t buy P-6000 7000 -P 0 0

Is there a pooling equlibrium? Quality Probability Value to Seller Value to Buyer Good Car q 10, 000 12, 000 Lemon 1 -q 6, 000 7, 000 • In a pooling equilibrium, both types of owners would sell their car. • Suppose buyers believe that all used car owners are selling. • A buyer gets a random draw of lemon or good car which is worth P=12, 000 q+7, 000(1 -q)=7, 000+5, 000 q. • Owners of good cars will sell their cars only if P≥ 10, 000. • So there can be a pooling equilibrium only if 7, 000+5, 000 q≥ 10, 000 • This implies q≥ 3/5. • So if q≥ 3/5, there is a pooling equilibrium at a price of about 7, 000+5 q. If q<3/5. there is no pooling equilibrium.
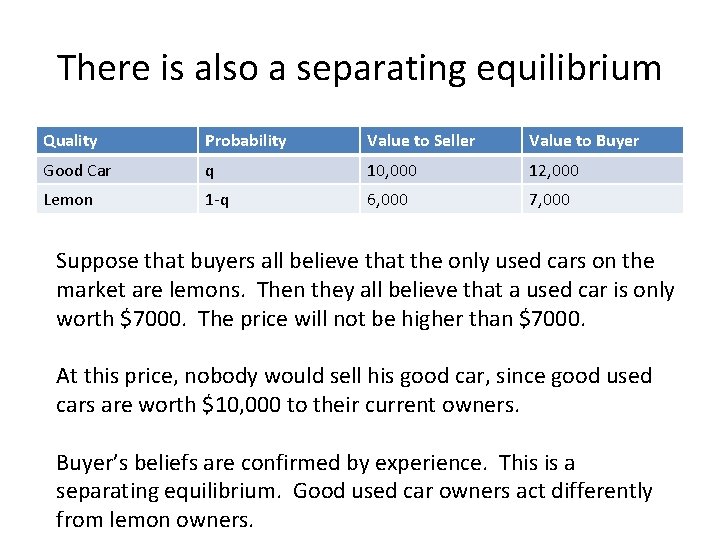
There is also a separating equilibrium Quality Probability Value to Seller Value to Buyer Good Car q 10, 000 12, 000 Lemon 1 -q 6, 000 7, 000 Suppose that buyers all believe that the only used cars on the market are lemons. Then they all believe that a used car is only worth $7000. The price will not be higher than $7000. At this price, nobody would sell his good car, since good used cars are worth $10, 000 to their current owners. Buyer’s beliefs are confirmed by experience. This is a separating equilibrium. Good used car owners act differently from lemon owners.

Pooling and separating • Notice that in this case, if q>3/5, there is both a separating and a pooling equilibrium. • In the pooling equilibrium, everybody believes that all used cars come to market and used cars sell for more than $10, 000. • In separating equilibrium, everybody believes that only lemons come to market. Used cars sell for $7000. • In either case, beliefs are confirmed by experience.

Signaling Equilibrium as Self-confirming Beliefs • Receiver has beliefs about probability distribution of types and how each type will act. • Receiver chooses a strategy that is a best response, given these beliefs and actions that the sender takes. • Each sender-type strategy is a best response, given the way receiver reacts. • Receiver’s beliefs about how each type will act are “confirmed” outcome.

Problem 11. 3 (Product Quality) • A product can be of either high or of low quality. Some retailers have high quality products, some have low quality. • Production cost is c for either type. • High quality items work with probability H and low quality items work with probability L. Consumer values a working item at V. • Value of a product to consumer is V if it works, 0 if it doesn’t.

Separating equilibrium with warranty • Find a separating equilibrium where high quality firm offers warranty, low quality firm offers no warranty and high quality firm charges a higher price than low quality firm.

Buyers’ beliefs and behavior • Suppose that buyer believes that items without warranty are of low quality and items with warranty are of high quality. • With these beliefs, – Buyer would pay up to LV for item without warranty. – Buyer would pay up to V for item with warranty.

Best response of High quality seller If Buyers believe that the only items without warranties are low quality: • An item with warranty could sell for (almost) V. An item with no warranty could sell for (almost) LV. • When a unit with warranty fails, seller has to give money back. For a high quality seller, expected cost of paying off warranties is (1 -H) (V+x) where x is the cost per unit of handling the repayment. • Expected profit per item sold with warranty is V-(1 -H)(V+x)-c=HV-(1 -H)x-c. • If sold without warranty, profit must be LV-c. • Selling with warranty gives higher profit if HV-(1 -H)x>LV.

Best response of Low Quality seller • Low quality seller could sell at price V with warranty, at price LV with no warranty. • Profit if it sells with warranty is V-(1 -L)(V+x)-c=LV-c-x(1 -L). • Profit per unit if it sells without warranty is LV-c • Selling without warranty is best response for Low quality seller.

An equilibrium • So if buyers believe that only the good items have guarantees: – the best response of high quality sellers is to price at V and offer a warranty – The best response of low quality sellers is to price at LV and offer no warranty. • This is an equilibrium. The buyers’ beliefs that only high quality sellers have warranties is confirmed by the way sellers act in response to these beliefs. (Self-confirming beliefs)

Why is does signaling “work” here? • It is cheaper for the high quality seller to offer a warranty than for a low quality seller. • Cost to high quality seller is (1 -H)(V+x). Cost to a low quality seller is (1 -L)(V+x)>(1 -H)(V+x). • So if having a warranty raises price you can charge from LV to V: – a warranty increases high quality seller’s revenue by (1 -L)V and his costs by (1 -H)(V+x)<(1 -L)V and so increases his profit. – a warranty increases low quality seller’s revenue by (1 -L)V and his costs by (1 -L)(V+x) so reduces his profit.

Problem 11. 6 (Advertising)

The setup • Nature determines a restaurant’s quality, high or low with probability ½ either way. • Production cost is $35 per meal for either type. • Price of a meal is fixed at $50 in either type. – Value of high quality to consumer is $85 – Value of low quality to consumer is $30. • A customer who goes to a high quality restaurant will come back a second time.

Find a Separating equilibrium • A restaurant can choose an amount A to spend on advertising. Customers observe A. • Find a separating equilibrium in which high quality restaurants spend A on advertising and low quality restaurants do not advertise.

Beliefs and Behavior • Suppose that customers believe that low quality restaurants spend less than A* on advertising and high quality restaurants spend at least A*. • With these beliefs, they will not go to a restaurant that spends less than A* and will go to one that spends A*.

What will restaurants do? • If consumers have these beliefs, low quality restaurants will have profits 50 -35 -A*=15 -A* if they spend A* on advertising and 0 if it spends less than A*. • For high quality restaurants, a consumer who comes once will come twice. So it will have profits 100 -70 -A*=30 -A* if it spends A* on advertising and 0 if it spends less than A*.

Suppose 15<A*<30 • Then if low quality restaurant spends A*, its profits will be 15 -A*<0, so it doesn’t pay a low quality restaurant to spend A* (or any money at all) on advertising). • If high quality restaurant spends A*, its profits will be 30 -A*>0. If it spends less its profit is 0, if it spends more its profits are less than 30 -A*. • So there is a separating equilibrium.

What makes for separation? • Because customers once attracted to a high quality business will return, advertising is more valuable to a high quality than to a low quality business and thus works as a signal in a separating equilibrium.

Other Customer Beliefs lead to Pooling equilibrium • Suppose that for some number A*<15, consumers believe that a restaurant that spends A* on average is equally likely to be good or bad, while any restaurant that spends less than A* is sure to be bad.

Response of Restaurants • All restaurants would find it profitable to advertise at level A*<15. • If they spent less they would get 0 profits. • So all would advertise at level A*. • Average payoff to customer from going to a restaurant that advertises at A* would be ½x 85+ ½x 35 -50=10, so customer would go to any restaurant that advertises at A*

Self-confirming beliefs • Note that there many different beliefs would be self-confirming. – In fact, for any A*<30, the belief that restaurants that spend less than A* are low quality is selfconfirming. – When A*>15, these beliefs lead to separating equilibrium – When A*<15, they lead to pooling equilibrium.

Problem 11. 5 • Students are of 3 types, High, medium, and low. Cost of getting a college degree to a student is 2 if high, 4 if medium, and 6 if low. • 1/6 of students are of high type, ½ of medium type, 1/3 are of low type. • Salaries for managers are 15, and 10 for clerks. • An employer has one clerk’s job to fill and one manager’s job to fill. Employer’s profits (net of wages) are 7 from hiring anyone as a clerk, 4 from hiring a low type as a manager, 6 from hiring a medium type as manager, 14 from hiring a high type as manager.
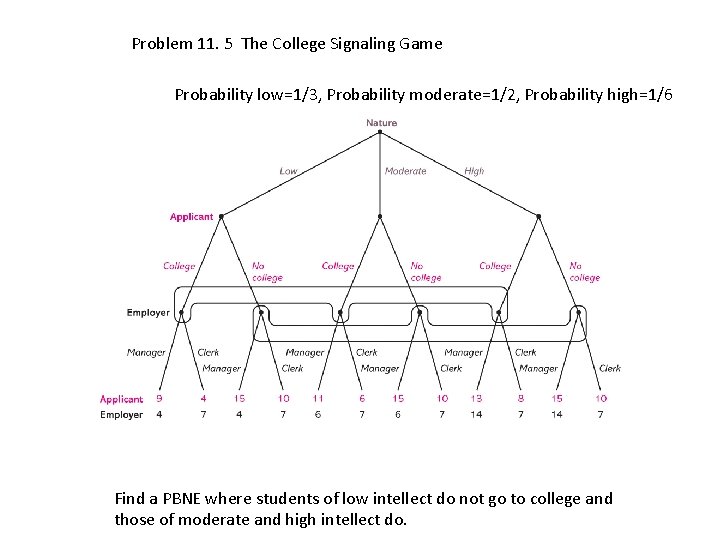
Problem 11. 5 The College Signaling Game Probability low=1/3, Probability moderate=1/2, Probability high=1/6 Find a PBNE where students of low intellect do not go to college and those of moderate and high intellect do.

Recall that the probability that an applicant is of low intellect is 1/3, probability of moderate intellect is 1/2 and probability of high intellect is 1/6. If the moderate and high intellect types go to college and the low intellect types do not, what proportion of those who go to college are of high intellect. A) B) C) D) E) 1/6 1/5 1/4 1/3 1/2

Conditional probability (Bayes’ Law) • P(H|C)=P(C and H) /P(C) =1/6÷(1/6+1/2)=1/4.

Beliefs and actions of Employer • Suppose employer believes that applicants of low intellect do not go to college and those of high and medium intellect do go. • Then if applicant has not gone to college, employer’s payoff is 4 for manager, 7 for clerk. • If applicant has gone to college, then employer believes he is of medium intellect with probability ¾ and high with probability 1/4 – Expected payoff from making him manager is 3/4 x 6+1/4 x 14=8 – Expected payoff from making him clerk is 7. • With these beliefs, employer will make college graduates managers, and non college applicants clerks.

Is this an equilibrium? • Will low intellect types choose not to go to college? Yes-they get payoff of 10 from no college and clerk and 9 from college and manager. • Will medium intellect types choose to go to college? Yes-they get payoff of 11 from college and manager and 10 from college and clerk. • Will high intellect types choose college? Yes, they get payoff of 13 from college and manager and 10 from no college and clerk.

Equilibrium • We see that when employer believes that low intellect types don’t go to college and all others do, then it is in the interest of low intellect types not to go to college and of high and medium intellect types to go to college. • So these employer beliefs are self-confirming.

Gazelle Signals: “I’m fast, Don’t chase me. ” This behavior is called “stotting”

Peacock signals, “I’m healthy, Mate with Me”

Enough signals for today
- Slides: 49