Signali i sustavi Vremenski diskretni signali i sustavi

Signali i sustavi Vremenski diskretni signali i sustavi

Uvod § Varijable diskretnog sustava u, x, y su funkcije diskretne nezavisne varijable tk Î T gdje je T Ì R prebrojiv skup. § Sve tk možemo poredati u niz, s rastućim indeksima k koje možemo interpretirati kao niz vremenskih trenutaka. § Niz definiramo kao funkciju t : Z ® T. § Vrijednost niza t na cijelom broju k označavamo s t(k) ili češće s tk. Opći član niza t je tk. § Nizove označavamo s. . . t-1 , t 0 , t 1 , t 2 , . . . ili {tk} , k Î Z ili (tk) , k Î Z 2

Uvod § Najjednostavniji i najvažniji slučaj niza t = {tk} je slučaj aritmetičkog niza kada je funkcija tk = T 0 k, gdje je T 0 po volji uzeta pozitivna konstanta. tk = T 0 k , k Î Z , T 0 - kvant vremena § Niz označavamo s u = {(tk , u(tk)), tk Î T } u = {uk} ili u = {u(k)} , k Î Z , ili u =. . . , u - 2 , u - 1 , u 0 , u 1 , u 2 , . . . ili u = {. . . , u - 2 , u - 1 , u 0 , u 1 , u 2 , . . . }. 3

Uvod § Npr. u =. . . , 3 -2 , 7 -1 , 50 , 91 , 62 , . . . § Ako su članovi u svom prirodnom redu, indekse možemo izostaviti i uzorak s k = 0 posebno označiti. § Npr. u =. . . , 3 , 7 , 5 , 9 , 6 , . . . § Kauzalan niz: uk = 0 za k < 0 , k Î Z u = {u 0 , u 1 , u 2 , . . . }. § Konačan niz: uk = 0 za k < 0 i k ³ K , k Î Z u = {u 0 , u 1 , . . . , u. K - 1}. § Periodičan niz s periodom N: uk + N = uk za k Î Z. 4

Osnovni nizovi § Jedinični niz (Niz s jediničnim članom ili uzorkom, Kroneckerov delta, d - niz). d =. . . , 0, 0, 1, 0, 0, . . . 5

Osnovni nizovi § Jedinična stepenica (Heavisideov niz) S =. . . , 0, 0, 1, 1, 1, . . . § Osnovni kauzalni niz. § Množenjem nekauzalnog niza s Heavisideovim nizom on postaje kauzalan. 6

Osnovni nizovi § Jedinična kosina L =. . . , 0, 0, 1, 2, 3, 4, . . . 7

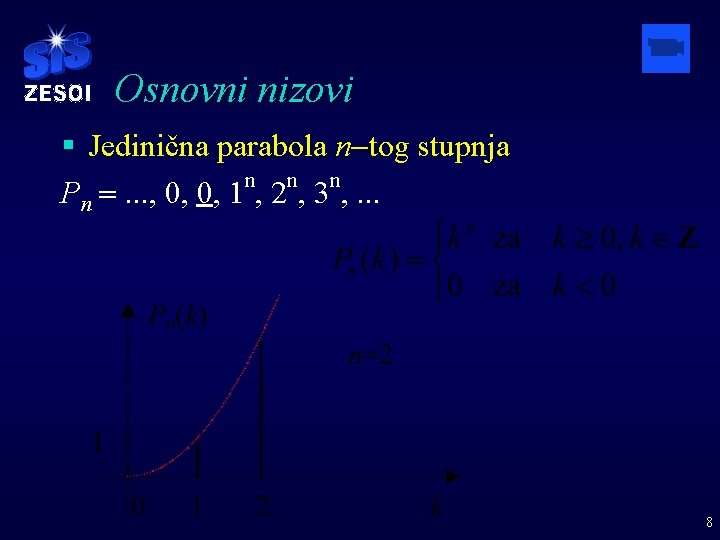
Osnovni nizovi § Jedinična parabola n-tog stupnja n n n Pn =. . . , 0, 0, 1 , 2 , 3 , . . . 8

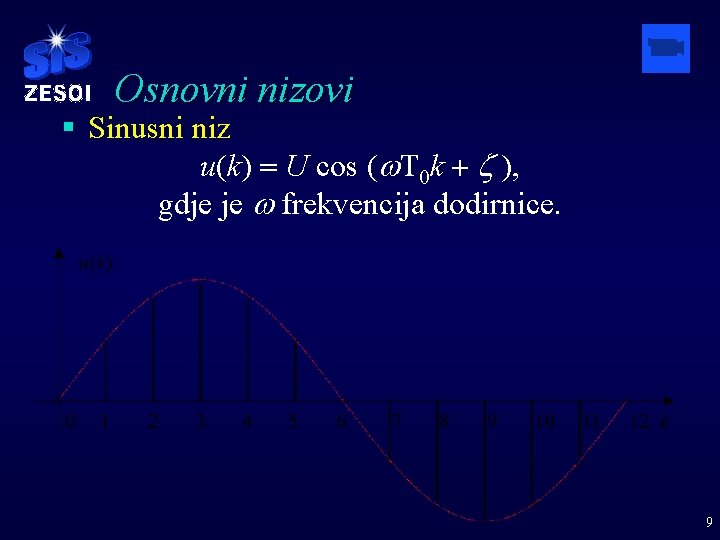
Osnovni nizovi § Sinusni niz u(k) = U cos (w. T 0 k + z ), gdje je w frekvencija dodirnice. 9

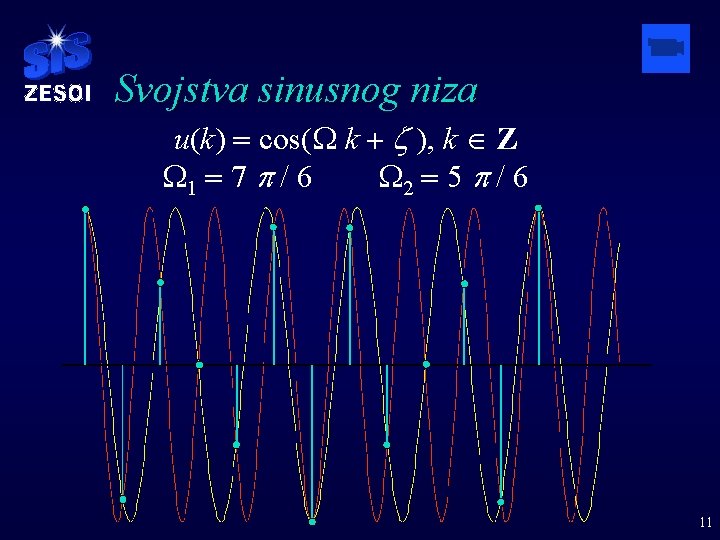
Svojstva sinusnog niza u(k) = U cos (Wk + z ), k Î Z, U - amplituda, z - faza, W = w. T 0 - korak argumenta u radijanima analogan frekvenciji. § Za W = p + D izlazi u(k) = cos(p + D)k = cos(-2 p + D)k = cos(-p + D)k = cos(p - D)k. § Iz raspoloživog niza se ne može razlikovati da li je frekvencija dodirnice W 1 = p + D ili W 2 = p - D. 10

Svojstva sinusnog niza u(k) = cos(W k + z ), k Î Z W 1 = 7 p / 6 W 2 = 5 p / 6 11

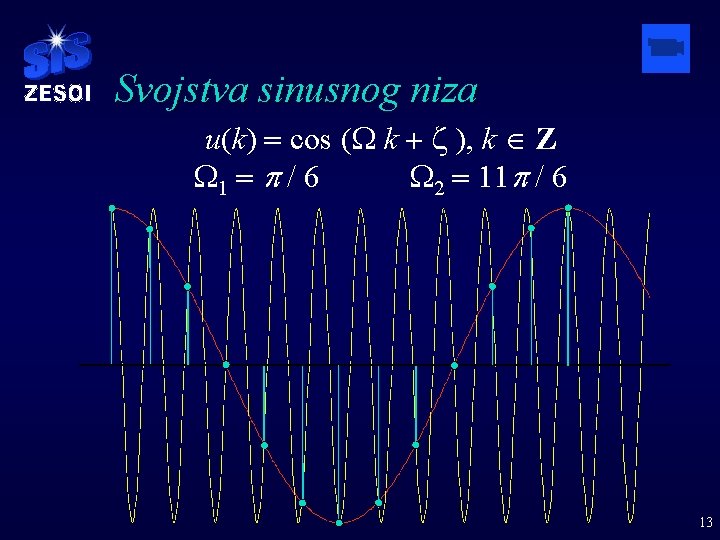
Svojstva sinusnog niza § Za W = 2 p - D izlazi u(k) = cos(2 p - D)k = cos(-Dk) = cos Dk. § Iz raspoloživog niza se ne može razlikovati da li je frekvencija dodirnice W 1 = 2 p - D ili W 2 = D. 12

Svojstva sinusnog niza u(k) = cos (W k + z ), k Î Z W 1 = p / 6 W 2 = 11 p / 6 13

Svojstva sinusnog niza § Vidi se da se iz ovog niza ne može razlikovati frekvencija W 1 od bilo koje Wn = W 1 + 2 np , n Î Z jer je cos[(W 1 + 2 np)k] = cos(W 1 k + 2 nkp) = cos(W 1 k) n, k Î Z. § Da bi se W mogao odrediti jednoznačno iz niza moramo biti sigurni da je |W| < p , odnosno w < p / T 0 ili 2 f < 1 / T 0. 14

Osnovni nizovi § Eksponencijalni niz u(k) = qk , q Î R q<1 q>1 q=1 q = -1 - padajući niz - rastući niz - konstantni niz - alternirajući niz 15

Svojstva eksponencijalnog niza § Eksponencijalni niz ovisno od kompleksnog parametra q ili zn može poprimiti različite oblike, a pogotovo ako nekoliko elementarnih nizova znk formira linearnu kombinaciju. § Za k Î Z nizovi su nekauzalnog oblika, a za k Î N su kauzalni, pri čemu z može biti realan, imaginaran ili konjugirano kompleksan. 16

Osnovne operacije na nizovima i elementi diskretnog sustava § Zbrajanje nizova Zbroj dva niza y = u + v ili {y(k)} = {u(k)} + {v(k)} je niz s općim članom y(k) = u(k) + v(k) za svaki k Î Z. § Produkt nizova Produkt dva niza y = uv ili {y(k)} = {u(k)} {v(k)} je niz s općim članom y(k) = u(k)v(k) za svaki k Î Z. 17

Osnovne operacije na nizovima i elementi diskretnog sustava § Množenje s konstantom y = a u ili {y(k)} = a{u(k)} = {a u(k)} y(k) = a u(k) za svaki k Î Z. § Funkcijski blok y = f (u) ili {y(k)} = f [{u(k)}] y(k) = f [u(k)] za svaki k Î Z. 18

Osnovne memorijske i predikcijske operacije § Pomak niza - jedinični pomak daje iz ulaznog niza, niz pomaknut za jedan korak. unaprijed (predikcija) y = E u ili {y(k)} = E {u(k)}, y(k) = (Eu)(k), y(k) = u(k + 1) k ³ 0. unatrag (kašnjenje i pamćenje) y = E-1 u ili {y(k)} = E-1{u(k)}, y(k) = (E-1 u)(k), y(k) = u(k - 1) k > 0. 19

Pomak niza § Operacija pomaka niza unaprijed traži nekauzalan sustav pa je neostvariva u realnim sustavima. § Zato se služimo redovito jedinicama za kašnjenje, odnosno operacijom E-1. 20

Osnovne memorijske i predikcijske operacije § Diferencija niza y = D u ili {y(k)} = D {u(k)}, y = Ñu ili {y(k)} = Ñ{u(k)}, y(k) = (Du)(k) = u(k + 1) - u(k), y(k) = (Ñu)(k) = u(k) - u(k - 1), {y(k)} = (E - 1){u(k)}. {y(k)} = (1 - E-1){u(k)}. 21

Osnovne memorijske i predikcijske operacije § Diferencija višeg reda 22

Osnovne memorijske i predikcijske operacije § Akumulacija niza § Antidiferencijski operator D-1 daje niz {y(k)} = D-1{u(k)} takav da je D{y(k)} = {u(k)}. § Može se pokazati da vrijedi § Za slučaj kauzalnih signala § Prema tome: 23

Model vrem. diskretnog sustava § Bezmemorijski sustav y(k) = f [u(k)]. § Memorijski sustav y(k) = F(x(k 0), u(k 0, k] ) za k > k 0. § Bezmemorijski dio: v(k) = f (x(k), u(k)), y(k) = g (x(k), u(k)). § Memorijski dio: x(k) = F (x(k 0), v(k 0 , k]). 27

Model vrem. diskretnog sustava § Posebno važan memorijski element u memorijskom podsustavu je element jediničnog kašnjenja. u(k), x(k), y(k) - vektori sustava § Jednadžbe sustava: x(k + 1) = f (x(k), u(k)), y(k) = g (x(k), u(k)). 28

Model vrem. diskretnog sustava § Veza s kontinuiranim sustavom u slučaju da se derivacija aproksimira s diferencijom x(k + 1) = x(k) + Tf(x(k), u(k)). § linearni sustav x(k + 1) = (I + TA)x(k) + TBu(k), x(k + 1) = Adx(k) + TBu(k). 29