Signal Processing First Lecture 21 Frequency Response of

Signal Processing First Lecture 21 Frequency Response of Continuous-Time Systems 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 1

READING ASSIGNMENTS § This Lecture: § Chapter 10, all § Other Reading: § Recitation: Ch. 10 all, start Ch 11 § Next Lecture: Chapter 11 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 3

LECTURE OBJECTIVES § Review of convolution § THE operation for LTI Systems § Complex exponential input signals § Frequency Response § Cosine signals § Real part of complex exponential § Fourier Series thru H(jw) § These are Analog Filters 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 4

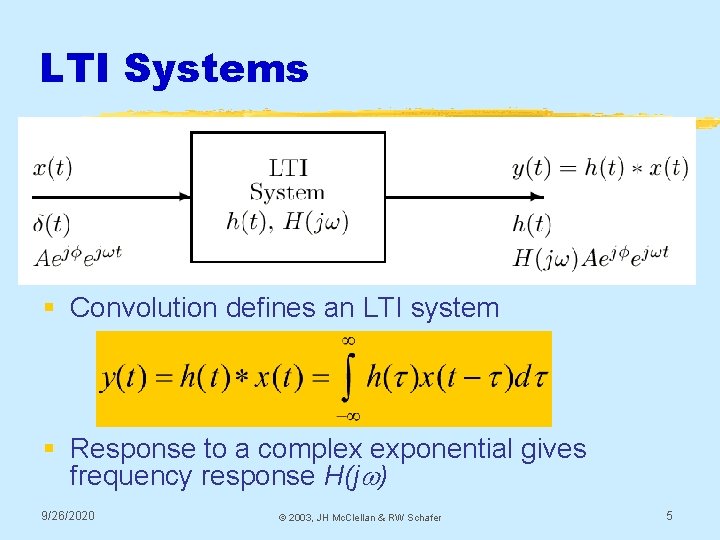
LTI Systems § Convolution defines an LTI system § Response to a complex exponential gives frequency response H(jw) 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 5

Thought Process #1 § SUPERPOSITION (Linearity) § Make x(t) a weighted sum of signals § Then y(t) is also a sum—same weights • But DIFFERENT OUTPUT SIGNALS usually § Use SINUSOIDS • “SINUSOID IN GIVES SINUSOID OUT” § Make x(t) a weighted sum of sinusoids § Then y(t) is also a sum of sinusoids § Different Magnitudes and Phase § LTI SYSTEMS: Sinusoidal Response 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 6

Thought Process #2 § SUPERPOSITION (Linearity) § Make x(t) a weighted sum of signals § Use SINUSOIDS § Any x(t) = weighted sum of sinusoids § HOW? Use FOURIER ANALYSIS INTEGRAL § To find the weights from x(t) § LTI SYSTEMS: § Frequency Response changes each sinusoidal component 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 7

Complex Exponential Input Frequency Response 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 8

When does H(jw) Exist? § When is ? § Thus the frequency response exists if the LTI system is a stable system. 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 9

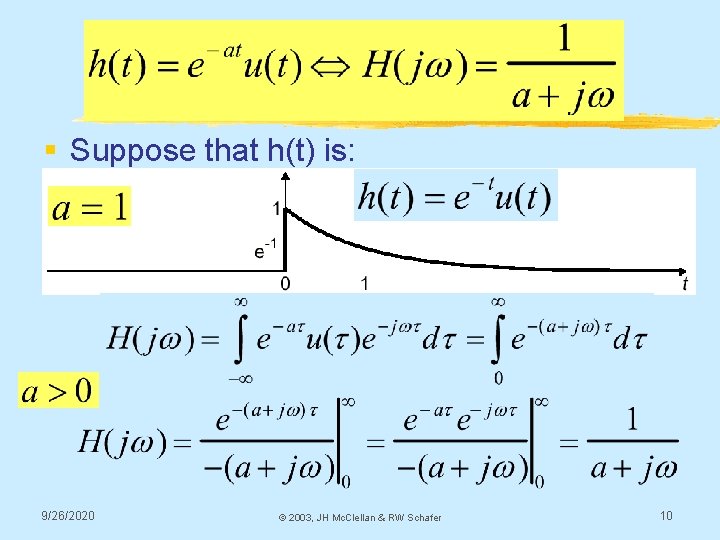
§ Suppose that h(t) is: 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 10

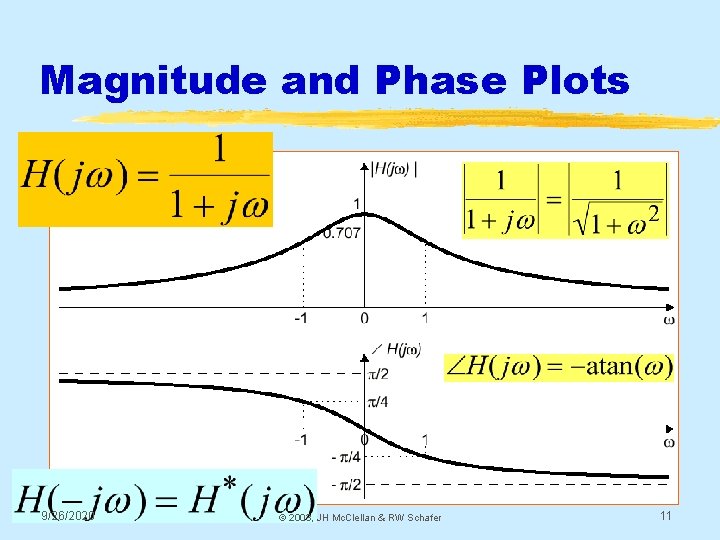
Magnitude and Phase Plots 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 11

Freq Response of Integrator? § Impulse Response § h(t) = u(t) § NOT a Stable System § Frequency response H(jw) does NOT exist Need another term “Leaky” Integrator (a is small) Cannot build a perfect Integral 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 12

Ideal Delay: 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 13

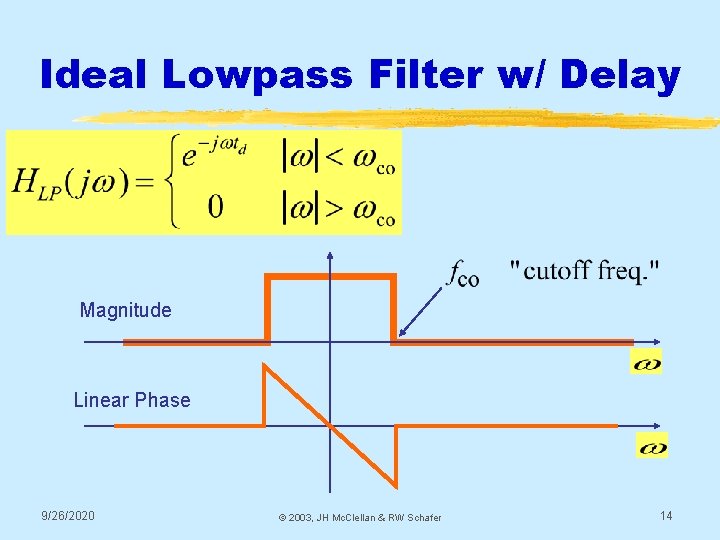
Ideal Lowpass Filter w/ Delay Magnitude Linear Phase 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 14

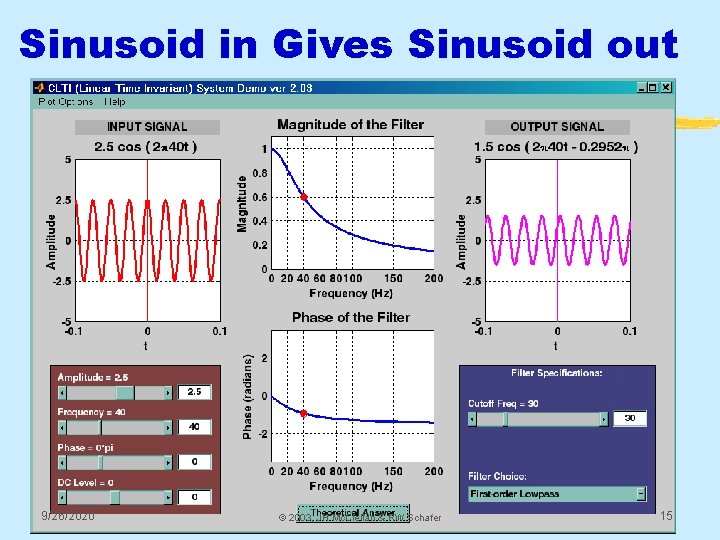
Sinusoid in Gives Sinusoid out 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 15

Example: Ideal Low Pass 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 16

Cosine Input 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 17

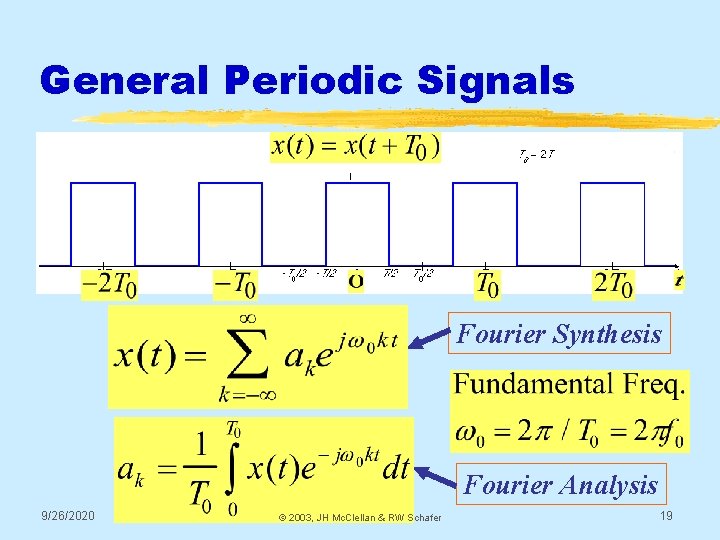
Review Fourier Series § ANALYSIS § Get representation from the signal § Works for PERIODIC Signals § Fourier Series § INTEGRAL over one period 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 18

General Periodic Signals Fourier Synthesis Fourier Analysis 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 19

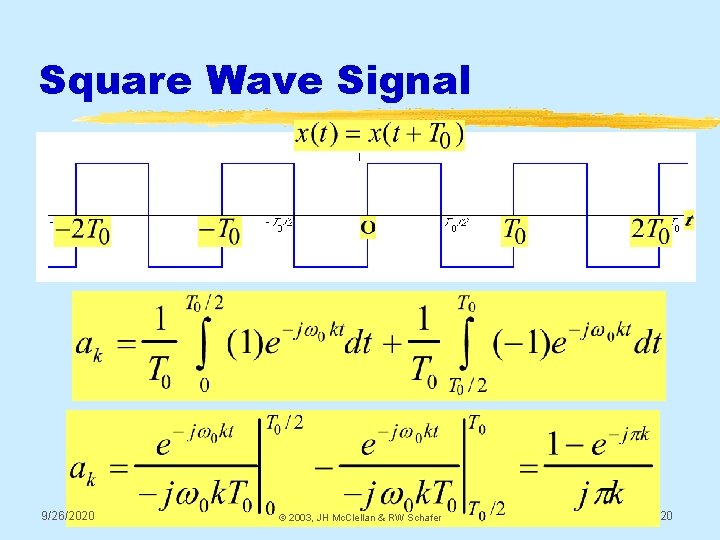
Square Wave Signal 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 20

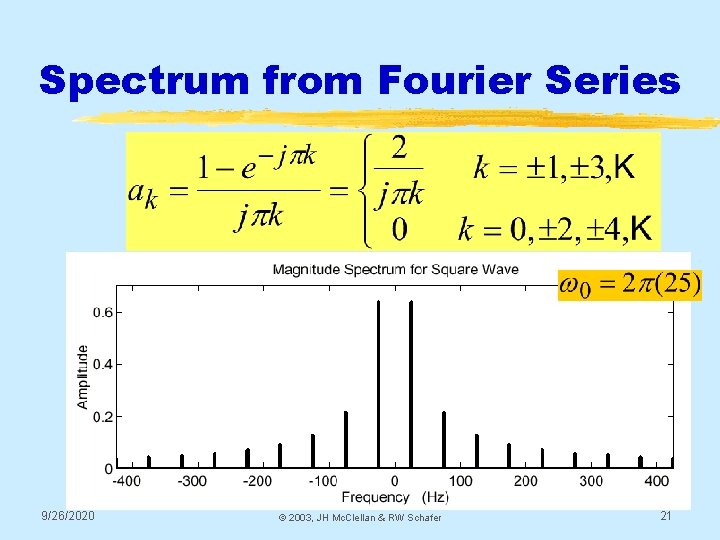
Spectrum from Fourier Series 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 21

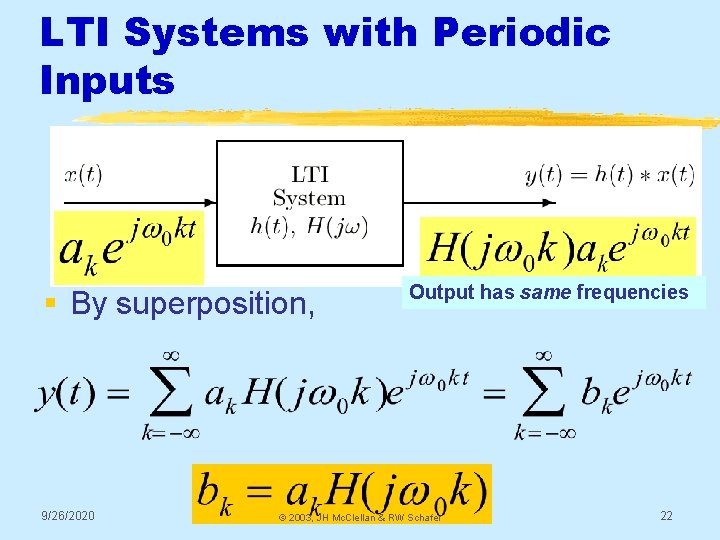
LTI Systems with Periodic Inputs § By superposition, 9/26/2020 Output has same frequencies © 2003, JH Mc. Clellan & RW Schafer 22

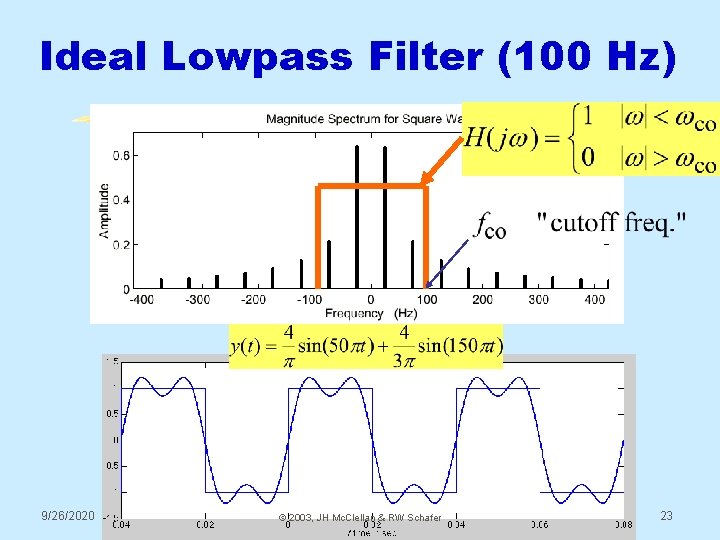
Ideal Lowpass Filter (100 Hz) 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 23

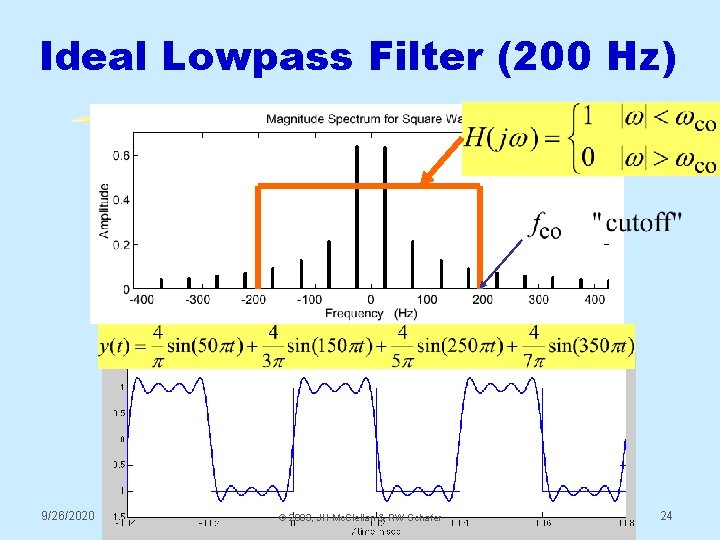
Ideal Lowpass Filter (200 Hz) 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 24

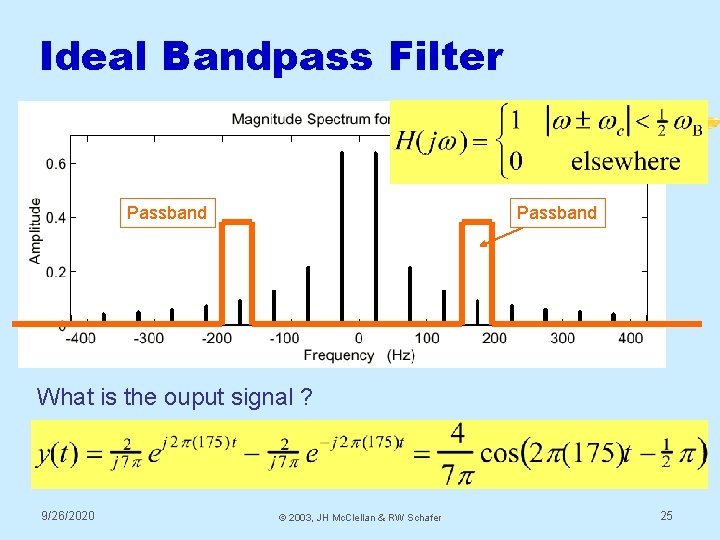
Ideal Bandpass Filter Passband What is the ouput signal ? 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 25

Example 9/26/2020 © 2003, JH Mc. Clellan & RW Schafer 26