Signal Processing First Lecture 20 Convolution ContinuousTime 9172020











- Slides: 18

Signal Processing First Lecture 20 Convolution (Continuous-Time) 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 1

READING ASSIGNMENTS § This Lecture: § Chapter 9, Sects. 9 -6, 9 -7, and 9 -8 § Other Reading: § Recitation: Ch. 9, all § Next Lecture: Start reading Chapter 10 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 2

LECTURE OBJECTIVES § Evaluating convolutions § Examples § Impulses § LTI Systems § Stability and causality § Cascade and parallel connections 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 3

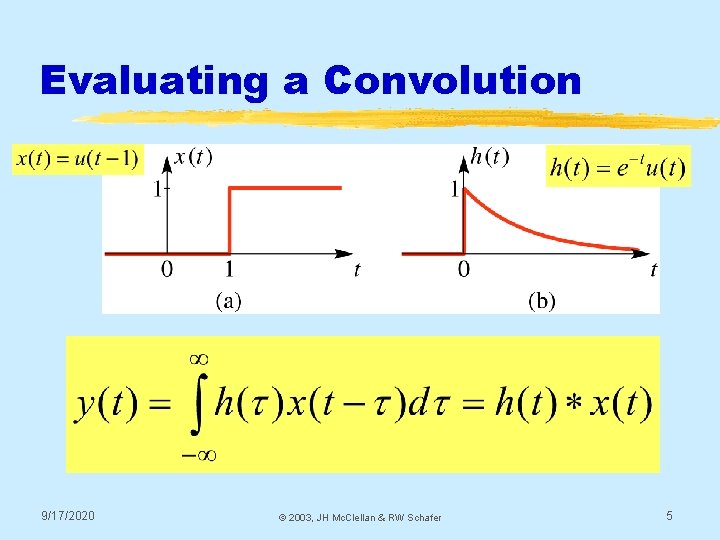
Linear and Time-Invariant (LTI) Systems § If a continuous-time system is both linear and time-invariant, then the output y(t) is related to the input x(t) by a convolution integral where h(t) is the impulse response of the system. 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 4

Evaluating a Convolution 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 5

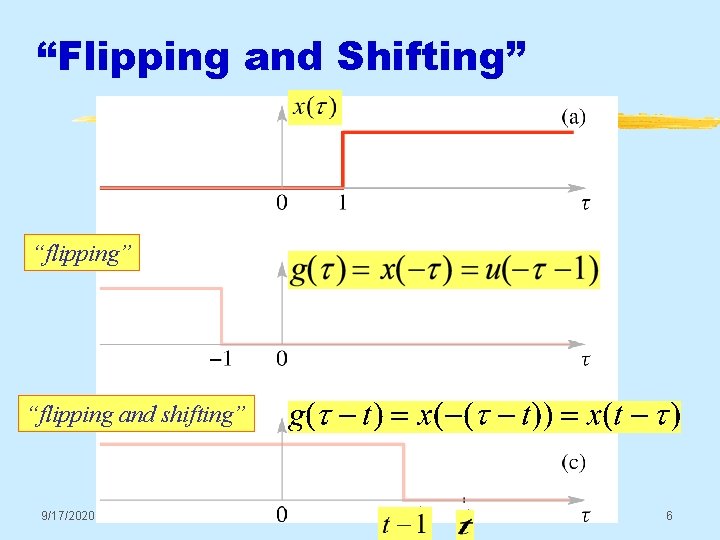
“Flipping and Shifting” “flipping and shifting” 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 6

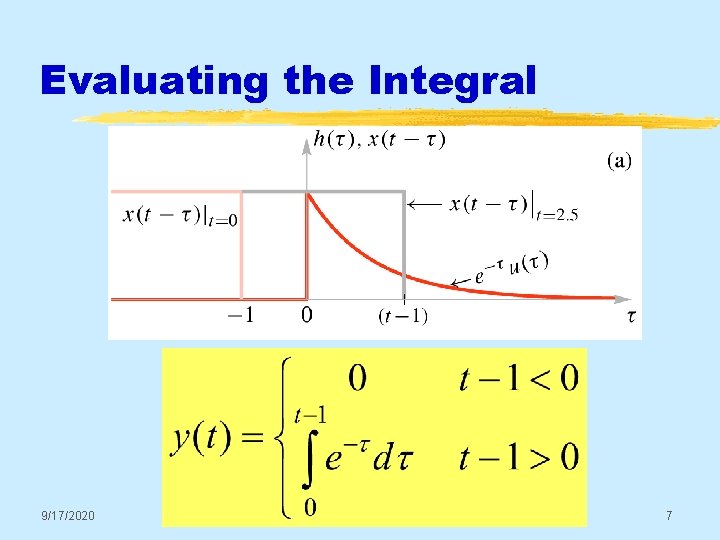
Evaluating the Integral 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 7

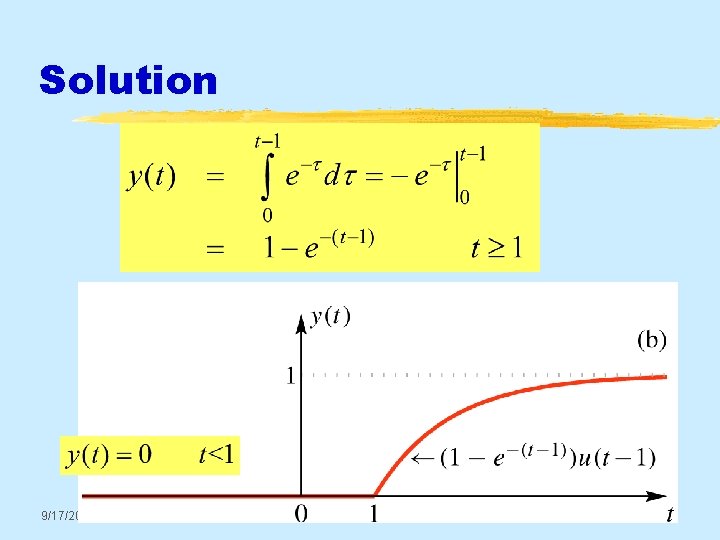
Solution 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 8

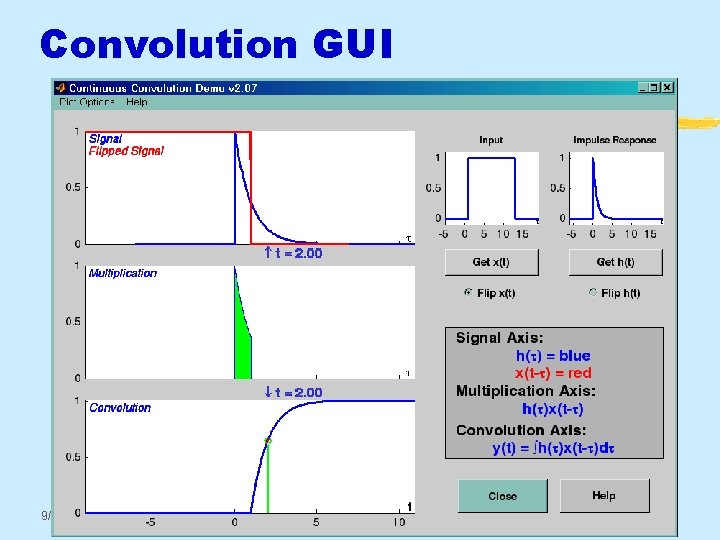
Convolution GUI 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 9

General Convolution Example 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 10

Special Case: u(t) 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 11

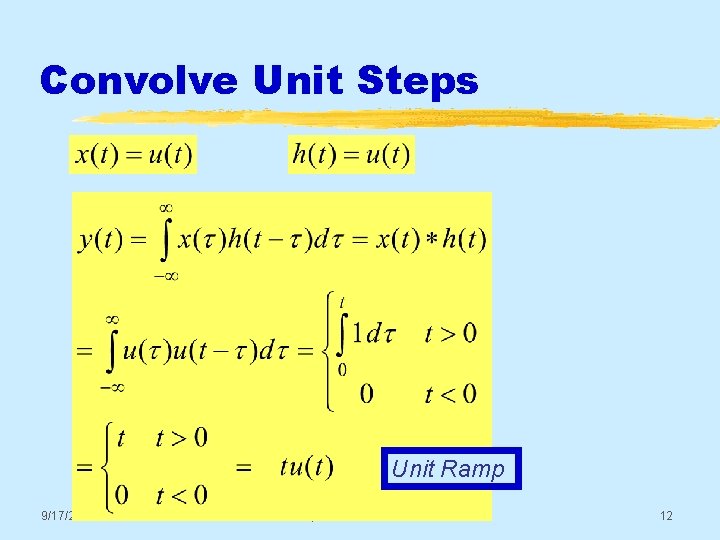
Convolve Unit Steps Unit Ramp 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 12

Convolution is Commutative 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 13

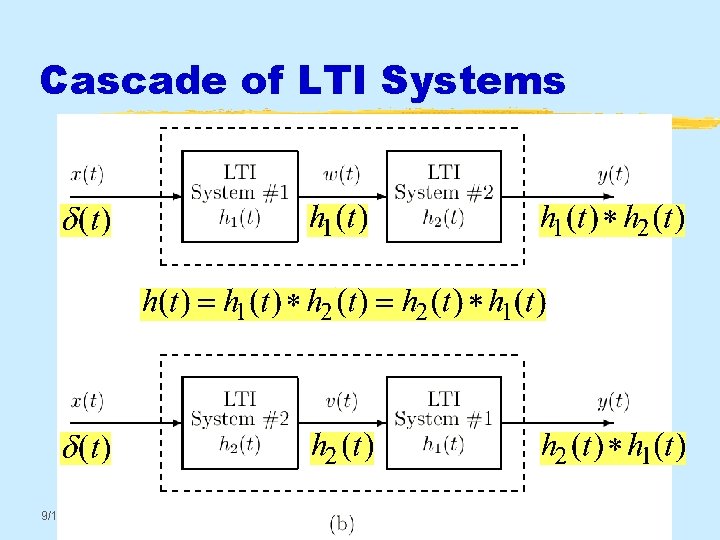
Cascade of LTI Systems 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 14

Stability § A system is stable if every bounded input produces a bounded output. § A continuous-time LTI system is stable if and only if 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 15

Causal Systems § A system is causal if and only if y(t 0) depends only on x(t) for t< t 0. § An LTI system is causal if and only if 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 16

Convolution is Linear § Substitute x(t)=ax 1(t)+bx 2(t) Therefore, convolution is linear. 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 17

Convolution is Time-Invariant § Substitute x(t-t 0) 9/17/2020 © 2003, JH Mc. Clellan & RW Schafer 18