Signal Processing First Lecture 18 3 Domains for

Signal Processing First Lecture 18 3 -Domains for IIR 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 1

READING ASSIGNMENTS § This Lecture: § Chapter 8, all § Other Reading: § Recitation: Ch. 8, all § POLES & ZEROS § Next Lecture: Chapter 9 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 3

LECTURE OBJECTIVES § SECOND-ORDER IIR FILTERS § TWO FEEDBACK TERMS § H(z) can have COMPLEX POLES & ZEROS § THREE-DOMAIN APPROACH § BPFs have POLES NEAR THE UNIT CIRCLE 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 4

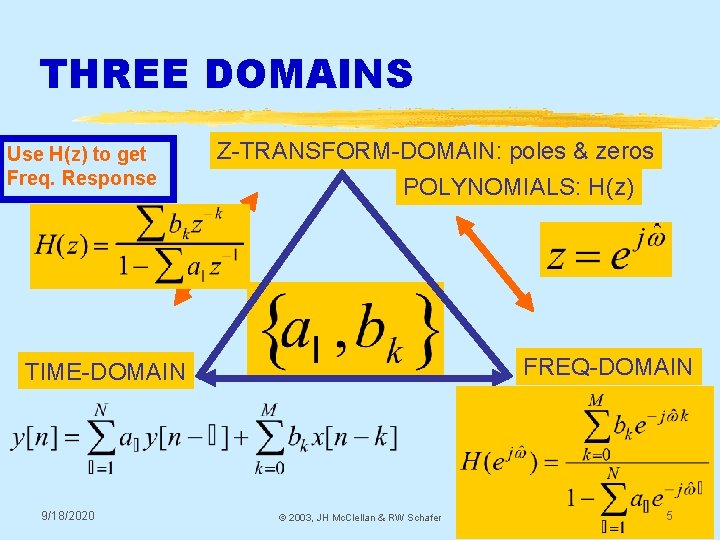
THREE DOMAINS Use H(z) to get Freq. Response Z-TRANSFORM-DOMAIN: poles & zeros POLYNOMIALS: H(z) FREQ-DOMAIN TIME-DOMAIN 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 5

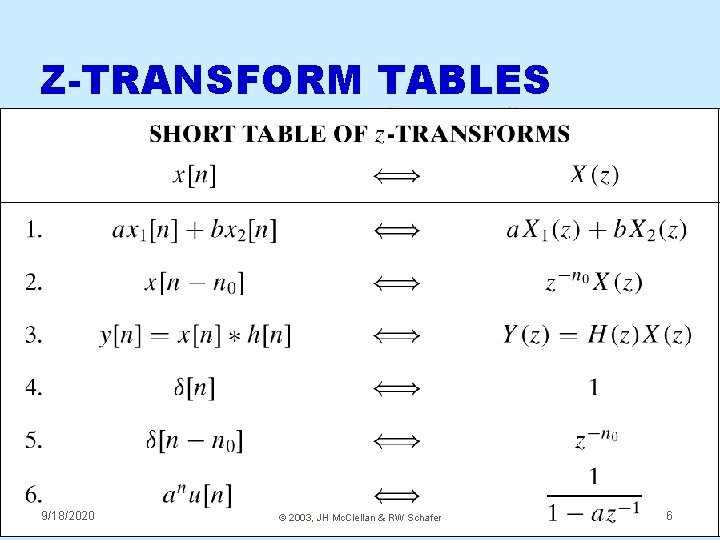
Z-TRANSFORM TABLES 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 6

SECOND-ORDER FILTERS § Two FEEDBACK TERMS 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 7

MORE POLES § Denominator is QUADRATIC § 2 Poles: REAL § or COMPLEX CONJUGATES 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 8

TWO COMPLEX POLES § Find Impulse Response ? § Can OSCILLATE vs. n § “RESONANCE” § Find FREQUENCY RESPONSE § Depends on Pole Location § Close to the Unit Circle? § Make BANDPASS FILTER 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 9

2 nd ORDER EXAMPLE 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 10

h[n]: Decays & Oscillates “PERIOD”=6 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 11

2 nd ORDER Z-transform PAIR GENERAL ENTRY for z-Transform TABLE 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 12

2 nd ORDER EX: n-Domain aa bb nn hh HH = = = 9/18/2020 [ 1, -0. 9, 0. 81 ]; [ 1, -0. 45 ]; -2: 19; filter( bb, aa, (nn==0) ); freqz( bb, aa, [-pi, pi/100: pi] ); © 2003, JH Mc. Clellan & RW Schafer 13

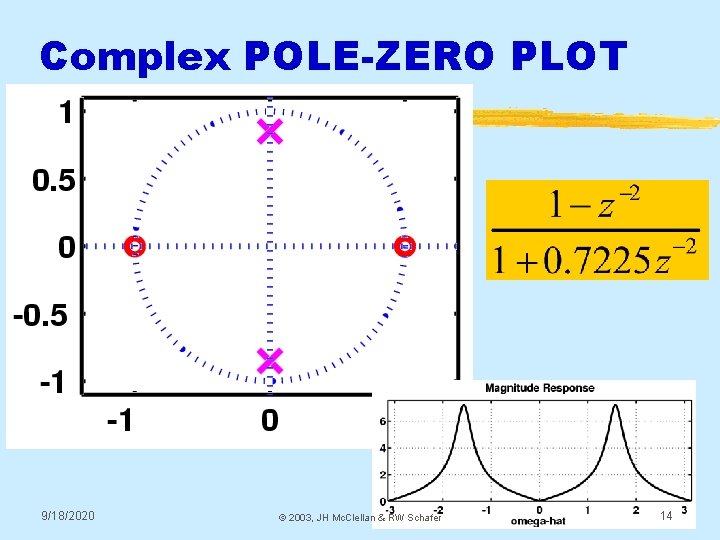
Complex POLE-ZERO PLOT 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 14

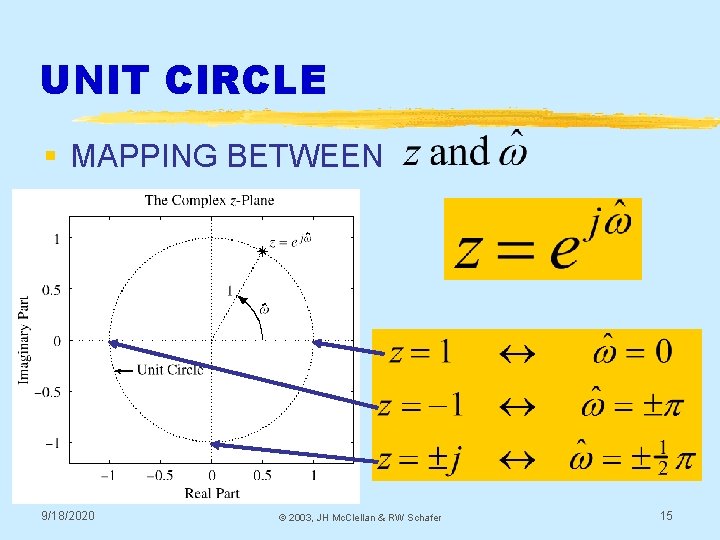
UNIT CIRCLE § MAPPING BETWEEN 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 15

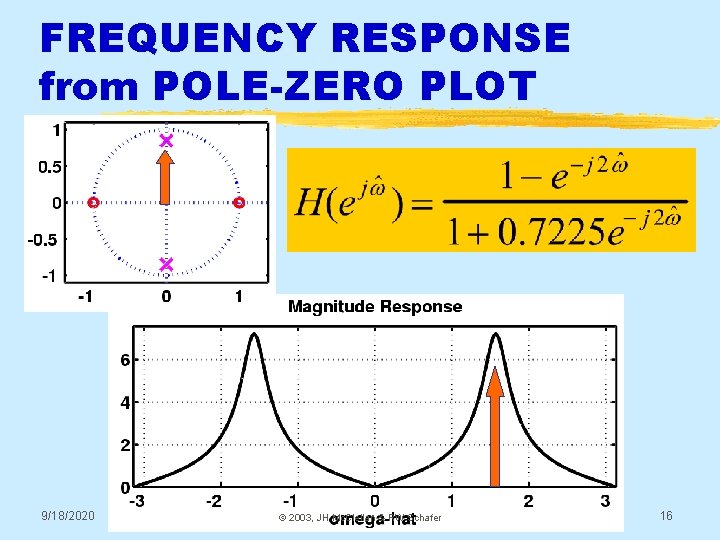
FREQUENCY RESPONSE from POLE-ZERO PLOT 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 16

h[n]: Decays & Oscillates “PERIOD”=6 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 17

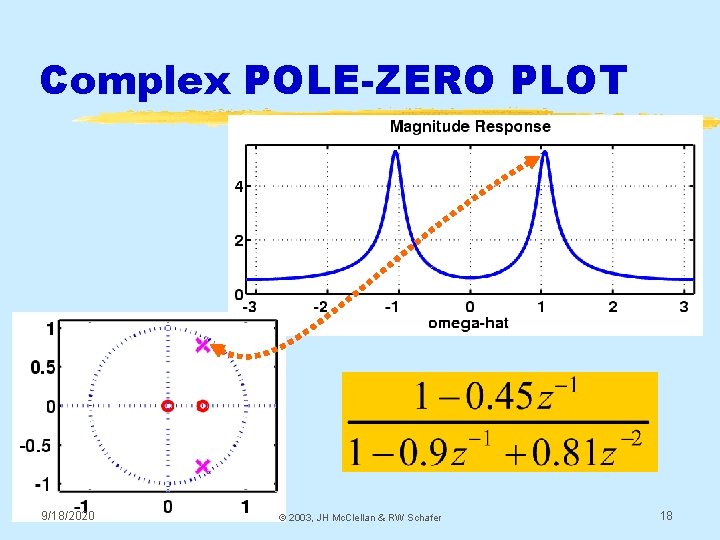
Complex POLE-ZERO PLOT 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 18

h[n]: Decays & Oscillates “PERIOD”=12 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 19

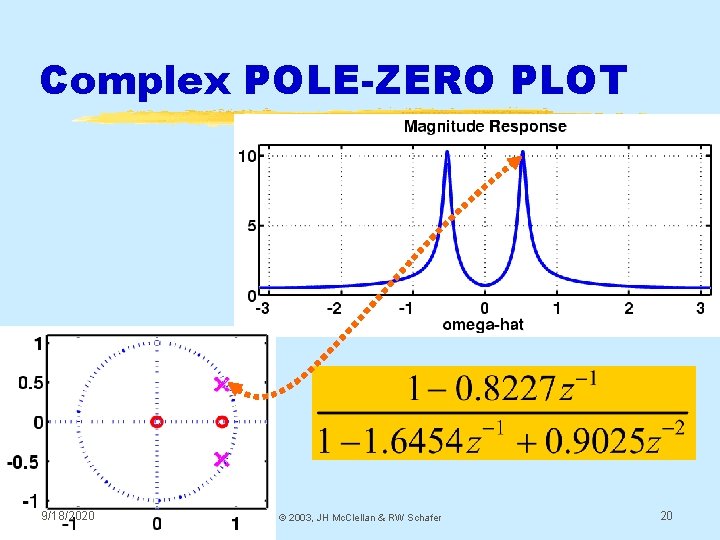
Complex POLE-ZERO PLOT 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 20

3 DOMAINS MOVIE: IIR POLE MOVES H(z) H(w) h[n] 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 21

THREE INPUTS § Given: § Find the output, y[n] § When 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 22

SINUSOID ANSWER § Given: § The input: § Then y[n] 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 23

Step Response Partial Fraction Expansion 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 27

Step Response 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 28

Stability § Nec. & suff. condition: Pole must be Inside unit circle 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 29

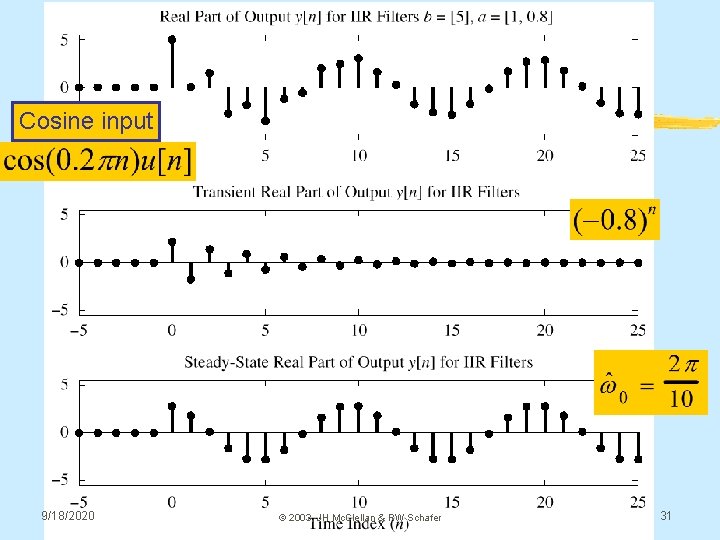
SINUSOID starting at n=0 § We’ll look at an example in MATLAB § cos(0. 2 pn) § Pole at – 0. 8, so an is (– 0. 8) n § There are two components: § TRANSIENT § Start-up region just after n=0; (– 0. 8) n § STEADY-STATE § Eventually, y[n] looks sinusoidal. § Magnitude & Phase from Frequency Response 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 30

Cosine input 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 31

STABILITY § When Does the TRANSIENT DIE OUT ? 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 32

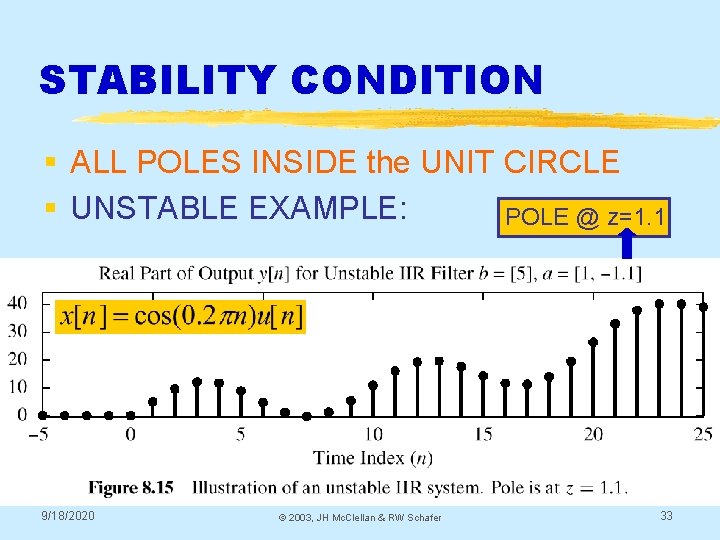
STABILITY CONDITION § ALL POLES INSIDE the UNIT CIRCLE § UNSTABLE EXAMPLE: POLE @ z=1. 1 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 33

BONUS QUESTION § Given: § The input is § Then find y[n] 9/18/2020 © 2003, JH Mc. Clellan & RW Schafer 34