Signal Processing First Lecture 14 Z Transforms Introduction

Signal Processing First Lecture 14 Z Transforms: Introduction 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 1

READING ASSIGNMENTS § This Lecture: § Chapter 7, Sects 7 -1 through 7 -5 § Other Reading: § Recitation: Ch. 7 § CASCADING SYSTEMS § Next Lecture: Chapter 7, 7 -6 to the end 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 3

LECTURE OBJECTIVES § INTRODUCE the Z-TRANSFORM § Give Mathematical Definition § Show the H(z) POLYNOMIAL simplifies analysis § CONVOLUTION is SIMPLIFIED ! § Z-Transform can be applied to § FIR Filter: h[n] --> H(z) § Signals: x[n] --> X(z) 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 4

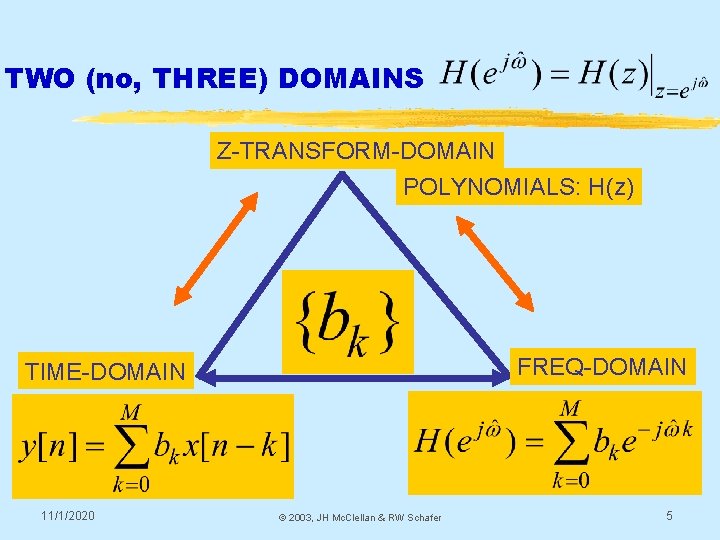
TWO (no, THREE) DOMAINS Z-TRANSFORM-DOMAIN POLYNOMIALS: H(z) FREQ-DOMAIN TIME-DOMAIN 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 5

TRANSFORM CONCEPT § Move to a new domain where § OPERATIONS are EASIER & FAMILIAR § Use POLYNOMIALS § TRANSFORM both ways § x[n] ---> X(z) (into the z domain) § X(z) ---> x[n] (back to the time domain) 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 6

“TRANSFORM” EXAMPLE § Equivalent Representations x[n] y[n] 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 7

Z-TRANSFORM IDEA § POLYNOMIAL REPRESENTATION 11/1/2020 x[n] y[n] © 2003, JH Mc. Clellan & RW Schafer 8

Z-Transform DEFINITION § POLYNOMIAL Representation of LTI SYSTEM: § EXAMPLE: APPLIES to Any SIGNAL POLYNOMIAL in z-1 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 9

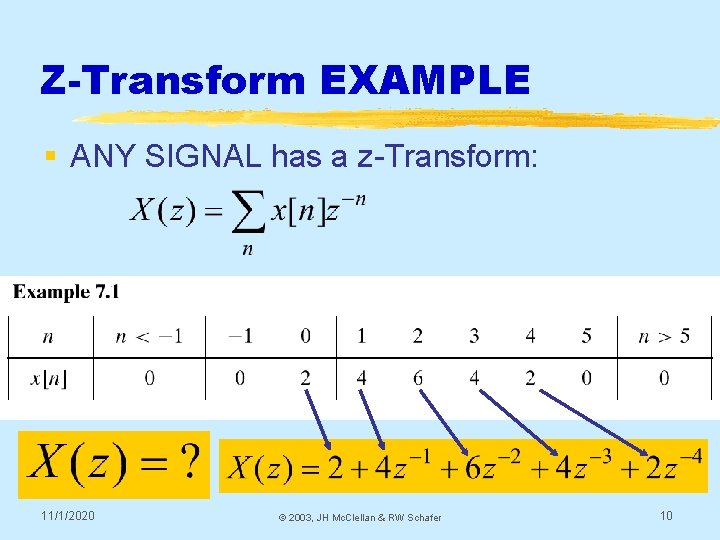
Z-Transform EXAMPLE § ANY SIGNAL has a z-Transform: 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 10

EXPONENT GIVES TIME LOCATION 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 11

Z-Transform of FIR Filter § CALLED the SYSTEM FUNCTION § h[n] is same as {bk} SYSTEM FUNCTION FIR DIFFERENCE EQUATION 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer CONVOLUTION 12

Z-Transform of FIR Filter § Get H(z) DIRECTLY from the {bk} § Example 7. 3 in the book: 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 13

Ex. DELAY SYSTEM § UNIT DELAY: find h[n] and H(z) x[n] y[n] = x[n-1] x[n] 11/1/2020 y[n] © 2003, JH Mc. Clellan & RW Schafer 14

DELAY EXAMPLE § UNIT DELAY: find y[n] via polynomials § x[n] = {3, 1, 4, 1, 5, 9, 0, 0, 0, . . . } 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 15

DELAY PROPERTY 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 16

GENERAL I/O PROBLEM § Input is x[n], find y[n] (for FIR, h[n]) § How to combine X(z) and H(z) ? 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 17

FIR Filter = CONVOLUTION 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 18 CONVOLUTION

CONVOLUTION PROPERTY § PROOF: MULTIPLY Z-TRANSFORMS 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 19

CONVOLUTION EXAMPLE § MULTIPLY the z-TRANSFORMS: MULTIPLY H(z)X(z) 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 20

CONVOLUTION EXAMPLE § Finite-Length input x[n] § FIR Filter (L=4) MULTIPLY Z-TRANSFORMS y[n] = ? 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 21

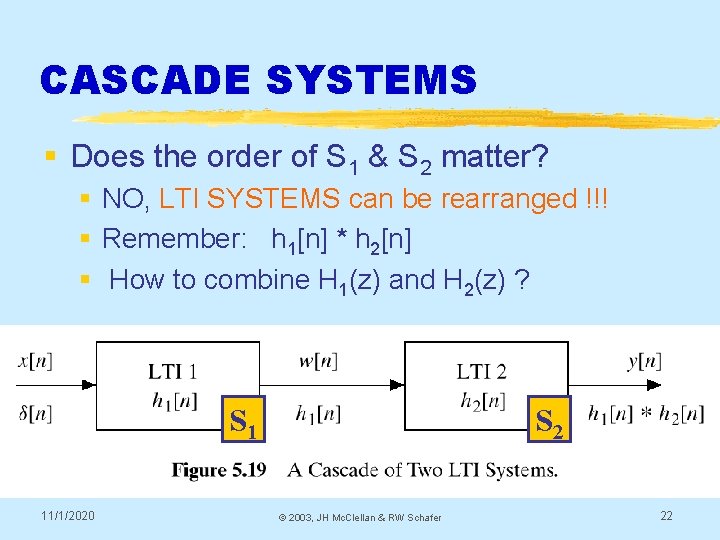
CASCADE SYSTEMS § Does the order of S 1 & S 2 matter? § NO, LTI SYSTEMS can be rearranged !!! § Remember: h 1[n] * h 2[n] § How to combine H 1(z) and H 2(z) ? S 1 11/1/2020 S 2 © 2003, JH Mc. Clellan & RW Schafer 22

CASCADE EQUIVALENT § Multiply the System Functions x[n] y[n] EQUIVALENT SYSTEM 11/1/2020 © 2003, JH Mc. Clellan & RW Schafer 23

CASCADE EXAMPLE x[n] w[n] x[n] 11/1/2020 y[n] © 2003, JH Mc. Clellan & RW Schafer 24