Signal Flow Graph nodes variables branches gains e

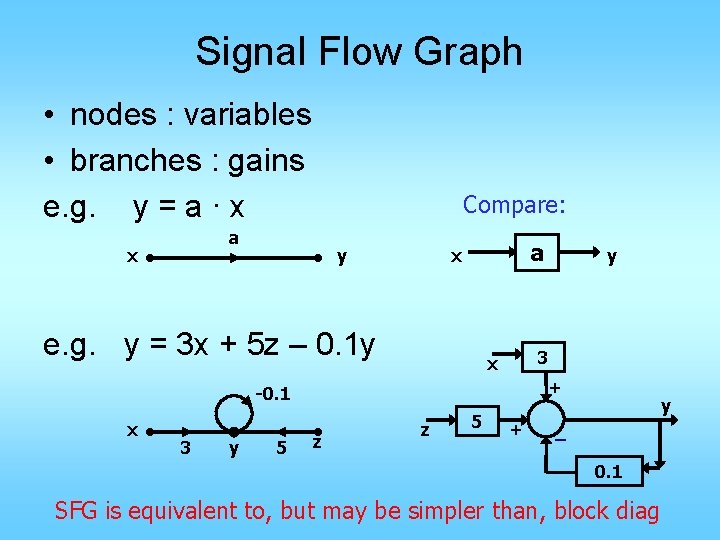
Signal Flow Graph • nodes : variables • branches : gains e. g. y = a ∙ x Compare: a x y a x e. g. y = 3 x + 5 z – 0. 1 y 3 x + -0. 1 x 3 y 5 y z z 5 + y – 0. 1 SFG is equivalent to, but may be simpler than, block diag

The value of a node is equal to the sum of all signals coming into the node. The incoming signals need to be weighted by the branch gains.

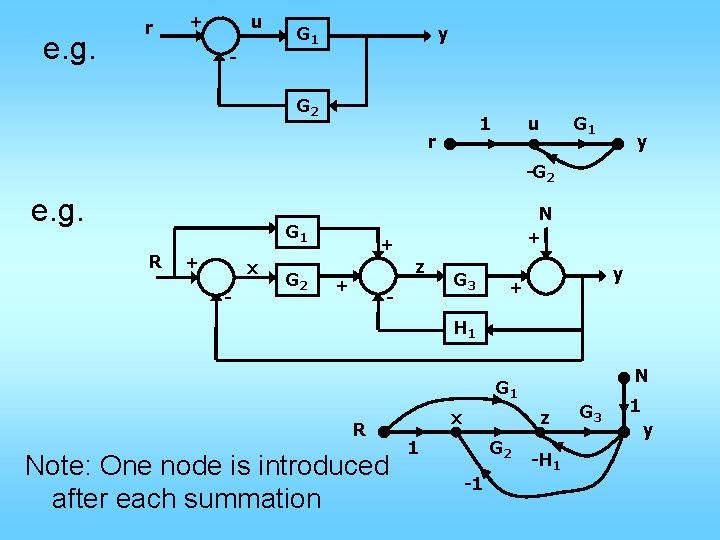
e. g. r + u - G 1 y G 2 1 r u G 1 y -G 2 e. g. G 1 R + x - G 2 N + + z + - G 3 y + H 1 N G 1 R Note: One node is introduced after each summation x z 1 G 2 -1 -H 1 G 3 1 y

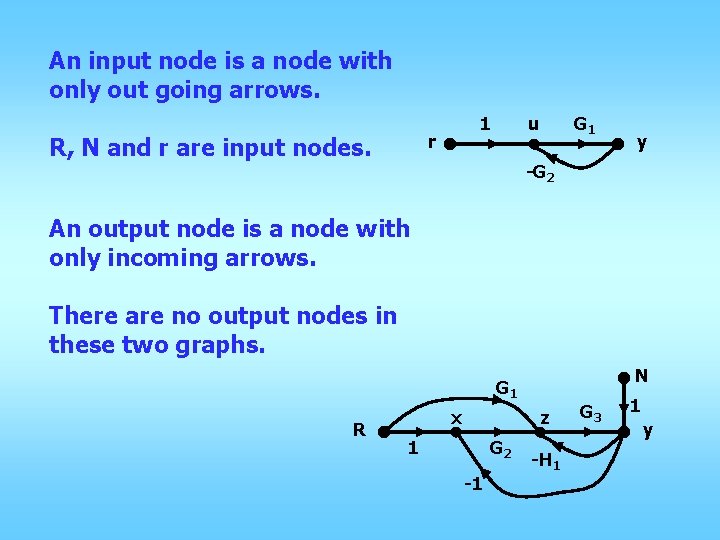
An input node is a node with only out going arrows. 1 r R, N and r are input nodes. u G 1 y -G 2 An output node is a node with only incoming arrows. There are no output nodes in these two graphs. N G 1 R x z 1 G 2 -1 -H 1 G 3 1 y

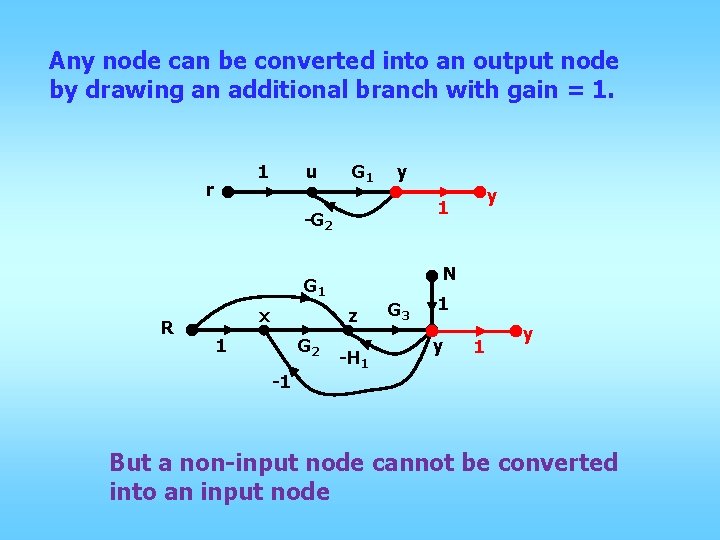
Any node can be converted into an output node by drawing an additional branch with gain = 1. 1 r u G 1 y -G 2 N G 1 R x z 1 G 2 -1 y 1 -H 1 G 3 1 y But a non-input node cannot be converted into an input node

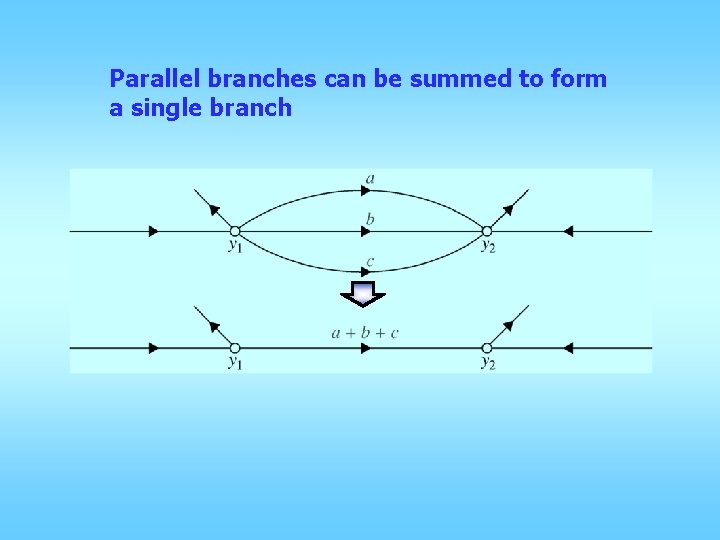
Parallel branches can be summed to form a single branch

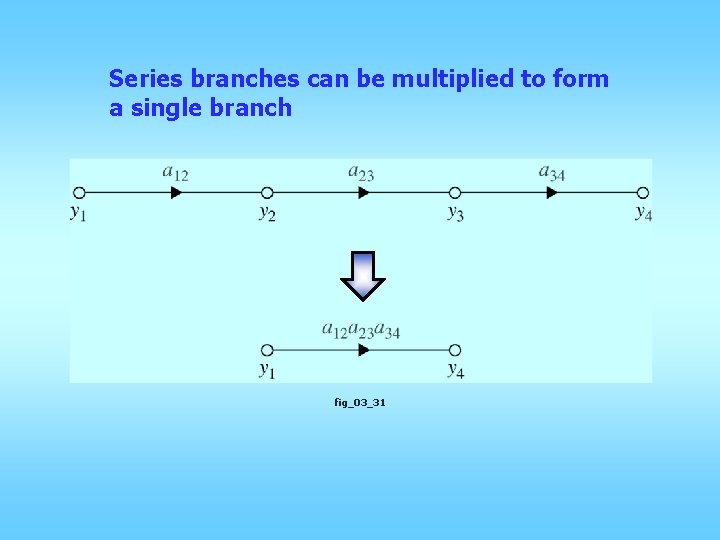
Series branches can be multiplied to form a single branch fig_03_31

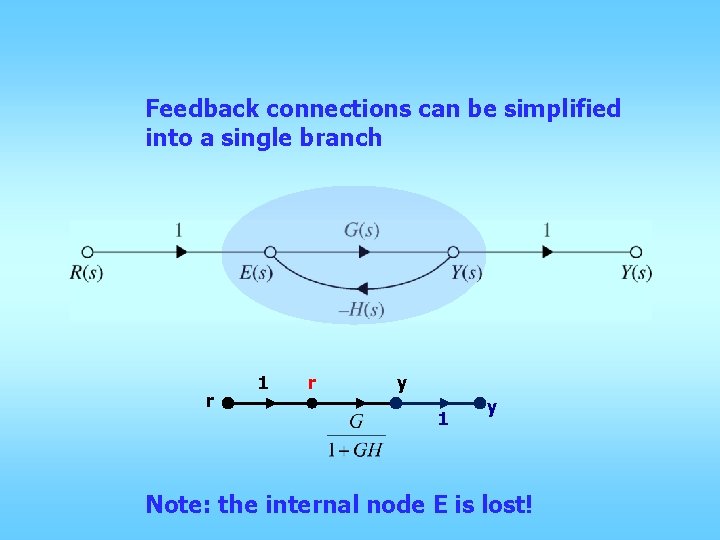
Feedback connections can be simplified into a single branch r 1 r y 1 y Note: the internal node E is lost!

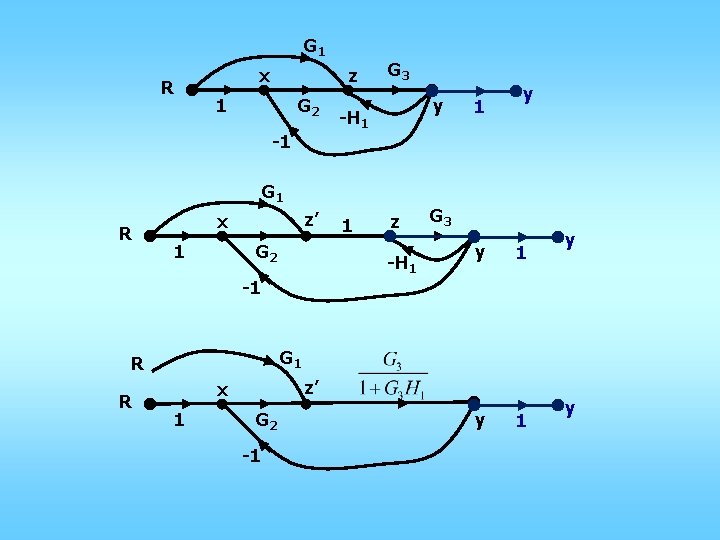
G 1 R x z 1 G 2 -1 G 3 y -H 1 G 1 R z’ x 1 G 2 z -H 1 -1 G 3 y 1 y G 1 R R 1 1 y z’ x 1 G 2 -1 y

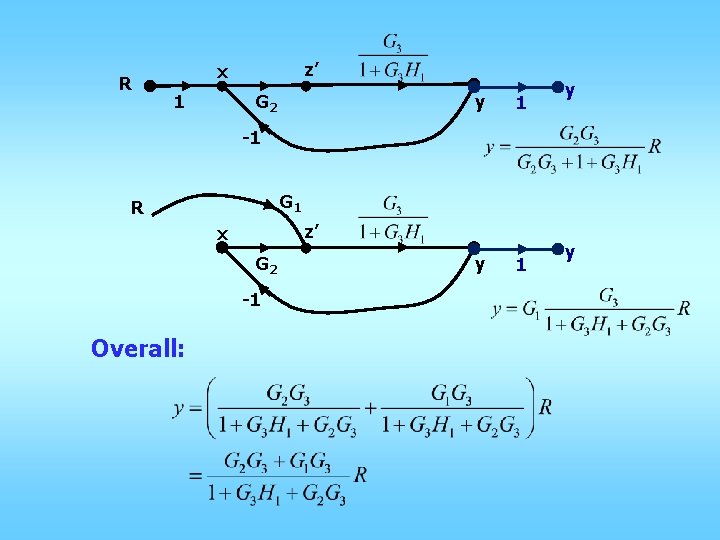
R z’ x 1 G 2 y 1 y -1 G 1 R z’ x G 2 -1 Overall: y

Mason’s Rule • A forward path: a path from input to output • Forward path gain Mk: total product of gains along the path • A loop is a closed path in which you can start at any point, follow the arrows, and come back to the same point • A loop gain Li: total product of gains along a loop • Loop i and loop j are non-touching if they do not share any nodes or branches

• The determinant Δ of a graph: • Δk: The determinant of the S. F. G. after removing the k-th forward path • Mason’s Rule:

e. g. G 1 R + x - G 2 N + + z + - G 3 y + H 1 N G 1 x R z 1 G 2 -1 -H 1 G 3 1 y

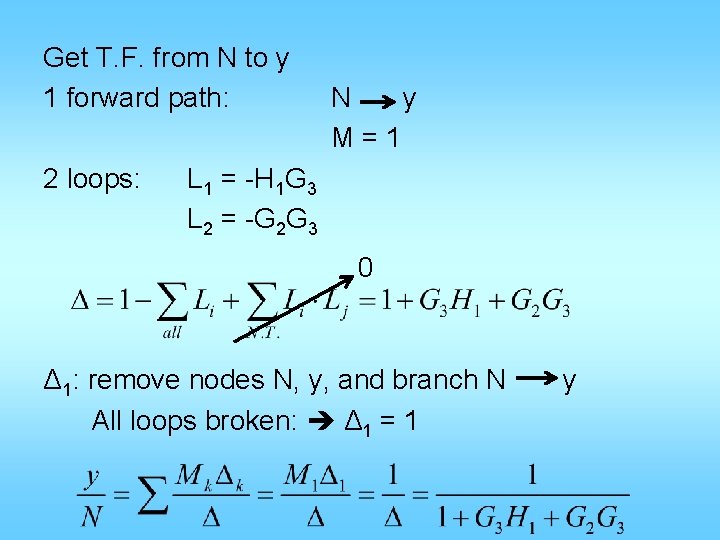
Get T. F. from N to y 1 forward path: 2 loops: N y M=1 L 1 = -H 1 G 3 L 2 = -G 2 G 3 0 Δ 1: remove nodes N, y, and branch N All loops broken: Δ 1 = 1 y

Get T. F. from R to y 2 f. p. : R x z R z y : 2 loops: L 1 = -G 3 H 1 L 2 = -G 2 G 3 0 y : M 1=G 2 G 3 M 2=G 1 G 3

Δ 1: remove M 1 and compute Δ Δ 1 = 1 Δ 2: remove M 2 and compute Δ Δ 2 = 1 Overall: Both denominators are the same, = D of overall graph. Only need to compute once, regardless # forward branches.

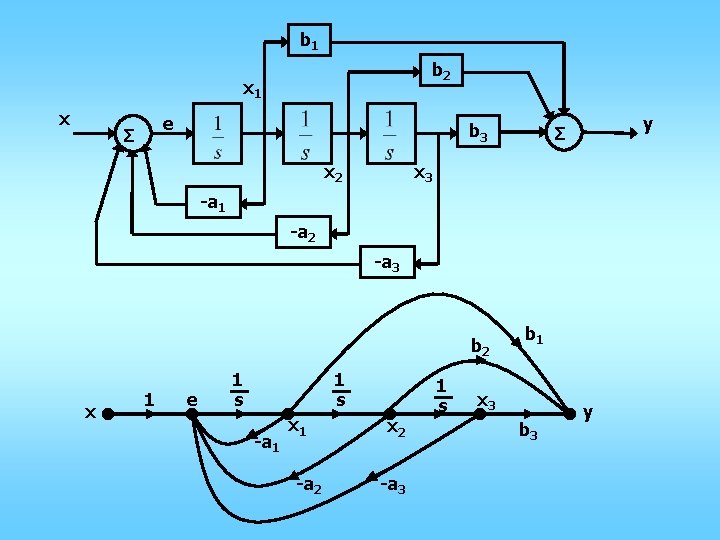
b 1 b 2 x 1 x e Σ b 3 x 2 y Σ x 3 -a 1 -a 2 -a 3 b 2 x 1 e 1 s -a 1 x 1 -a 2 x 2 -a 3 1 s b 1 x 3 b 3 y

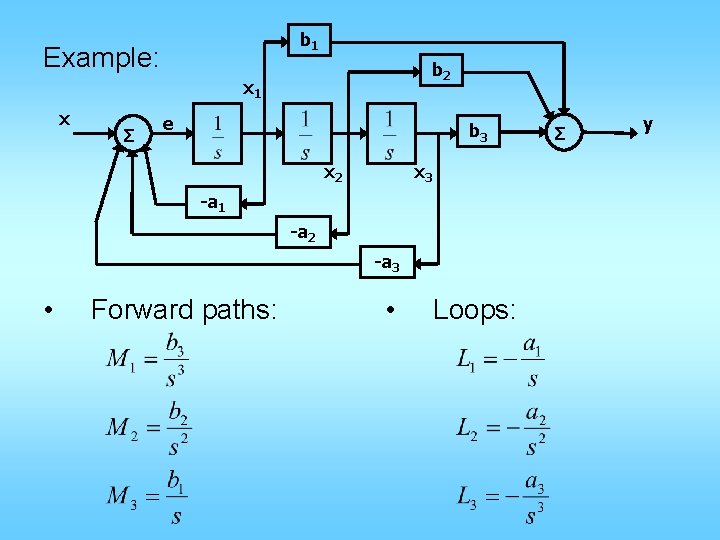
b 1 Example: b 2 x 1 x Σ e b 3 x 2 x 3 -a 1 -a 2 -a 3 • Forward paths: • Loops: Σ y

Determinant: Δ 1: If M 1 is taken out, all loops are broken. therefore Δ 1 = 1 Δ 2: If M 2 is taken out, all loops are broken. therefore Δ 2 = 1 Δ 3: Similarly, Δ 3 = 1

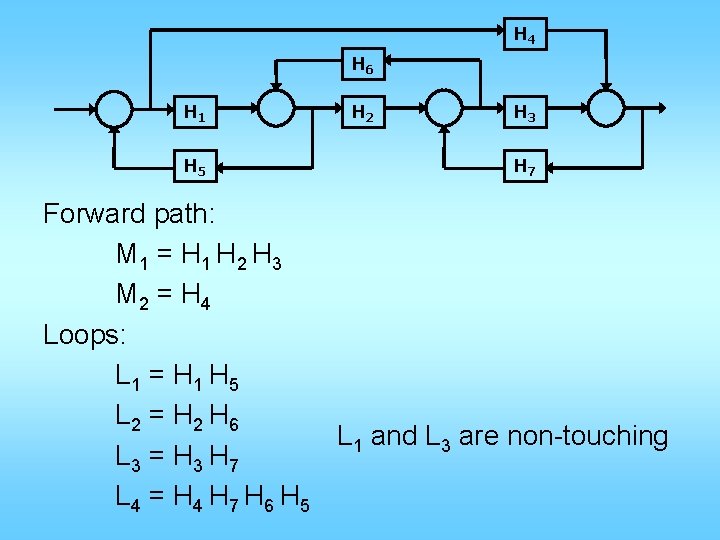
H 4 H 6 H 1 H 5 H 2 H 3 H 7 Forward path: M 1 = H 1 H 2 H 3 M 2 = H 4 Loops: L 1 = H 1 H 5 L 2 = H 2 H 6 L 1 and L 3 are non-touching L 3 = H 3 H 7 L 4 = H 4 H 7 H 6 H 5

Δ 1: If M 1 is taken out, all loops are broken. therefore Δ 1 = 1 Δ 2: If M 2 is taken out, the loop in the middle (L 2) is still therefore Δ 2 = 1 – L 2 = 1 – H 2 H 6 Total T. F. :

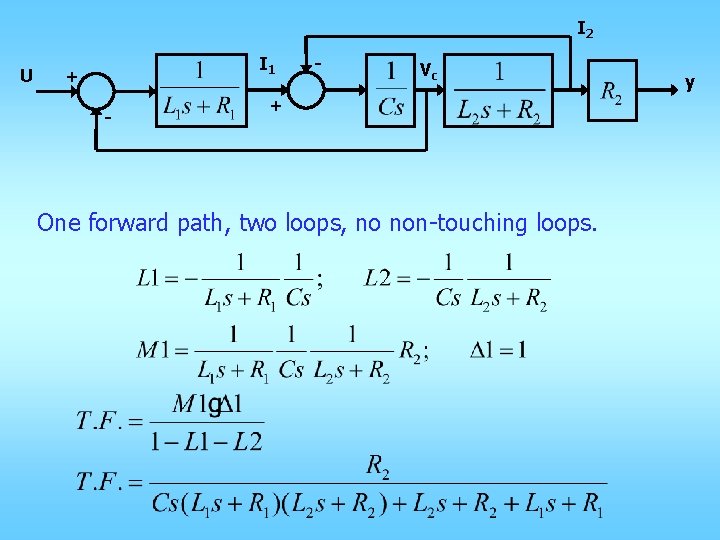
I 2 U I 1 + - - Vc + One forward path, two loops, no non-touching loops. y

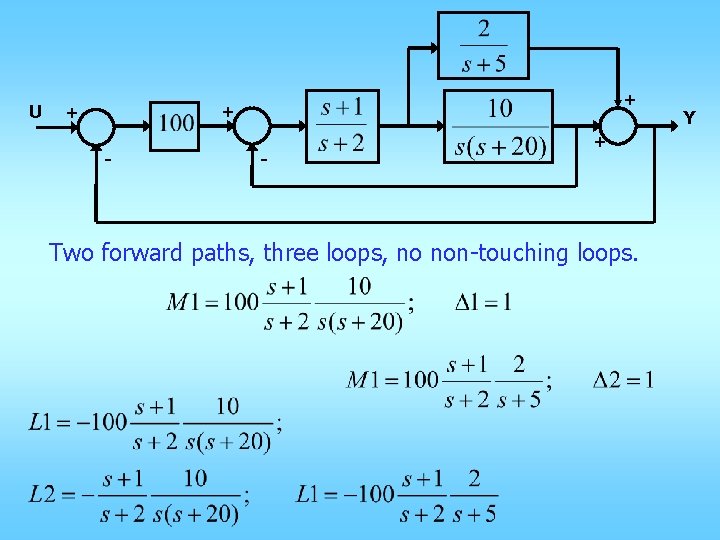
U + + + - - + Two forward paths, three loops, no non-touching loops. Y

Application to circuits • Identify input and output variables • At each internal “circuit node”: – Identify total impedance Z seen at this circuit node – Use current into this circuit node as a node variable – Use voltage at circuit node as another node variable – Gain from I to V is Z • Construct SFG for the circuit • Use Mason’s gain formula to find I/O TF