SIGMETRICSPerformance 2016 Generalized ThresholdBased Epidemics in Random Graphs

SIGMETRICS/Performance 2016 Generalized Threshold-Based Epidemics in Random Graphs: the Power of Extreme Values Michele Garetto, Università di Torino, Italy Emilio Leonardi, Politecnico di Torino, Italy Giovanni-Luca Torrisi, IAC-CNR, Rome, Italy

Outline Intro: bootstrap percolation n Prior work n Our contributions n Some details and insights n Conclusions and future work n 2

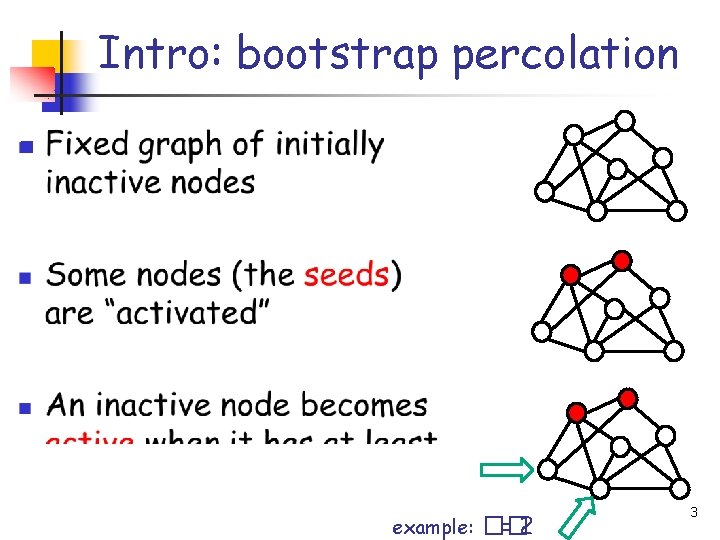
Intro: bootstrap percolation n example: �� =2 3

Prior work on bootstrap percolation n n historically, bootstrap percolation was first studied on regular graphs (grids, lattices, trees) In the last few years, bootstrap percolation has been analyzed also on random graphs S. Janson, T. Luczak, T. Turova, T. Vallier, “Bootstrap percolation on the random graph G(n, p)” The Annals of Applied Probability, 22(5), 2012 4

Bootstrap percolation on G(n, p) n 5

An idea of the approach n 6

An idea of the approach We obtain: n n For this process, consider the (asymptotic) trajectory of the mean 7

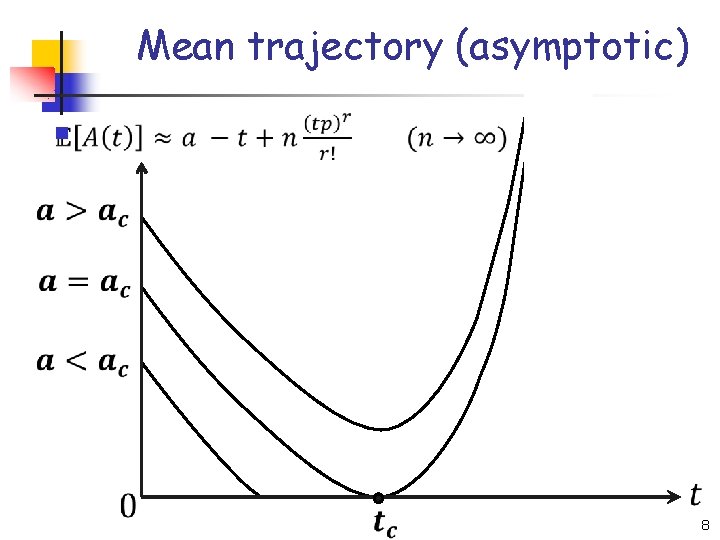
Mean trajectory (asymptotic) n 8

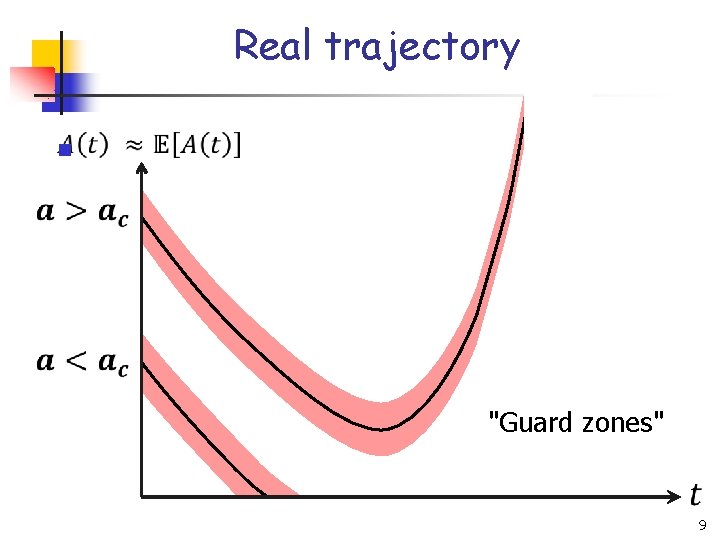
Real trajectory n "Guard zones" 9

Summary of contributions n 10

The role of extreme values n “Generalized Threshold-Based Epidemics in Random Graphs: the Power of Extreme Values” 11

Extension (1) n 12

Extension (1) - Example The critical number of seeds is the same ! 13

Extension (1) - application n n Propagation of a viral video over an online social networks Users receive suggestions from their friends (with positive/negative/null influence) When cumulative influence exceeds a (node-specific) threshold, user decides to watch the video (and possibly send suggestions to friends) It is reasonable to assume that “active nodes stay active for ever” 14

Extension (2) n 15

Extension (2) n (log-log scale) degree, d 16

Extension (2): experiment n Do we observe similar phase transitions? (under the same epidemic process) 17

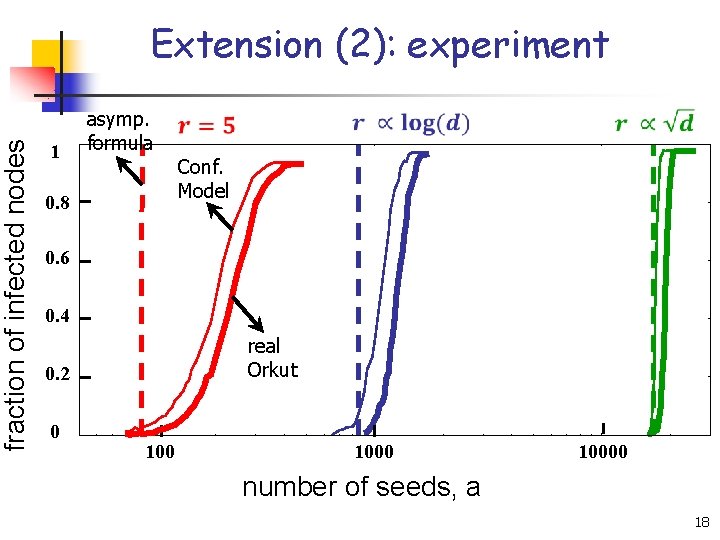
fraction of infected nodes Extension (2): experiment 1 asymp. formula Conf. Model 0. 8 0. 6 0. 4 real Orkut 0. 2 0 10000 number of seeds, a 18

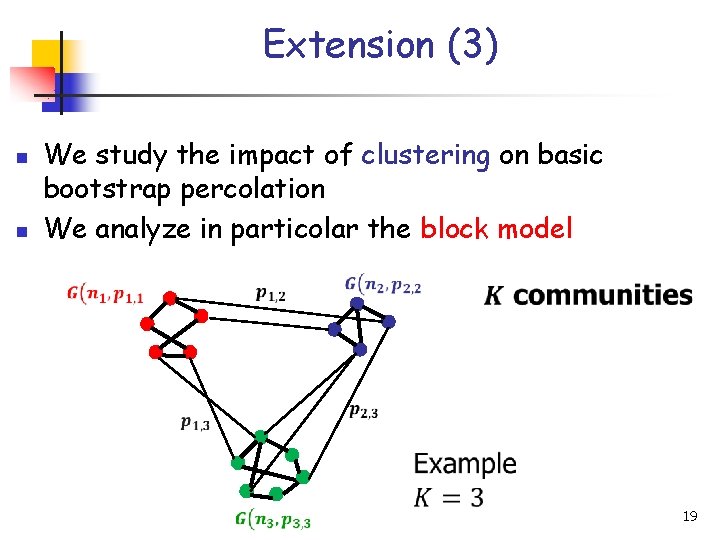
Extension (3) n n We study the impact of clustering on basic bootstrap percolation We analyze in particolar the block model 19

Extension (3) n For the block model, we obtain: n n n a formal proof of the fact that, to minimize the number of seeds, the optimal strategy is to put all of them in the same community (the most vulnerable community) sufficient (but not necessary) conditions on the number of seeds in each community leading to (almost) complete percolation of the whole graph an upper bound to the critical number of seeds in the entire system, assuming that seeds are selected uniformly at random among nodes A single (the most vulnerable) community can determine the phase transition of the whole system 20

Conclusions n 21

Thanks! 22