SIFAT DASAR ANALISIS REGRESI SIFAT DASAR REGRESI PENAFSIRAN

SIFAT DASAR ANALISIS REGRESI: SIFAT DASAR REGRESI, PENAFSIRAN MODEL REGRESI, REGRESI DAN PENYEBAB, REGRESI DAN Oleh : KORELASI Joko Prianto, SE. , MT. Disampaikan Pada Kuliah : Ekonometrika Terapan Jurusan Ekonomi Syariah FAI – UMM

PENGERTIAN KORELASI DAN REGRESI KORELASI dan REGRESI merupakan metode yang dapat digunakan untuk mengukur hubungan yang terjadi antar variabel-variabel ekonomi. Misal antara variabel X dan variabel Y. KORELASI T Korelasi mengukur derajat hubungan antara 2 atau lebih variabel. T Hubungan antara 2 Variabel (Misal X dan Y) dapat linear, non-linear, positif atau negatif.

Y . . . X . . . Y . Korelasi Linear: If semua titik (X, Y) pd diagram pencar mendekati bentuk garis lurus. Korelasi Non-linear: If semua titik (X, Y) pd diagram pencar tidak membentuk garis lurus. X . Y . . . Y X X Korelasi Positif: If jika arah perubahan kedua variabel sama If X naik, Y juga naik. Korelasi Negatif: If jika arah perubahan kedua variabel tidak sama If X naik, Y turun.

Koefisien korelasi ini memiliki nilai yang berkisar antara – 1 sampai 1. Bila yang diduga adalah koefisien korelasi sampel maka : rxy = sxy / sx. sy =

Pengujian Korelasi Meskipun mungkin telah diperoleh nilai koefisien korelasi dari hasil perhitungan di atas, namun keberartian nilai tersebut perlu di uji secara statistik. Hipotesis yang diuji adalah : Ho : Koefisien korelasi adalah sama dengan nol Ha : Koefisien korelasi tidak sama dengan nol, atau berarti

Pengujian koefisien ini dilakukan dengan uji-t, sehingga : . . . dengan derajat bebas = n – 2 Kriteria pengujiannya : Ho ditolak jika nilai t-hitung lebih besar daripada t-tabel dengan derajat bebas n-2, dan demikian pula sebaliknya.

Beberapa catatan tentang nilai r (korelasi): @ Secara empiris, hampir tidak pernah ditemukan korelasi sempurna (semua titik terpencar tepat pada garis). @ Nilai r yang mendekati nol menunjukkan derajat hubungan yang lemah. @ Koefisien r merupakan estimasi sampel terhadap koefisien korelasi populasi, . @ Nilai r mengandung error, sehingga perlu diuji reliabilitasnya.

Konsep dasar Ekonometrika merupakan suatu ilmu tersendiri yang merupakan penggabungan dari teori ekonomi, statistik dan matematik, dalam upaya untuk menggambarkan suatu fenomena. Langkah I: Kajian teori ekonomi dan penelitian terdahulu Langkah II: Formulasi model atau spesifikasi model Langkah III: Merancang metode dan prosedur untuk mendapatkan sampel representatif Langkah IV: Estimasi model No Langkah V: Menguji hipotesis/ verifikasi menggunakan statistik inferensi (Uji-t, Uji-F, dll) Yes Langkah VII: Interpretasi hasil Langkah VIII: Kesimpulan

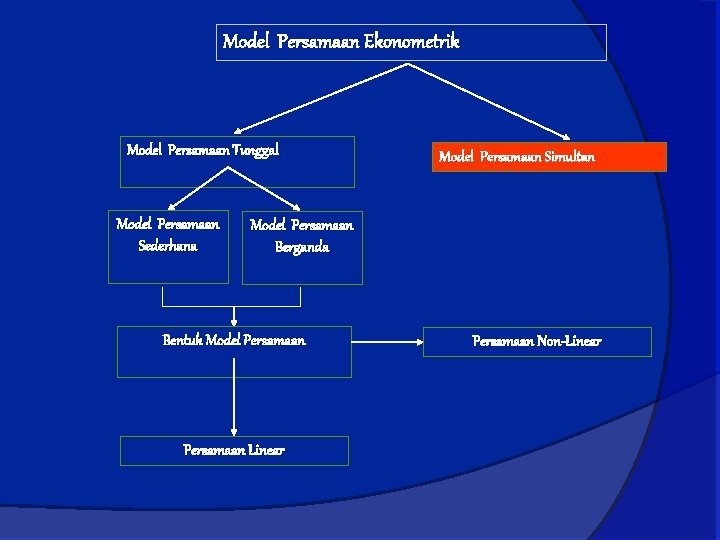
Model Persamaan Ekonometrik Model Persamaan Tunggal Model Persamaan Sederhana Model Persamaan Simultan Model Persamaan Berganda Bentuk Model Persamaan Linear Persamaan Non-Linear

Model Regresi Sederhana Yi = 0 + 1 Xi + i 2 0 dan 1 : parameter dari fungsi yg nilainya akan diestimasi. 2 Bersifat stochastik untuk setiap nilai X terdapat suatu distribusi probabilitas seluruh nilai Y atau Nilai Y tidak dapat diprediksi secara pasti karena ada faktor stochastik i yang memberikan sifat acak pada Y. 2 Adanaya variabel i disababkan karena: Ketidak-lengkapan teori Perilaku manusia yang bersifat random Ketidak-sempurnaan spesifikasi model Kesalahan dalam agregasi Kesalahan dalam pengukuran

Y . i . 0 . Y. i Ÿi = b 0 + b 1 Xi . Ÿi . . Yi . Variation in Y X = 0 + 1 Xi + Systematic Variation i Random Variation

Asumsi-asumsi mengenai I (Variabel pengganggu) 1. i adalah variabel random yg menyebar normal 2. Nilai rata-rata i = 0, e( i) = 0. 3. Tidak tdpt serial korelasi antar i cov( i, j) = 0 4. Sifat homoskedastistas, var( i) = 2 5. cov( i, Xi) = 0 6. Tidak terdapat bias dalam spesifikasi model 7. Tidak terdapat multi-collinearity antar variebel penjelas

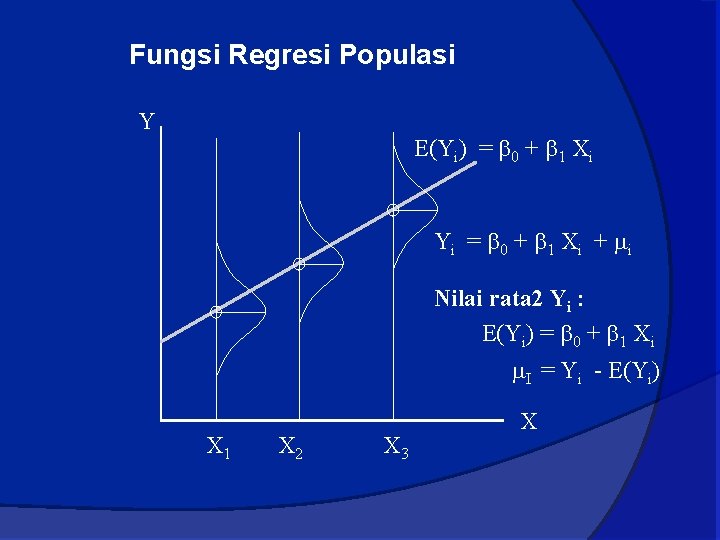
Fungsi Regresi Populasi Y E(Yi) = 0 + 1 Xi Yi = 0 + 1 Xi + i Nilai rata 2 Yi : E(Yi) = 0 + 1 Xi I = Yi - E(Yi) X 1 X 2 X 3 X

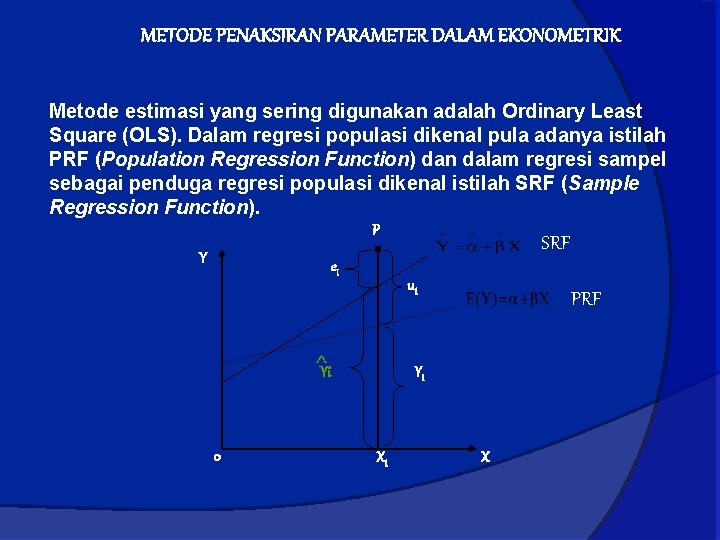
METODE PENAKSIRAN PARAMETER DALAM EKONOMETRIK Metode estimasi yang sering digunakan adalah Ordinary Least Square (OLS). Dalam regresi populasi dikenal pula adanya istilah PRF (Population Regression Function) dan dalam regresi sampel sebagai penduga regresi populasi dikenal istilah SRF (Sample Regression Function). P Y ei ui ^Yi 0 SRF PRF Yi Xi X

Penaksir kuadrat terkecil adalah mempunyai varian yang minimum yaitu penaksir tadi bersifat BLUE (Best Linear Unbiased Estimator). Asumsi yang harus dipenuhi dalam penaksiran metode OLS adalah sebagai berikut : 1. i adalah sebuah variabel acak atau random yang riil dan memiliki distribusi normal. 2. Nilai harapan dari i yang timbul karena variasi nilai Xi yang diketahui harus sama dengan nol. E( i/ Xi) = 0 3. Tidak terjadi autokorelasi atau serial korelasi. Artinya, Cov( i, j) = E i – E( i) j – E( j) = E( i, j) = 0. . . . . i j 4. Syarat Homoskedastisiti. Artinya bahwa varian dari i adalah konstan dan sama dengan 2. Var ( i / Xi) = E i – E( i) 2 = E( i)2 = 2 5. Tidak terjadi multikolonieritas. Yaitu tidak ada korelasi antara dengan variabel bebasnya Xi atau : Cov( i , Xi) = E( i – E( i))(Xi – E(Xi)) = 0

REGRESI LINEAR SEDERHANA Y = ß 0 + ß 1 X Pengujian statistik SECARA PARSIAL mendasarkan pada hipotesis : Uji Konstanta Intersep H 0 Uji Koeff. X : H 1 : ß 0 = 0 ß 0 ≠ 0 : ß 1 = 0 H 1 : ß 1 ≠ 0 Pengujian statistik model secara keseluruhan dilakukan dengan uji. F. Uji F mendasarkan pada dua hipotesis, yaitu : H 0 H 1 H 0 : Semua koefisien variabel bebas adalah 0 (nol) : Tidak seperti tersebut di atas

Contoh : Sehingga dapat disajikan hasil sebagai berikut : S. E t-hitung = F hit = 202, 868 Df = 8 Konsumsi = 24. 455 + 0. 509*Income R 2 = 0. 962 (6. 414) (0. 036) 3. 813 14. 243 Dalam pengertian ekonomi dapat dikatakan bahwa jika terdapat kenaikan income sebesar $ 1 per bulan maka akan mempengaruhi kenaikan pula pada konsumsi sebesar $ 0. 509. Demikian juga bila terjadi penurunan income sebesar $ 1 per bulan maka akan berdampak pada penurunan konsumsi sebesar $ 0. 509.

Estimasi Parameter Model Regresi Sederhana Y i = 0 + 1 X i + i Metode Kuadrat Terkecil (Ordinary Least Square – OLS): Prinsip: Meminimumkan nilai error – mencari jumlah penyimpangan kuadrat ( i 2) terkecil. i = Y i - 0 - 1 X i i 2 = (Yi - 0 - 1 Xi)2 i 2 = (Yi - 0 - 1 Xi)2 i 2 minimum jika: i 2 / 0 = 0 2 (Yi - 0 - 1 Xi) = 0 i 2 / 1 = 0 2 Xi (Yi - 0 - 1 Xi) = 0

Sederhanakan, maka didapat: (Xi – X) (Yi – Y) b 1 = (Xi – X)2 b 0 = Y - b 1 X dimana b 0 dan b 1 nilai penduga untuk 0 dan 1. X dan Y adlh nilai rata 2 pengamatan X dan Y Standar error: 2 ½ SE(b 1) = SE(b 0) = (Xi – X)2 X i 2 N (Xi – diduga dengan s, dimana: s = ( i 2 /n-2)2 dan i 2 = (Yi – Y)2 X)2 ½

Metode Ordinary Least Squares (OLS) Yi = 1 + 2 Xi + i(1) Yi = 1 + 2 Xi + i (2) Ŷi = 1 + 2 X i (3) Y i = Ŷ i + i (4) i = Y i - Ŷ i (5) 2 = = = n Xi. Yi – Xi Yi n Xi 2 – ( Xi)2 (Xi – X)(Yi – Y) (Xi – X)2 n xiyi xi 2 Persamaan umum Regresi sederhana 1 dan 2 adalah nilai estimasi untuk parameter Ŷi = nilai estimasi model i = nilai residual 1 = (Xi )2 Yi – Xi Xi. Yi n Xi 2 – ( Xi)2 = Y – 2 X Koefisien parameter untuk 1 dan 2

Standard error of the estimates Var( 2) = 2 / Xi 2 Se( 2) = Var( 1) = Var( 2) = Xi 2 n xi 2 Se( 1) = 2 = i 2 n– 2 2 Xi 2 = Xi 2 2 Var( 1) = Xi 2 n xi 2 2 i 2 = yi 2 – 22 xi 2 = yi 2 – (xi yi) 2 xi 2

Koefisien Determinasi • Y TSS Y 1 + 2 Xi RSS TSS = RSS + ESS 1= X r 2 = ESS TSS atau = 1– = ESS TSS = (Ŷi - Y)2 (Yi = 1– ESS TSS (Yi - Y)2 r 2 = 22 i 2 Y)2 TSS (Ŷi - Y)2 Atau: Y)2 (Yi - + RSS = + i 2 (Yi - Y)2 xi 2 yi 2 (xi yi) 2 xi 2 yi 2

TERIMA KASIH