SIF1033 Traitement dimage u Sujets Dtection des contours

SIF-1033 Traitement d’image u Sujets – Détection des contours et arêtes – Dérivée première (gradient) – Dérivée seconde * Laplacien de la gaussienne – Détection de contour (python) – Filtre de Canny (python) u Lectures: Notes de cours

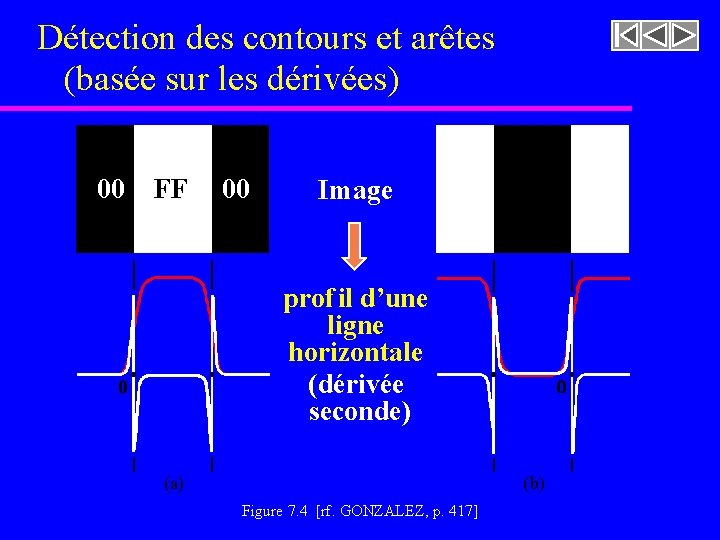
Détection des contours et arêtes (basée sur les dérivées) 00 FF 00 Image prof il d’une ligne horizontale (dérivée première) seconde) ( b) (a) Figure 7. 4 [rf. GONZALEZ, p. 417]

Dérivée première (gradient) | Gx | + | Gy | -1 -2 0 -1 1 0 0 02 | Gyx | -2 1 20 1 -1 Figure 7. 6 [rf. GONZALEZ, p. 421]

Dérivée seconde (Laplacien) u Le calcul du laplacien découle de la forme suivante: u La forme digitale est donnée par: 0 -1 4 -1 0 z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 • Cette méthode est sensible au bruit

Dérivée seconde (Laplacien) u Le laplacien de la gaussienne permet de corriger les problèmes de sensibilité au bruit de la méthode du laplacien u Le laplacien de la gaussienne prend la forme:

Dérivée seconde (Laplacien) u Nous utilisons la forme:

Dérivée seconde (Laplacien de la gaussienne) Figure 7. 8 [rf. GONZALEZ, p. 423]

Dérivée seconde (Laplacien) u Le résultat de la convolution f *g’’ est la dérivée seconde de l’image u Il faut alors localiser les passages par zéro de la dérivée de l’image pour permettre la localisation des contours dans l’image u Pour localiser les passages par zéros nous utilisons une petite fenêtre de 1 X 2 pour localiser les passages par zéros verticaux et une de 2 X 1 pour ceux horizontaux

Dérivée seconde (Laplacien) u Par la suite nous parcourons l’image des dérivées secondes et effectuons les tests suivants: i j j+1 SI ((((f*g’’)(i, j) > 0) ET ((f*g’’)(i, j+1) < 0)) OU (((f*g’’)(i, j) < 0) ET ((f*g’’)(i, j+1) > 0))) ALORS Passage par zéro (contour vertical) j i i+1 SI ((((f*g’’)(i, j) > 0) ET ((f*g’’)(i+1, j) < 0)) OU (((f*g’’)(i, j) < 0) ET ((f*g’’)(i+1, j) > 0))) ALORS Passage par zéro (contour horizontal)

Laplacien de la gaussienne (exemples) Image originale (320 X 320 pixels) Convolution de l’image avec {Laplacien de G} où w 2 -D = 8 (valeurs positives en blanc (0 apparaissant en gris) (montre seulement les passages par 0 en noir) et négatives en noir) Figure 2 -12 [rf. MARR, p. 58]

Exemple de détection de contours /u/dmatensr/meunier/images/riviere. rast

Détection de contours (python)

Détection de contours (python)

Détection de contours (python)

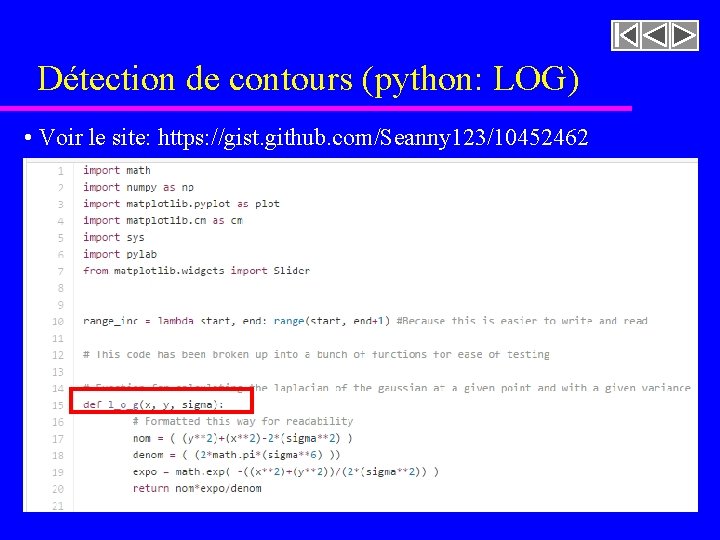
Détection de contours (python: LOG) • Voir le site: https: //gist. github. com/Seanny 123/10452462

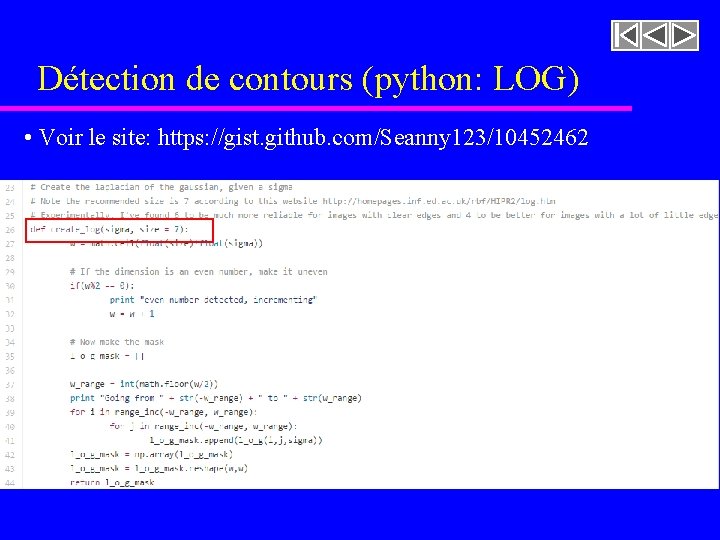
Détection de contours (python: LOG) • Voir le site: https: //gist. github. com/Seanny 123/10452462

Détection de contours (python: LOG) • Voir le site: https: //gist. github. com/Seanny 123/10452462

Détection de contours (python: LOG) • Voir le site: https: //gist. github. com/Seanny 123/10452462

Détection de contours (python: LOG) • Voir le site: https: //gist. github. com/Seanny 123/10452462

Filtre de Canny u Étape 1: Calcul des dérivées Horizontale et Verticale d I(x, y)/dx d I(x, y)/dy

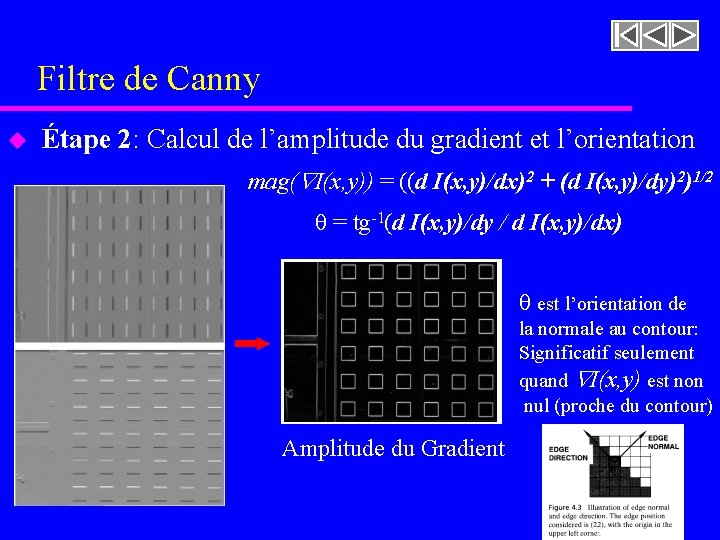
Filtre de Canny u Étape 2: Calcul de l’amplitude du gradient et l’orientation mag( I(x, y)) = ((d I(x, y)/dx)2 + (d I(x, y)/dy)2)1/2 = tg-1(d I(x, y)/dy / d I(x, y)/dx) est l’orientation de la normale au contour: Significatif seulement quand I(x, y) est non nul (proche du contour) Amplitude du Gradient

Filtre de Canny u Étape 3: Éliminer les pixels ne correspondant pas à des maximas: – Un pixel a une réponse maximale si ces deux voisins selon l’axe de la normale ont une réponse inférieure • Les pixel non-max sont mis à 0 u Étape 4: Seuillage par hystérésis – a) Si mag( I(x, y)) > Seuil 1 1 pixel de contour – b) Suivre le contour TTQ mag( I(x, y)) > Seuil 2 – Produit des contours assez continus – Seuil 1 est souvent fixé à 2 * Seuil 2

Filtre de Canny u Exemple d’utilisation du filtre de Canny (Utilisation de la fonction cv. Canny() dans Open. CV)

Filtre de Canny u Exemple: edge. c dans le dossier C: Program FilesOpen. CVsamplesc de Open. CV Seuil 1 Seuil 2 Dim Sobel

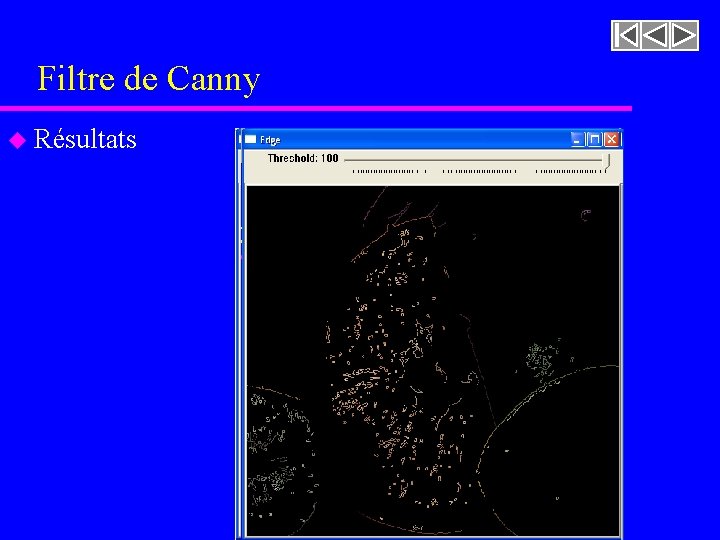
Filtre de Canny u Résultats

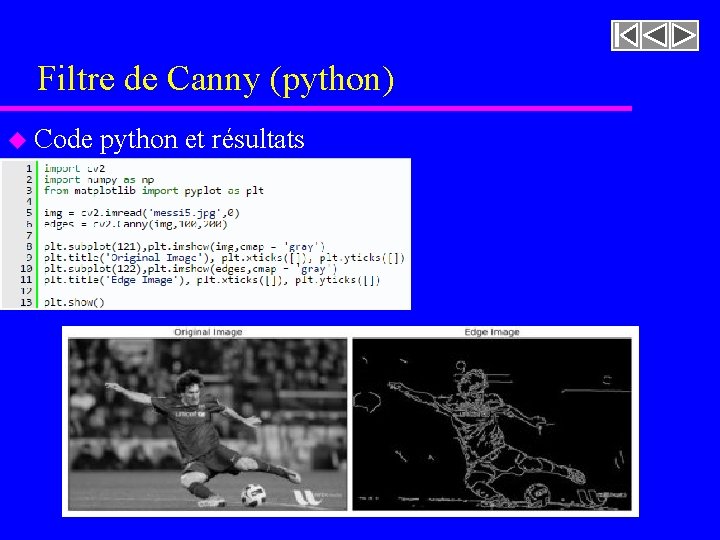
Filtre de Canny (python) u Code python et résultats

Résumé u Segmentation des images par détection de contours et d’arêtes – Dérivée première (gradient) – Dérivée seconde * Laplacien de la gaussienne – Détection de contour (python) – Filtre de Canny (python)