ShuntSeries Feedback Amplifier Ideal Case Current feedback Current

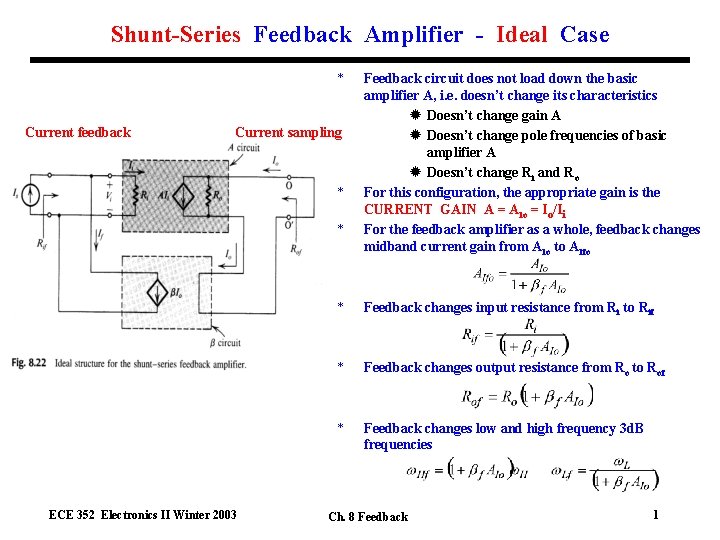
Shunt-Series Feedback Amplifier - Ideal Case * Current feedback Current sampling * * ECE 352 Electronics II Winter 2003 Feedback circuit does not load down the basic amplifier A, i. e. doesn’t change its characteristics ® Doesn’t change gain A ® Doesn’t change pole frequencies of basic amplifier A ® Doesn’t change Ri and Ro For this configuration, the appropriate gain is the CURRENT GAIN A = AIo = Io/Ii For the feedback amplifier as a whole, feedback changes midband current gain from AIo to AIfo * Feedback changes input resistance from Ri to Rif * Feedback changes output resistance from Ro to Rof * Feedback changes low and high frequency 3 d. B frequencies Ch. 8 Feedback 1

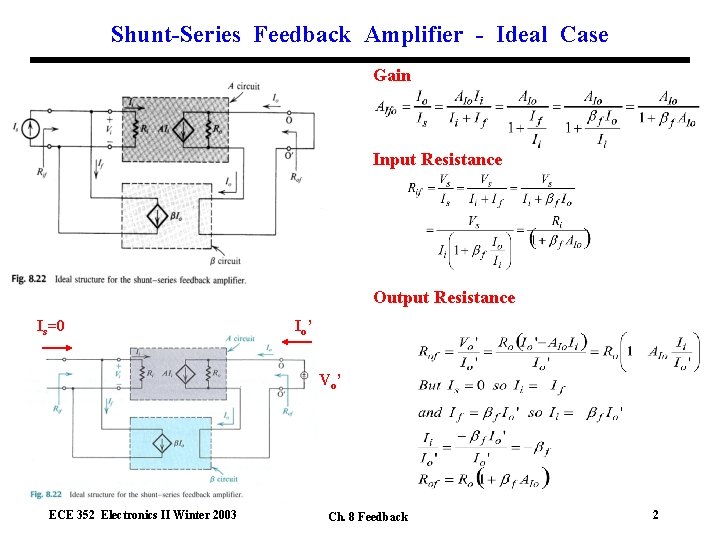
Shunt-Series Feedback Amplifier - Ideal Case Gain Input Resistance Output Resistance Is=0 Io’ Vo’ ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 2

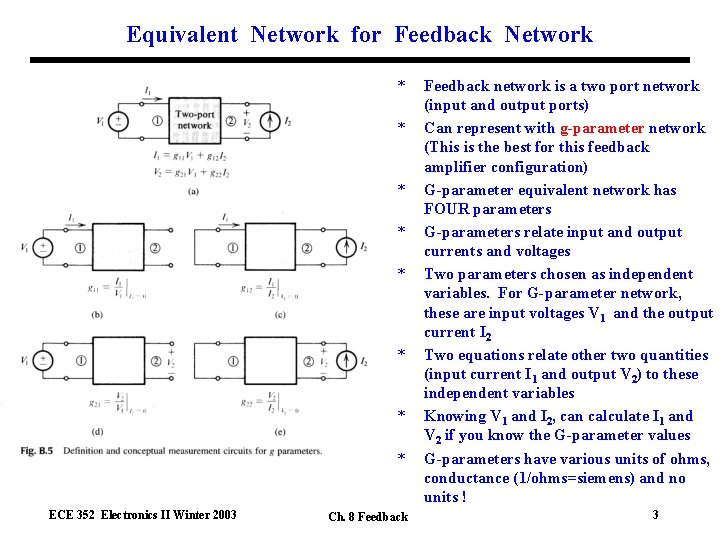
Equivalent Network for Feedback Network * * * * ECE 352 Electronics II Winter 2003 Ch. 8 Feedback network is a two port network (input and output ports) Can represent with g-parameter network (This is the best for this feedback amplifier configuration) G-parameter equivalent network has FOUR parameters G-parameters relate input and output currents and voltages Two parameters chosen as independent variables. For G-parameter network, these are input voltages V 1 and the output current I 2 Two equations relate other two quantities (input current I 1 and output V 2) to these independent variables Knowing V 1 and I 2, can calculate I 1 and V 2 if you know the G-parameter values G-parameters have various units of ohms, conductance (1/ohms=siemens) and no units ! 3

Shunt-Series Feedback Amplifier - Practical Case * * * Feedback network consists of a set of resistors These resistors have loading effects on the basic amplifier, i. e they change its characteristics, such as the gain Can use g-parameter equivalent circuit for feedback network æ Feedback factor f given by g 12 since Feedforward factor given by g 21 (neglected) æ g 22 gives feedback network loading on output æ g 11 gives feedback network loading on input Can incorporate loading effects in a modified basic amplifier. Gain AIo becomes a new, modified gain AIo’. Can then use analysis from ideal case æ I 2 I 1 g 22 * V 1 g 12 I 2 g 21 V 1 ECE 352 Electronics II Winter 2003 V 2 * Ch. 8 Feedback 4

Shunt-Series Feedback Amplifier - Practical Case * * * I 2 I 1 V 1 g 22 g 11 g 12 I 2 g 21 V 1 ECE 352 Electronics II Winter 2003 * V 2 Ch. 8 Feedback How do we determine the g-parameters for the feedback network? For the input loading term g 11 æ We turn off the feedback signal by setting Io = I 2 = 0. æ We then evaluate the resistance seen looking into port 1 of the feedback network. For the output loading term g 22 æ We short circuit the connection to the input so V 1 = 0. æ We find the resistance seen looking into port 2 of the feedback network. To obtain the feedback factor f (also called g 12 ) æ We apply a test signal Io’ to port 2 of the feedback network and evaluate the feedback current If (also called I 1 here) for V 1 = 0. æ Find f from f = If/Io’ 5

Example - Shunt-Series Feedback Amplifier * * * Two stage [CE+CE] amplifier Transistor parameters Given: =100, rx= 0 Input and output coupling and emitter bypass capacitors, but direct coupling between stages Capacitor in feedback connection removes Rf from DC bias of two stages is coupled (bias of one affects the other) ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 6

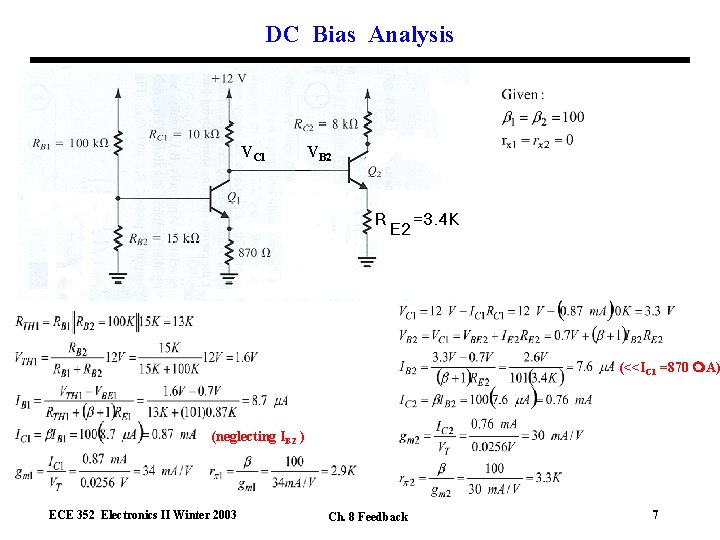
DC Bias Analysis VC 1 VB 2 (<<IC 1 =870 A) (neglecting IB 2 ) ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 7

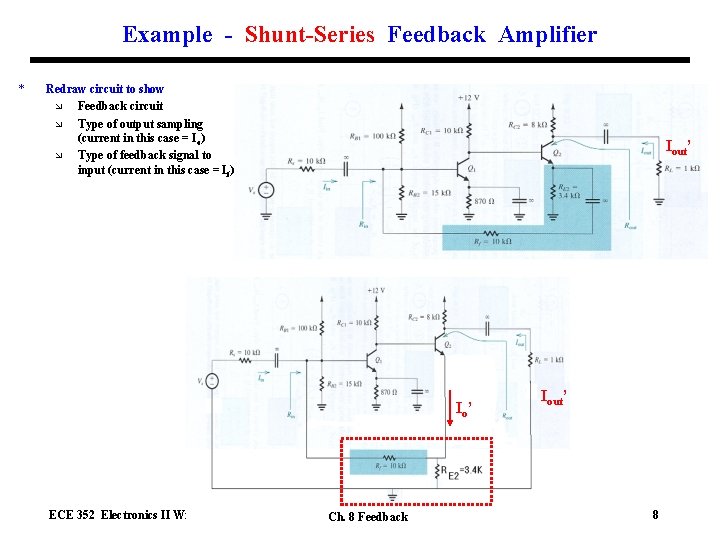
Example - Shunt-Series Feedback Amplifier * Redraw circuit to show æ Feedback circuit æ Type of output sampling (current in this case = Io) æ Type of feedback signal to input (current in this case = If) Iout’ Io’ ECE 352 Electronics II Winter 2003 Ch. 8 Feedback Iout’ 8

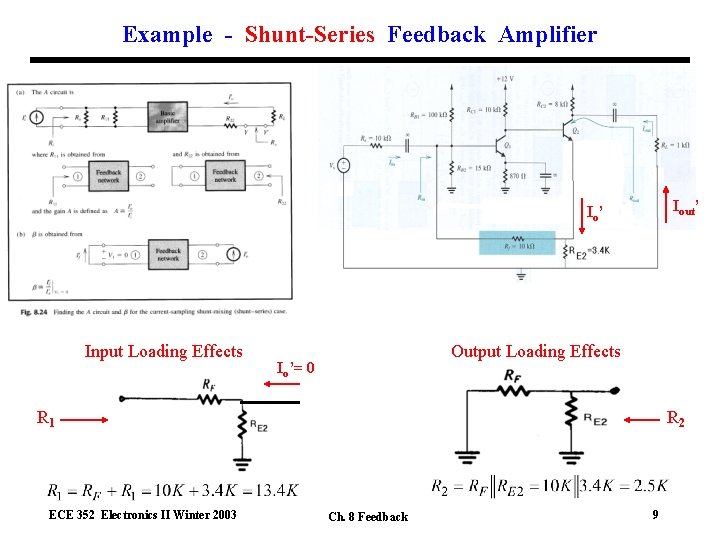
Example - Shunt-Series Feedback Amplifier Iout’ Io’ Input Loading Effects Output Loading Effects Io’= 0 R 1 ECE 352 Electronics II Winter 2003 R 2 Ch. 8 Feedback 9

Example - Shunt-Series Feedback Amplifier with Loading Effects but Without Feedback ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 10

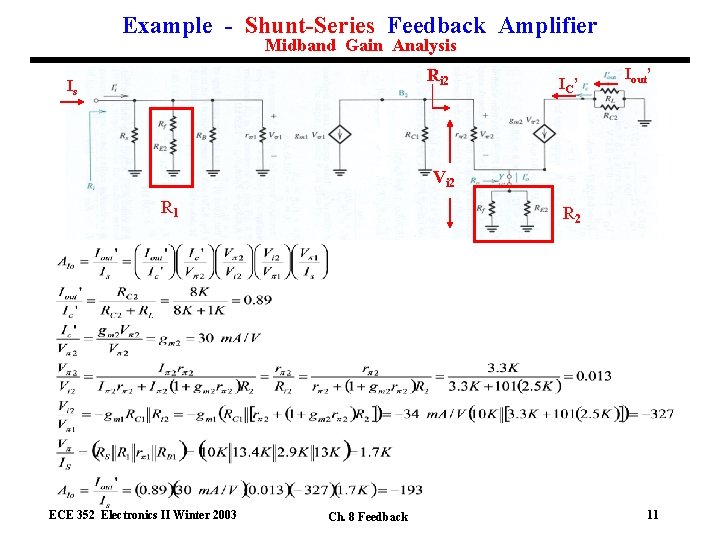
Example - Shunt-Series Feedback Amplifier Midband Gain Analysis Ri 2 Is I C’ Iout’ Vi 2 R 1 ECE 352 Electronics II Winter 2003 R 2 Ch. 8 Feedback 11

Midband Gain with Feedback * Determine the feedback factor f + VE 2 * Calculate gain with feedback AIfo * Note æ æ æ - f < 0 and AIo < 0 f AIo > 0 as necessary for negative feedback and dimensionless f AIo is large so there is significant feedback. Can change f and the amount of feedback by changing RF. Gain is determined by feedback resistance ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 12

Input and Output Resistances with Feedback Ro Ri * Determine input Ri and output Ro resistances with loading effects of feedback network. * Calculate input Rif and output Rof resistances for the complete feedback amplifier. ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 13

Voltage Gain for Current Gain Feedback Amplifier * Can calculate voltage gain * Note - can’t calculate the voltage gain as follows: ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 14

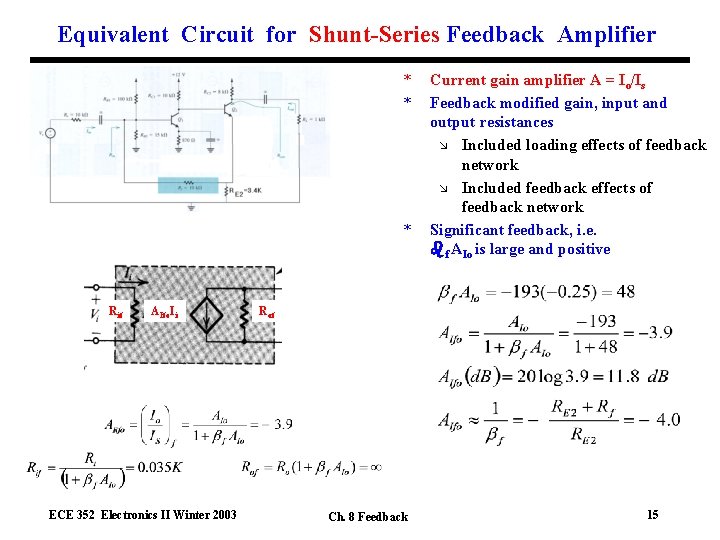
Equivalent Circuit for Shunt-Series Feedback Amplifier * * * Rif AIfo. I i ECE 352 Electronics II Winter 2003 Current gain amplifier A = Io/Is Feedback modified gain, input and output resistances æ Included loading effects of feedback network æ Included feedback effects of feedback network Significant feedback, i. e. f AIo is large and positive Rof Ch. 8 Feedback 15

Frequency Analysis * * * ECE 352 Electronics II Winter 2003 Ch. 8 Feedback Low frequency analysis of poles for feedback amplifier follows Gray-Searle (short circuit) technique as before. Low frequency zeroes found as before. Dominant pole used to find new low 3 d. B frequency. For high frequency poles and zeroes, substitute hybrid-pi model with C and C (transistor’s capacitors). æ Follow Gray-Searle (open circuit) technique to find poles High frequency zeroes found as before. Dominant pole used to find new high 3 d. B frequency. 16

Summary of Feedback Amplifier Analysis * Xs Xi Xo Xf f • Calculate low frequency poles and zeroes. • Determine dominant (highest) low frequency pole L including loading effects of feedback network • Calculate new dominant low frequency pole Lf. * • Calculate high frequency poles and zeroes. • Determine dominant (lowest) high frequency pole H including loading effects of feedback network • Calculate new dominant high frequency pole Hf. * * ECE 352 Electronics II Winter 2003 * Ch. 8 Feedback Identify the amplifier configuration by: æ Output sampling ® Io = series configuration ® Vo = shunt configuration æ Feedback to input ® Io = shunt configuration ® Vo = series configuration Calculate loading effects of feedback network æ On input æ On output Calculate appropriate midband gain A’ (modified by loading effects of feedback network) Calculate feedback factor f. Calculate midband gain with feedback Af. 17

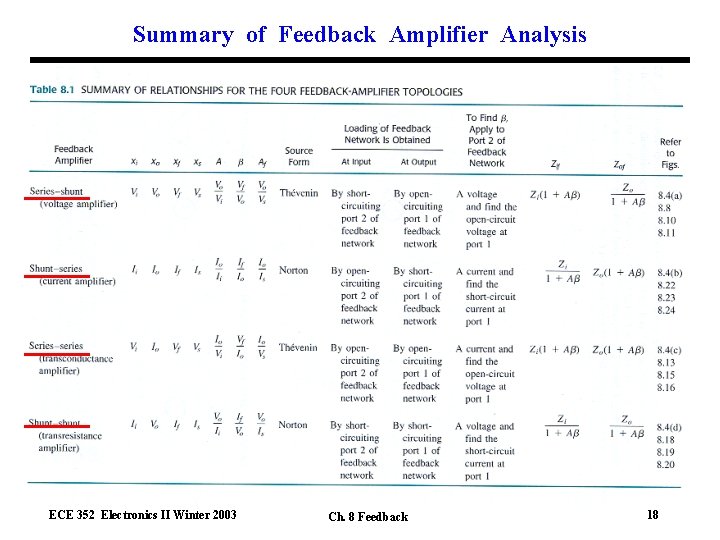
Summary of Feedback Amplifier Analysis ECE 352 Electronics II Winter 2003 Ch. 8 Feedback 18