SHUNT DC MOTOR o Shunt motor its field

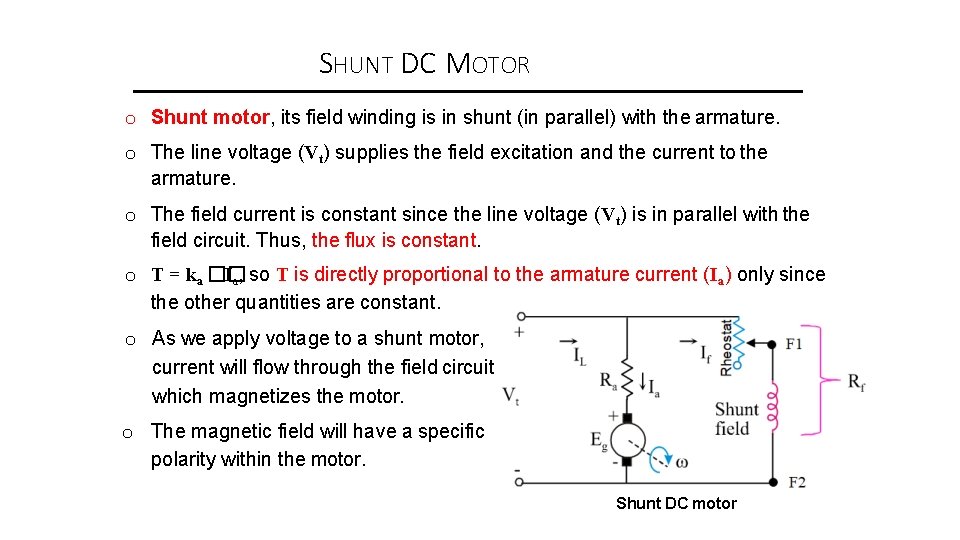
SHUNT DC MOTOR o Shunt motor, its field winding is in shunt (in parallel) with the armature. o The line voltage (Vt) supplies the field excitation and the current to the armature. o The field current is constant since the line voltage (Vt) is in parallel with the field circuit. Thus, the flux is constant. o T = ka �� Ia, so T is directly proportional to the armature current (Ia) only since the other quantities are constant. o As we apply voltage to a shunt motor, current will flow through the field circuit which magnetizes the motor. o The magnetic field will have a specific polarity within the motor. Shunt DC motor

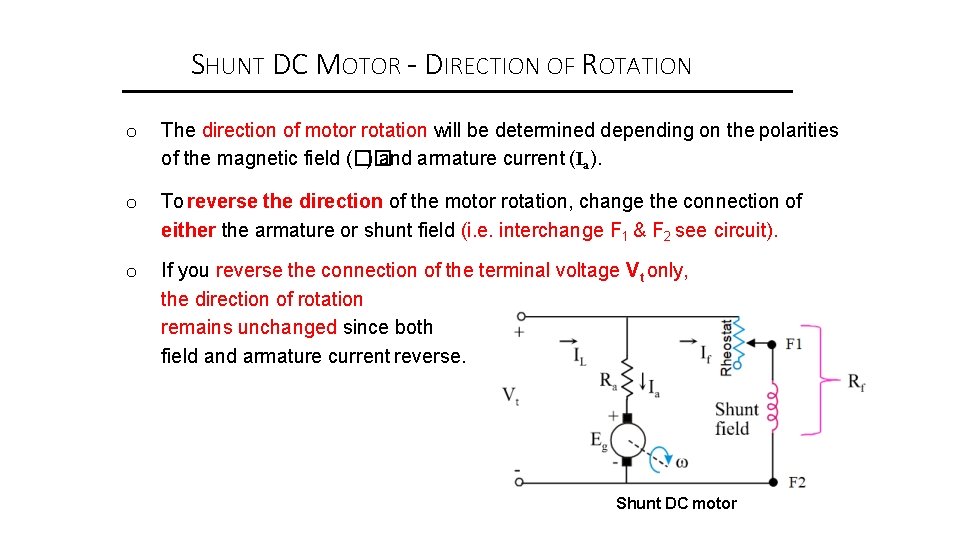
SHUNT DC MOTOR - DIRECTION OF ROTATION o The direction of motor rotation will be determined depending on the polarities of the magnetic field (�� ) and armature current (Ia). o To reverse the direction of the motor rotation, change the connection of either the armature or shunt field (i. e. interchange F 1 & F 2 see circuit). o If you reverse the connection of the terminal voltage Vt only, the direction of rotation remains unchanged since both field and armature current reverse. Shunt DC motor

EFFECT OF LOAD ON THE SHUNT DC MOTOR Torque o As the load increases, so does the torque until it is equal to the new load. Rated Torque Rated Current o The Ia is proportional to the motor torque as well as the load torque. T = k a ϕ Ia Vt − I a R a Vt Ra = − Ia ka ϕ o Only �� and Ia vary since the other quantities are constant. o As load increases, Ia increases, the speed decreases. Shunt DC Motors has excellent speed regulation. Rated Speed Rated Current k a ϕ ω = Vt − I a R a ⇒ ω= Armature current Speed (rad/s) o Remember that Eg = ka �� and Eg = Vt – Ia. Ra, so the angular speed Ia (A) 20

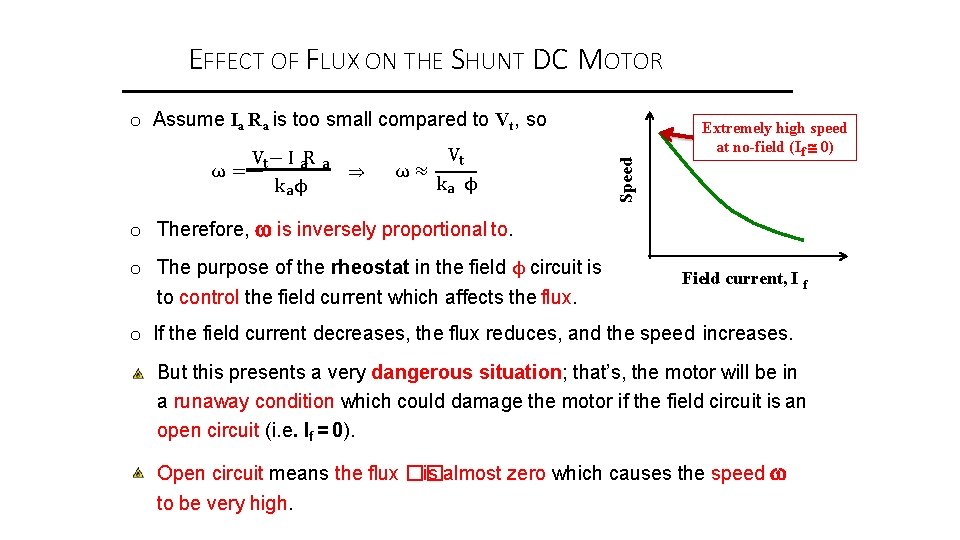
EFFECT OF FLUX ON THE SHUNT DC MOTOR Vt − I a. R ω= ka ϕ a ⇒ Vt ω≈ ka ϕ Speed o Assume Ia Ra is too small compared to Vt, so Extremely high speed at no-field (If 0) o Therefore, is inversely proportional to. o The purpose of the rheostat in the field ϕ circuit is to control the field current which affects the flux. Field current, I f o If the field current decreases, the flux reduces, and the speed increases. But this presents a very dangerous situation; that’s, the motor will be in a runaway condition which could damage the motor if the field circuit is an open circuit (i. e. If = 0). Open circuit means the flux �� is almost zero which causes the speed to be very high.

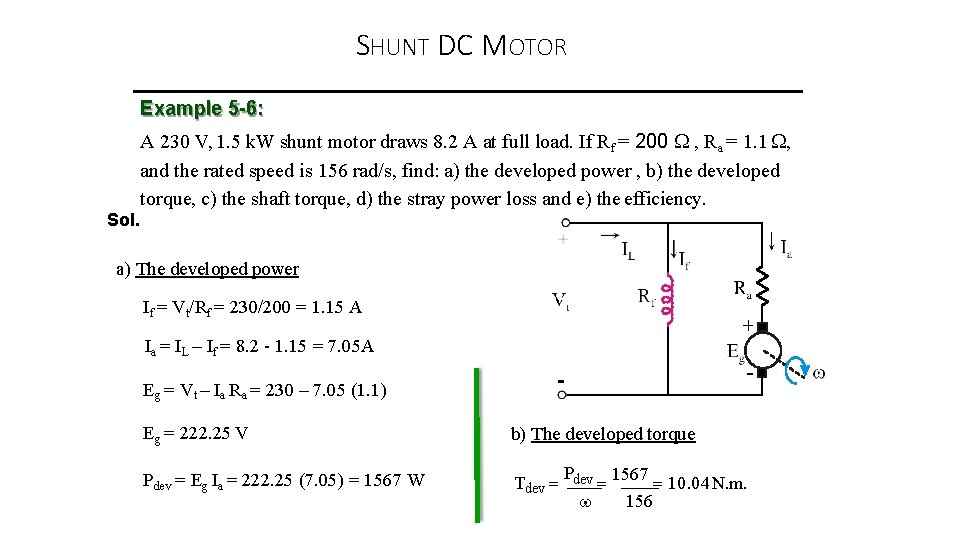
SHUNT DC MOTOR Example 5 -6: A 230 V, 1. 5 k. W shunt motor draws 8. 2 A at full load. If Rf = 200 , Ra = 1. 1 , and the rated speed is 156 rad/s, find: a) the developed power , b) the developed torque, c) the shaft torque, d) the stray power loss and e) the efficiency. Sol. a) The developed power If = Vt/Rf = 230/200 = 1. 15 A Ia = IL – If = 8. 2 - 1. 15 = 7. 05 A Eg = Vt – Ia Ra = 230 – 7. 05 (1. 1) Eg = 222. 25 V b) The developed torque Pdev = Eg Ia = 222. 25 (7. 05) = 1567 W P 1567 Tdev 10. 04 N. m. 156

SHUNT DC MOTOR Example 5 -6: Sol. A 230 V, 1. 5 k. W shunt motor draws 8. 2 A at full load. If Rf = 200 , Ra = 1. 1 , and the rated speed is 156 rad/s, find: a) the developed power , b) the developed torque, c) the shaft torque, d) the stray power loss and e) the efficiency. c) The shaft (output) torque P To o 1500 To 9. 62 N. m. 156 d) The stray power loss Pst = Pdev –Po Pst = 1567 – 1500 = 67 W Pi Pdev=Eg Ia Pcu Po Pst e) The efficiency Pi = Vt IL Pi = 230 x 8. 2 = 1886 W Po %η = x 100 Pi 1. 5 x 103 %η = x 100 = 79. 5% 1886 23

SHUNT DC MOTOR Example 5 -7: Armature of a 6 -pole, 6 -circuits D. C. shunt motor takes 400 A at a speed of 350 rpm. The flux per pole is 80 m. Wb, the number of armature turns is 600, and 3% of the developed torque is lost in windage, friction and iron-loss. Calculate the brake-horse-power. Pdev=Eg Ia Pi Po Sol. Eg = NP πa Pcu ϕω 600 × 6 × 80 × 10− 3 × 350 2π × = 560 V Eg = 60 π× 6 ⇒ Pdev Eg I a Tdev To 0. 97 Tdev 5928. 2 N m Po To 350 560 400 6111. 5 N m 2 350 60 2 5928. 2 217. 28 k. W 60 or 291. 3 hp Pst = 3%Pdev Po = 97 %Pdev

SERIES DC MOTOR o Series motor, its field winding is in series with the armature: IL = Is = Ia o Since they are in series, the flux ϕ is proportional Ia. o As Ia changes with the load, the flux will be affected as well. o Series motors are well-suited for high-torque loads like portable electric tools, cranes, winches, hoists, and automobile starters because of their high torque production and compact size. T = k a ϕI a = k ′ I 2 a

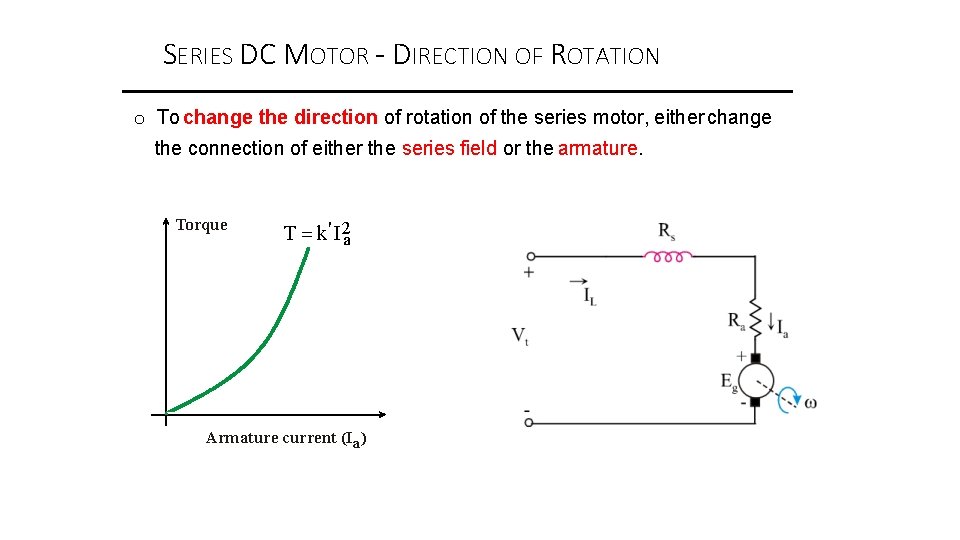
SERIES DC MOTOR - DIRECTION OF ROTATION o To change the direction of rotation of the series motor, either change the connection of either the series field or the armature. Torque T k' I 2 a Armature current (Ia)

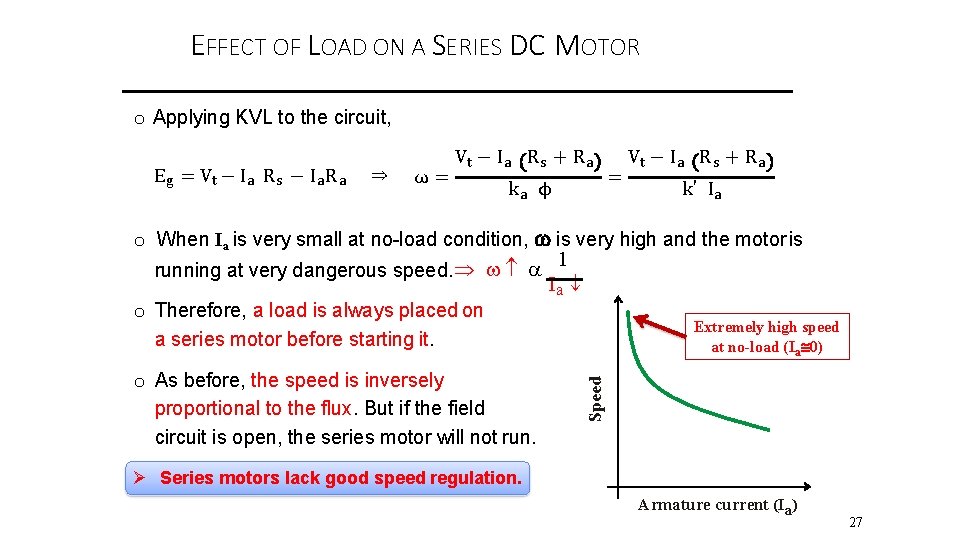
EFFECT OF LOAD ON A SERIES DC MOTOR o Applying KVL to the circuit, Eg = Vt − Ia R s − I a R a ⇒ ω= Vt − Ia R s + R a ka ϕ = Vt − Ia R s + R a k ′ Ia o When Ia is very small at no-load condition, is very high and the motor is 1 running at very dangerous speed. Ia o Therefore, a load is always placed on a series motor before starting it. Speed o As before, the speed is inversely proportional to the flux. But if the field circuit is open, the series motor will not run. Extremely high speed at no-load (Ia 0) Series motors lack good speed regulation. Armature current (Ia) 27

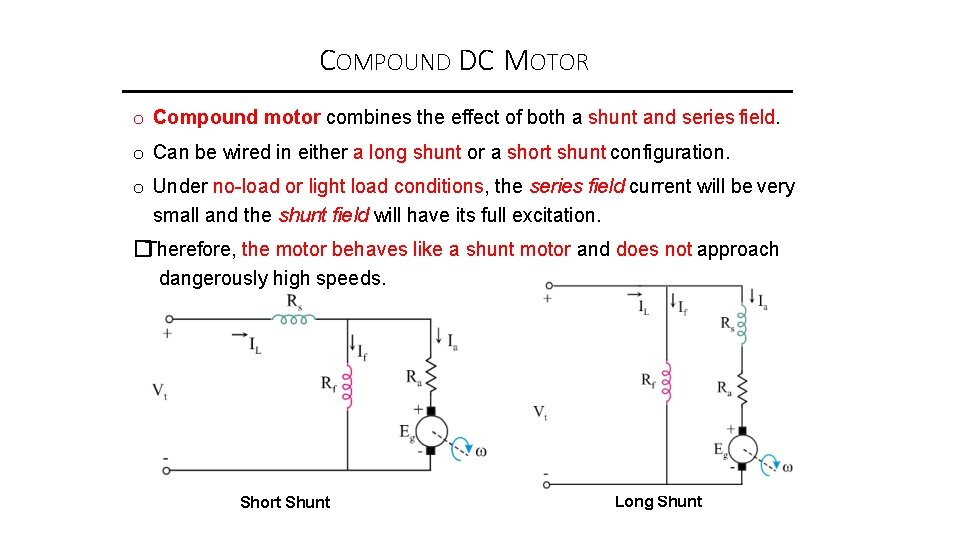
COMPOUND DC MOTOR o Compound motor combines the effect of both a shunt and series field. o Can be wired in either a long shunt or a short shunt configuration. o Under no-load or light load conditions, the series field current will be very small and the shunt field will have its full excitation. �Therefore, the motor behaves like a shunt motor and does not approach dangerously high speeds. Short Shunt Long Shunt

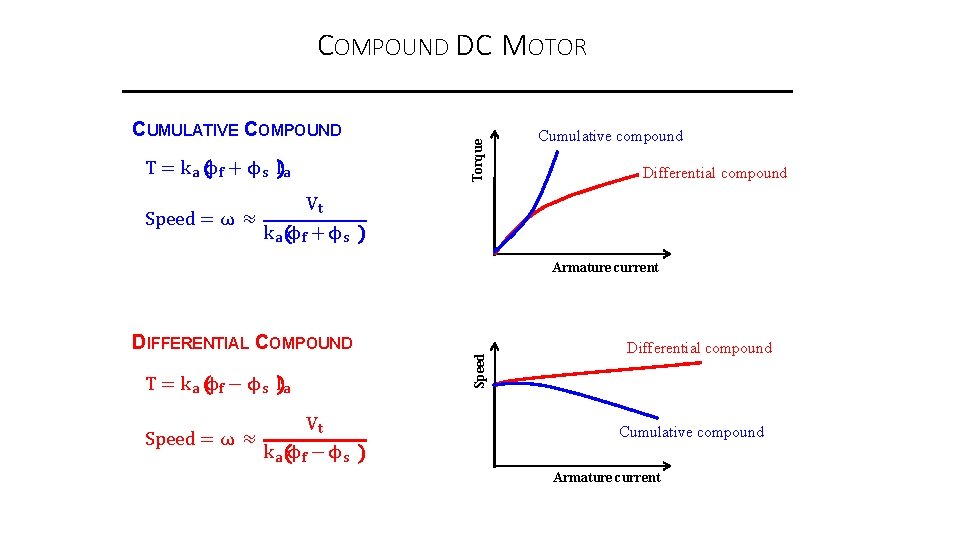
DIFFERENTIAL COMPOUND DC MOTOR o Differential Compound: the series and shunt field windings are connected in such a way that their fields oppose each other. Vt k a ϕf − ϕs o where �� f represents the shunt field flux and �� s represents the series field flux. T = k a ϕf − ϕs Ia Speed = ω ≈ o As the load increases, both Ia and �� s will increase, causing the term (�� f - �� s) decreases, the increase in current predominates over the decrease in flux. o Thus, the induced torque (T) will increase and the motor speed will increase too, and the motor may reach an unsafe uncontrollable speed or "run away" very quickly. (undesirable and dangerous). o The differential compound motor maintains even better constant speed within its load limit than the shunt motor. But it has very poor starting torque and is unable to handle serious overloads. The differential compound motor has very few practical applications.

CUMULATIVE COMPOUND DC MOTOR o Cumulative Compound: the shunt and series windings are connected so that their respective fields aid each other. Vt Speed = ω ≈ T = k a ϕf + ϕs Ia k a ϕf + ϕs o As the load increases, the mmf of the series increases but the mmf of the shunt field remains constant. The total mmf is greater under load that at no-load. o An increase in load causes Ia to increase, producing a larger torque (T) which is greater than the shunt and the net flux will increase as well. o The motor speed falls with increasing load and the speed drop from no-load to full-load. o The cumulative compound motor has somewhat higher starting torque than a shunt motor of the same rating. Compounding improves the torque characteristic and degrades the speed characteristic. 30

CUMULATIVE COMPOUND T = k a ϕf + ϕs Ia Torque COMPOUND DC MOTOR Cumulative compound Differential compound Vt Speed = ω ≈ k a ϕf + ϕs DIFFERENTIAL COMPOUND T = k a ϕf − ϕs Ia Vt Speed = ω ≈ k a ϕf − ϕs Speed Armature current Differential compound Cumulative compound Armature current

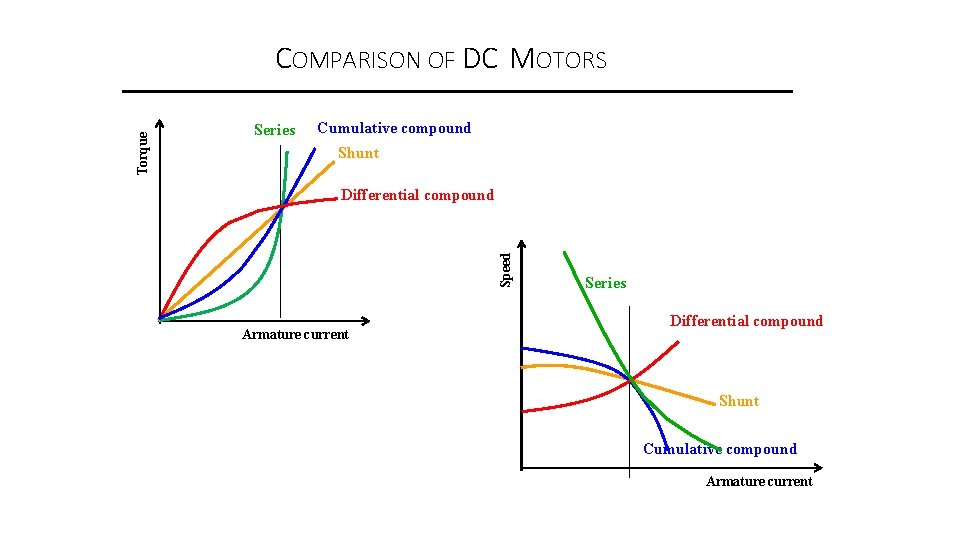
Series Cumulative compound Shunt Differential compound Speed Torque COMPARISON OF DC MOTORS Armature current Series Differential compound Shunt Cumulative compound Armature current

STARTING DC MOTORS If we examine the 120 V/10 A shunt DC motor shown in the figure and calculate the currents at starting, the need for a special device becomes apparent. At starting the speed ( is zero, the back EMF (Eg) is zero. Thus, I a _ start If Vt E g Ra 120 0 1 120 A Vt 120 2 A Rf 60 IL _ start Ia _ start If 122 A IL _ start 122 %Increase 100 1220% Istarting 12 I rated 10 This not only might damage the source, but the motor brushes would most likely burn up. In addition, the motor’s armature winding which is rated at 10 A, would burn. I L _ rated

STARTING DC MOTORS If we examine the 120 V/10 A shunt DC motor shown in the figure and calculate the currents at starting, the need for a special device becomes apparent. At starting the speed ( is zero, the back EMF (Eg) is zero. Thus, Vt − Eg 120 − 0 = = 120 A I a_start = Ra 1 Vt 120 If = = = 2 A Rf 60 I L_start = I a_start + If = 122 A %Increase = I L_start I L_rated 122 × 100 = 10 × 100 = 1220% ⇒ Istarting ≅ 12 × I rated This not only might damage the source, but the motor brushes would most likely burn up. In addition, the motor’s armature winding which is rated at 10 A, would burn. 34

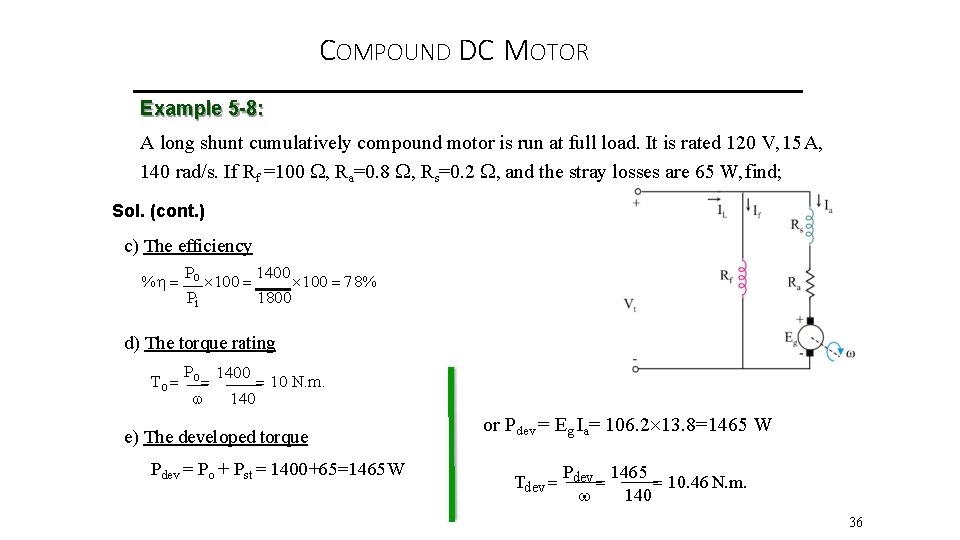
COMPOUND DC MOTOR Example 5 -8: A long shunt cumulatively compound motor is run at full load. It is rated 120 V, 15 A, 140 rad/s. If Rf =100 , Ra=0. 8 , Rs=0. 2 , and the stray losses are 65 W, find; Sol. a) The back EMF Pi If = Vt/Rf =120/100 = 1. 2 A Po Pdev Pcu Pst Ia = IL – If = 15 -1. 2 = 13. 8 A Eg = Vt – Ia (Rs+Ra) = 120 -13. 8(0. 2+0. 8)=106. 2 V b) The output power rating Po = Pin –PLosses Pcu Pst I 2 R f Ia 2 R P a s st f PLosses I 2 f R f Ia 2 R a R s Pst P Losses 1. 22 100 13. 82 0. 8 0. 2 65 399. 44 W Pi Vt IL 120 15 1800 W Po 1800 399. 44 1400. 54 W 1400 W 35

COMPOUND DC MOTOR Example 5 -8: A long shunt cumulatively compound motor is run at full load. It is rated 120 V, 15 A, 140 rad/s. If Rf =100 , Ra=0. 8 , Rs=0. 2 , and the stray losses are 65 W, find; Sol. (cont. ) c) The efficiency % Po 100 1400 100 78% Pi 1800 d) The torque rating P 1400 To o 10 N. m. 140 e) The developed torque Pdev = Po + Pst = 1400+65=1465 W or Pdev = Eg Ia= 106. 2 13. 8=1465 W P 1465 Tdev 10. 46 N. m. 140 36

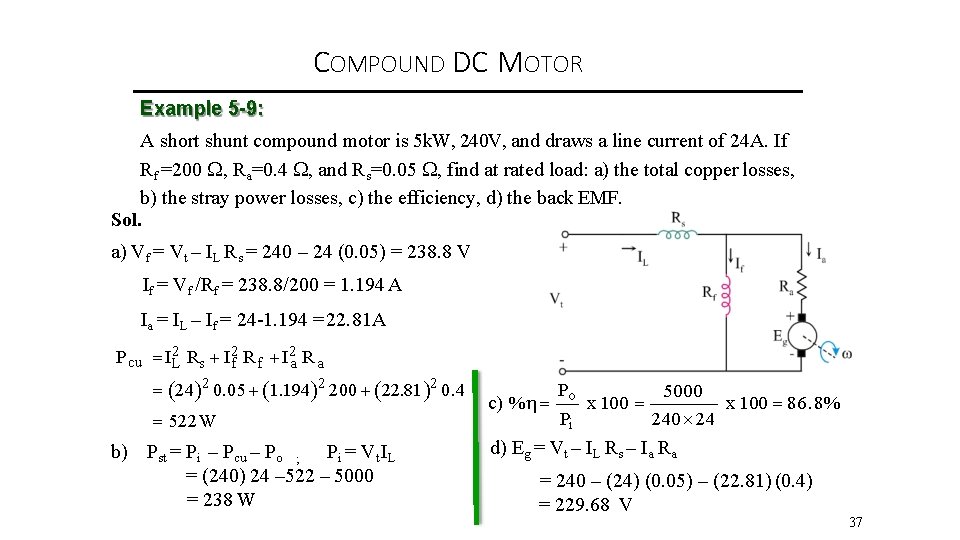
COMPOUND DC MOTOR Example 5 -9: A short shunt compound motor is 5 k. W, 240 V, and draws a line current of 24 A. If Rf =200 , Ra=0. 4 , and Rs=0. 05 , find at rated load: a) the total copper losses, b) the stray power losses, c) the efficiency, d) the back EMF. Sol. a) Vf = Vt – IL Rs = 240 – 24 (0. 05) = 238. 8 V If = Vf /Rf = 238. 8/200 = 1. 194 A Ia = IL – If = 24 -1. 194 = 22. 81 A Pcu IL 2 Rs If 2 R f I 2 a R a 24 2 0. 05 1. 194 2 200 22. 81 2 0. 4 522 W b) Pst = Pi – Pcu – Po ; Pi = Vt IL = (240) 24 – 522 – 5000 = 238 W P 5000 c) % o x 100 86. 8% Pi 240 24 d) Eg = Vt – IL Rs – Ia Ra = 240 – (24) (0. 05) – (22. 81) (0. 4) = 229. 68 V 37

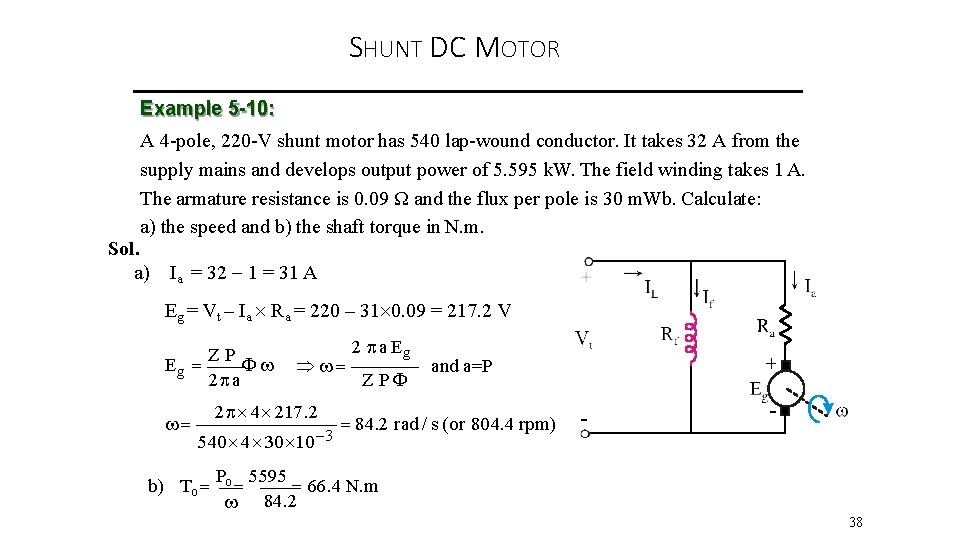
SHUNT DC MOTOR Example 5 -10: A 4 -pole, 220 -V shunt motor has 540 lap-wound conductor. It takes 32 A from the supply mains and develops output power of 5. 595 k. W. The field winding takes 1 A. The armature resistance is 0. 09 Ω and the flux per pole is 30 m. Wb. Calculate: a) the speed and b) the shaft torque in N. m. Sol. a) Ia = 32 1 = 31 A Eg = Vt – Ia Ra = 220 – 31 0. 09 = 217. 2 V ZP Eg 2 a 2 4 217. 2 540 4 30 10 3 2 a Eg Z P and a=P 84. 2 rad / s (or 804. 4 rpm) P 5595 b) To o 66. 4 N. m 84. 2 38

Lecture # 6