Shortest Paths Weighted Graphs In a weighted graph

Shortest Paths

Weighted Graphs • In a weighted graph, each edge has an associated numerical value, called the weight of the edge • Edge weights may represent, distances, costs, etc. Example: – A vertex represents an airport and stores the three-letter airport code – An edge represents a flight route between two airports and stores the mileage of the route Providence Chicago San Francisco SFO HNL 2555 337 Honolulu LAX Los Angeles 1843 3 4 17 1233 849 ORD 802 • 7 138 DFW Dallas 1120 PVD 2 14 LGA New York 10 99 MIA Miami 2

Shortest Paths • Weight of the path P sum of the weights of all the edges on the path P • Shortest path with smallest weight • The problem: Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight (shortest path) between u and v. 3

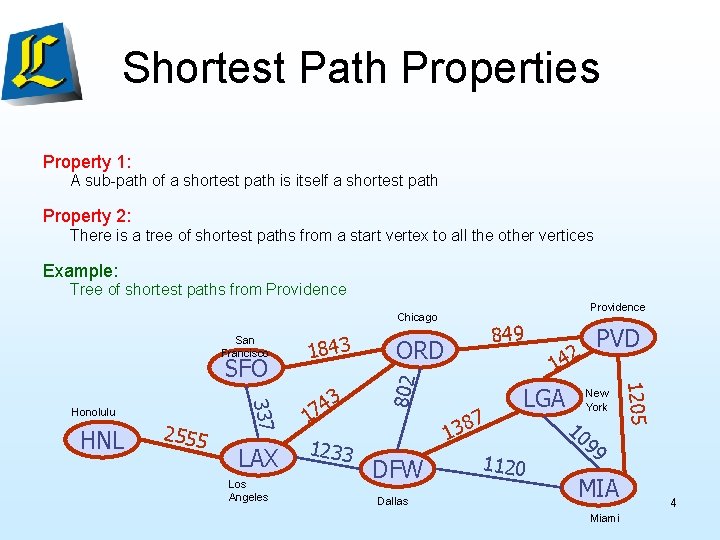
Shortest Path Properties Property 1: A sub-path of a shortest path is itself a shortest path Property 2: There is a tree of shortest paths from a start vertex to all the other vertices Example: Tree of shortest paths from Providence Chicago SFO LAX Los Angeles 3 74 1 1233 849 ORD DFW Dallas 7 8 3 1 2 PVD 14 LGA 1120 10 New York 1205 HNL 2555 337 Honolulu 1843 802 San Francisco 99 MIA Miami 4

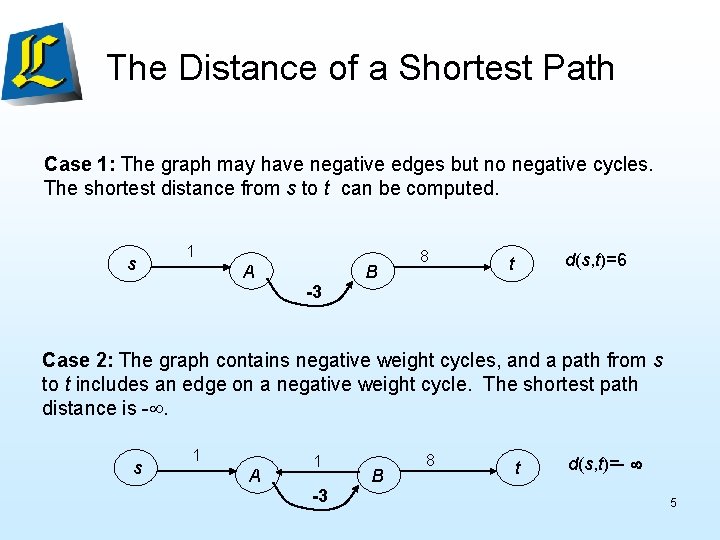
The Distance of a Shortest Path Case 1: The graph may have negative edges but no negative cycles. The shortest distance from s to t can be computed. s 1 A B 8 d(s, t)=6 t -3 Case 2: The graph contains negative weight cycles, and a path from s to t includes an edge on a negative weight cycle. The shortest path distance is -. s 1 A 1 -3 B 8 t d(s, t)=- 5

Shortest Path Algorithms • Dijkstra’s algorithm does NOT allow negative edges. – Uses a greedy heuristic. – undirected/directed graph • Bellman-Ford’s and Floyd’s algorithms work correctly for any graph and can detect negative cycles. – Must be directed graph if negative edges are included. 6

Shortest Path Algorithms • Dijkstra’s algorithm does NOT allow negative edges. – Uses a greedy heuristic. – undirected/directed graph • Bellman-Ford’s and Floyd’s algorithms work correctly for any graph and can detect negative cycles. – Must be directed graph if negative edges are included. We will study Dijkstra’s algorithm only. The others are beyond the scope of this course 7

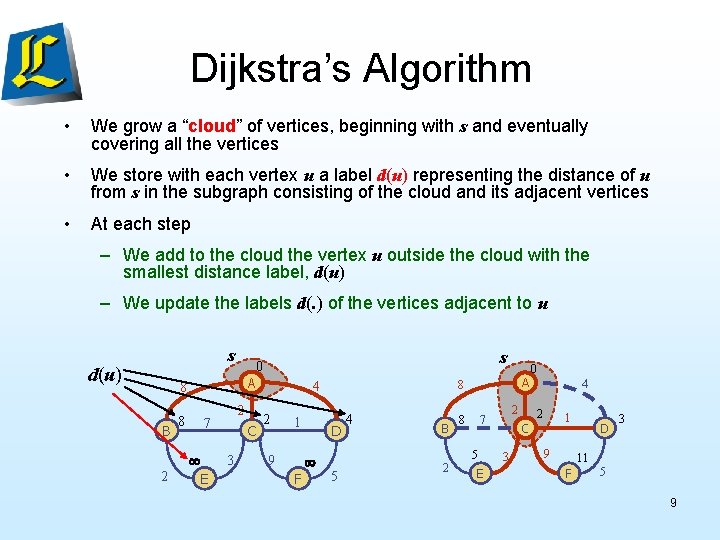
Dijkstra’s Algorithm • The distance of a vertex v from a vertex s is the length of a shortest path between s and v • Dijkstra’s algorithm (pronounced dyke-stra) computes the distances of all the vertices from a given start vertex s • Assumptions: – the graph is connected – the edge weights are nonnegative 8

Dijkstra’s Algorithm • We grow a “cloud” of vertices, beginning with s and eventually covering all the vertices • We store with each vertex u a label d(u) representing the distance of u from s in the subgraph consisting of the cloud and its adjacent vertices • At each step – We add to the cloud the vertex u outside the cloud with the smallest distance label, d(u) – We update the labels d(. ) of the vertices adjacent to u s d(u) A 8 B 2 s 0 8 2 7 C 3 E 4 2 1 9 F 8 D A 5 4 B 2 2 7 8 5 E C 3 0 4 2 1 9 D 3 11 F 5 9

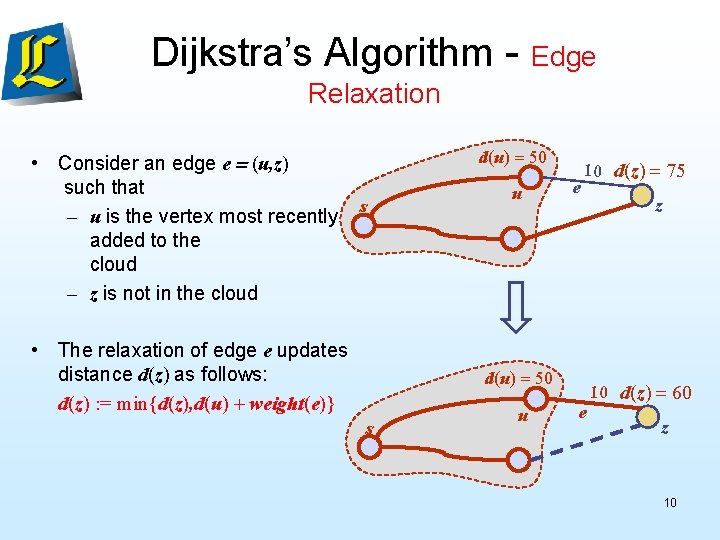
Dijkstra’s Algorithm - Edge Relaxation • Consider an edge e = (u, z) such that – u is the vertex most recently added to the cloud – z is not in the cloud d(u) = 50 s • The relaxation of edge e updates distance d(z) as follows: d(z) : = min{d(z), d(u) + weight(e)} u e 10 d(z) = 75 d(u) = 50 s u e z 10 d(z) = 60 z 10

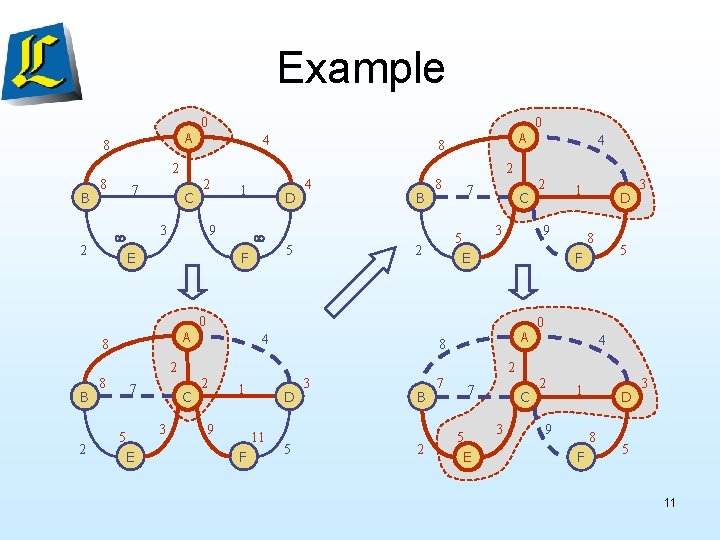
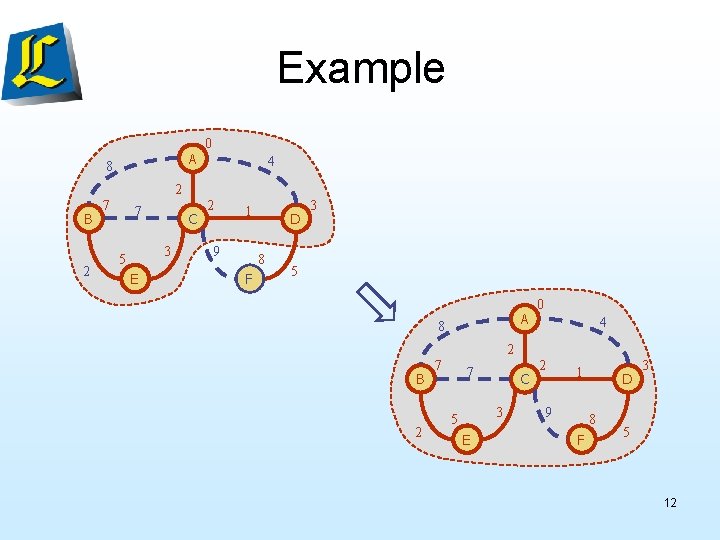
Example A 8 0 4 A 8 2 B 8 7 2 C 2 1 9 E D F A 8 4 5 B 8 7 3 5 2 C B 2 7 E D 8 5 F A 8 3 0 4 2 C 3 5 1 9 0 4 2 E 2 8 4 2 3 0 2 1 9 D 11 F 5 3 B 2 7 7 C 3 5 E 2 1 9 D 8 F 3 5 11

Example A 8 0 4 2 B 2 7 7 C 3 5 E 2 1 9 D 8 F 3 5 12

Dijkstra’s Algorithm • A priority queue stores the vertices outside the cloud (Key: distance, Element: vertex) Algorithm Shortest. Path(G, v) Input A weighted graph G with nonnegative edge weights, and a start vertex v of G Output a label D[u] for each u of G , so that D[u] is the length of a shortest path from v to u in G Initialize D[v] : = 0 , and D[u] : = for every vertex u ≠ v Let a priority queue Q contain all the vertices of G using the D label as a key while Q is not empty do {pull a new vertex u into the cloud} u : = Q. remove. Min() for each vertex z adjacent to u such that z is in Q do {perform the relaxation on edge (u, z)} if D[u] + w((u, z)) < D[z] then D[z] : = D[u] + w((u, z)) change to D[z] the key of vertex z in Q return the label D[u] of each vertex u 13

Analysis of Dijkstra’s Algorithm • Inserting all the vertices in Q with their initial key value can be done in O(n log n) • At each iteration of the while loop, – we spend O(log n) time to remove vertex u from Q and – O(degree (v) log n) time to perform the relaxation procedure on each edge //note that it takes log n to update D[z] in the heap • The overall running time for the entire while loop is O(m log n) – remember Sv degree(v) = 2 m • Dijkstra’s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure // the use of adjacency list allows us to step through the vertices adjacent to u during the relaxation step in time proportional to their number 14

Why It Doesn’t Work for Negative-Weight Edges • Dijkstra’s algorithm is based on the idea that it adds vertices by increasing distance. – If a node with a negative incident edge were to be added late to the cloud, it could mess up distances for vertices already in the cloud. A 8 B 2 6 7 7 5 C 0 E 0 4 5 1 -8 F D 9 4 5 C’s true distance is 1, but it is already in the cloud with d(C)=5! 15