Shortest Paths Text Discrete Mathematics and Its Applications






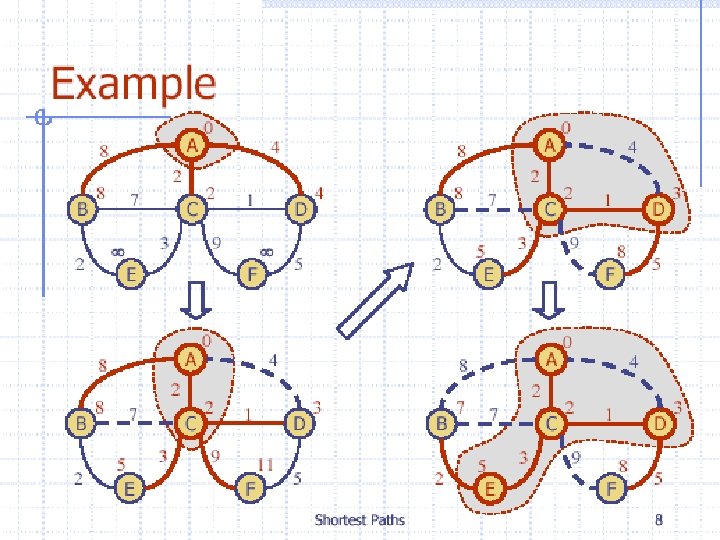












- Slides: 27

Shortest Paths Text Discrete Mathematics and Its Applications (5 Edition) th Kenneth H. Rosen Chapter 10. 6 Based on slides from Chuck Allison, Michael T. Goodrich, and Roberto Tamassia By Longin Jan Latecki

Weighted Graphs that have a number assigned to each edge are called weighted graphs. BOS NY CHI SF DEN ATL LA MIA

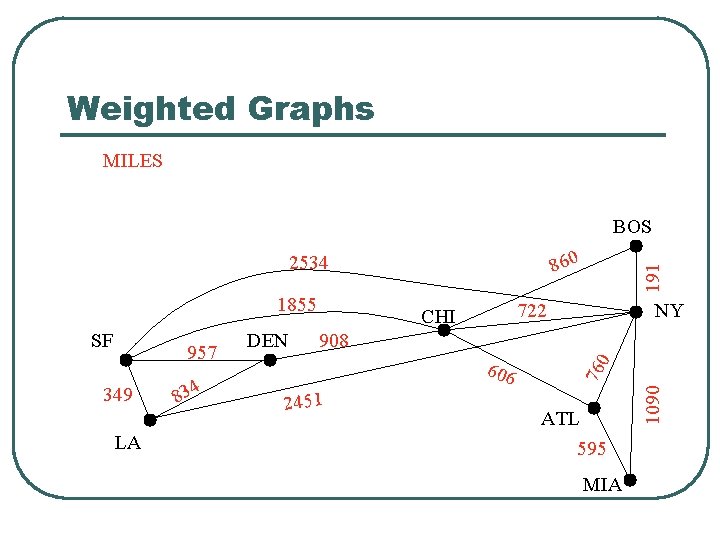
Weighted Graphs MILES BOS 1855 349 LA 4 83 DEN NY 908 606 2451 1090 957 722 CHI 760 SF 191 860 2534 ATL 595 MIA

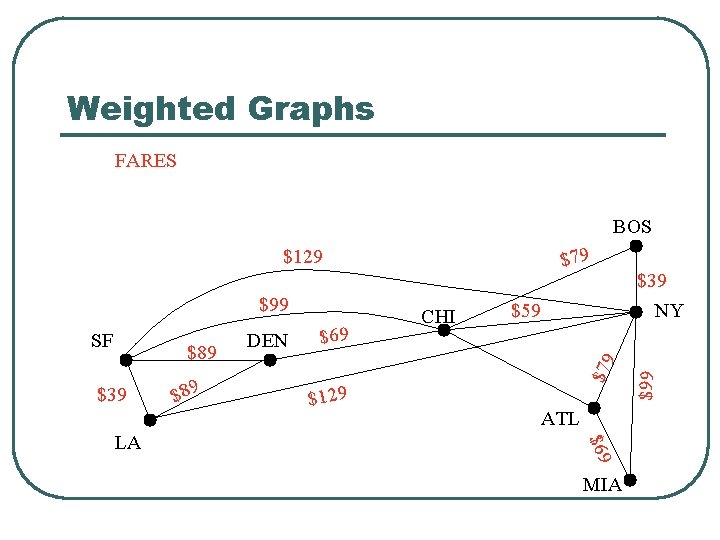
Weighted Graphs FARES BOS SF $89 $39 $69 $129 $59 ATL $69 LA $89 DEN CHI $79 $99 MIA $39 NY $99 $79 $129

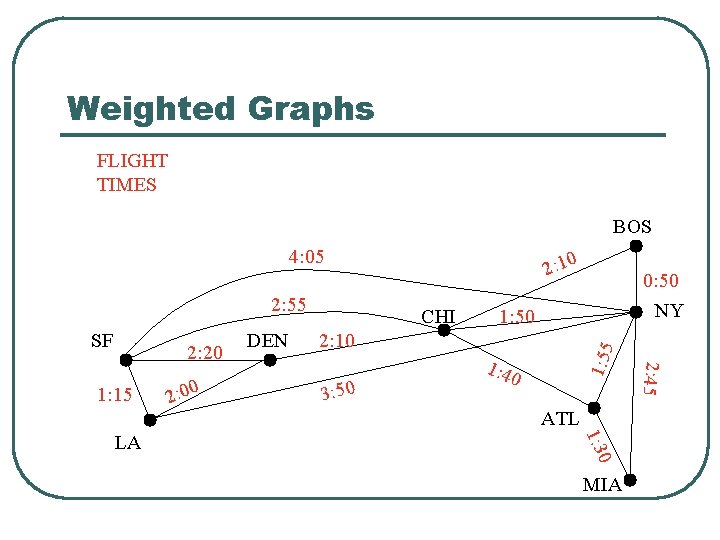
Weighted Graphs FLIGHT TIMES BOS 4: 05 2: 55 1: 15 2: 10 3: 50 1: 4 0 ATL 0 1: 3 LA 2: 00 DEN 1: 50 MIA 2: 45 2: 20 CHI 0: 50 NY 1: 55 SF 2: 10

Weighted Graphs l l A weighted graph is a graph in which each edge (u, v) has a weight w(u, v). Each weight is a real number. Weights can represent distance, cost, time, capacity, etc. The length of a path in a weighted graph is the sum of the weights on the edges. Dijkstra’s Algorithm finds the shortest path between two vertices.









Dijkstra Animation l l Youtube video: http: //www. youtube. com/watch? v=gdmf. Owy. Qlc. I Java animation: http: //weierstrass. is. tokushimau. ac. jp/ikeda/suuri/dijkstra/Dijkstra. shtml

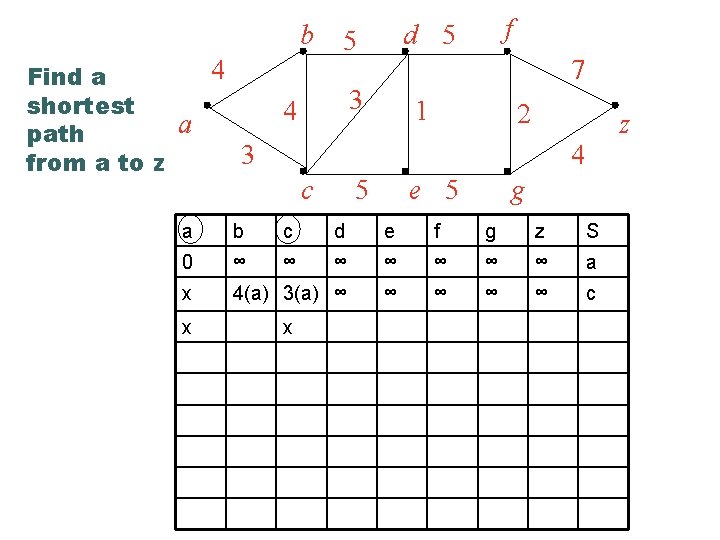
b 4 Find a shortest a path 3 from a to z 5 d 5 3 1 4 f 7 2 z 4 c 5 e 5 g a b c d e f g z S 0 ∞ ∞ ∞ ∞ a x 4(a) 3(a) ∞ ∞ ∞ c x x

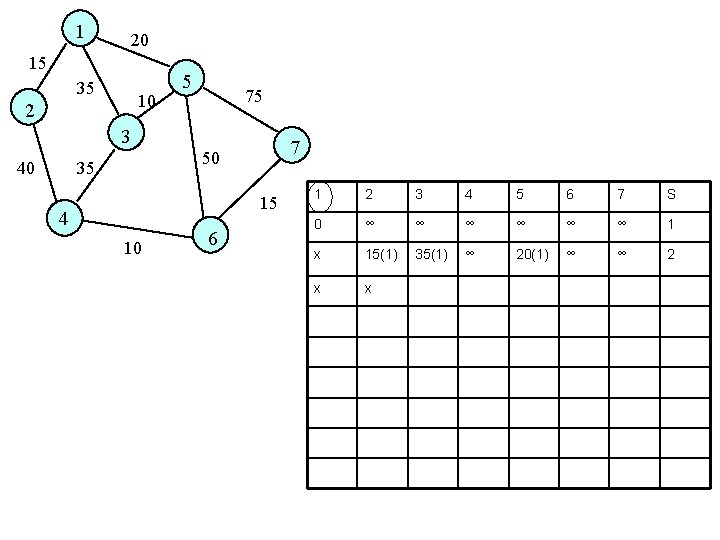
1 20 15 35 10 2 5 75 3 40 7 50 35 15 4 10 6 1 2 3 4 5 6 7 S 0 ∞ ∞ ∞ 1 x 15(1) 35(1) ∞ 20(1) ∞ ∞ 2 x x

Theorems Dijkstra’s algorithm finds the length of a shortest path between two vertices in a connected simple undirected weighted graph G=(V, E). The time required by Dijkstra's algorithm is O(|V|2). It will be reduced to O(|E|log|V|) if heap is used to keep {v VSi : L(v) < }, where Si is the set S after iteration i.

The Traveling Salesman Problem l. The traveling salesman problem is one of the classical problems in computer science. l. A traveling salesman wants to visit a number of cities and then return to his starting point. Of course he wants to save time and energy, so he wants to determine the shortest cycle for his trip. l. We can represent the cities and the distances between them by a weighted, complete, undirected graph. l. The problem then is to find the shortest cycle (of minimum total weight that visits each vertex exactly one).

The Traveling Salesman Problem l Importance: • • Variety of scheduling application can be solved as a traveling salesmen problem. Examples: • Ordering drill position on a drill press. • School bus routing.

THE FEDERAL EMERGENCY MANAGEMENT AGENCY l A visit must be made to four local offices of FEMA, going out from and returning to the same main office in Northridge, Southern California.

FEMA traveling salesman Network representation

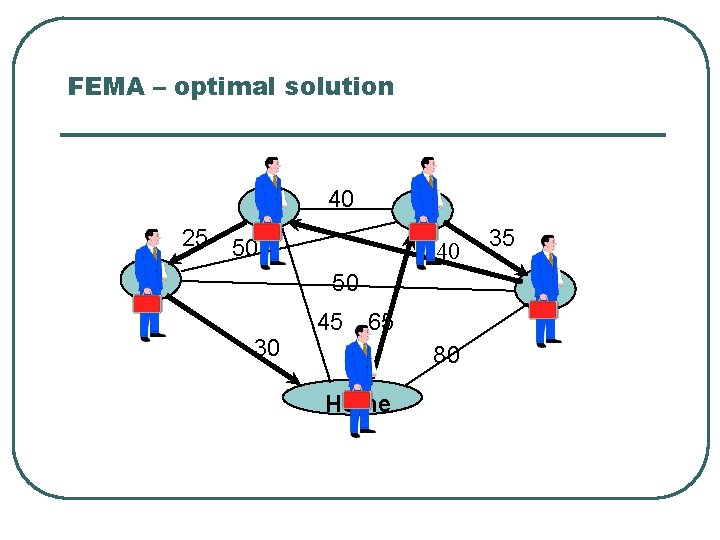
2 40 3 25 35 50 40 50 1 4 45 65 30 80 Home

FEMA - Traveling Salesman • Solution approaches – Enumeration of all possible cycles. • This results in (m-1)! cycles to enumerate for a graph with m nodes. • Only small problems can be solved with this approach.

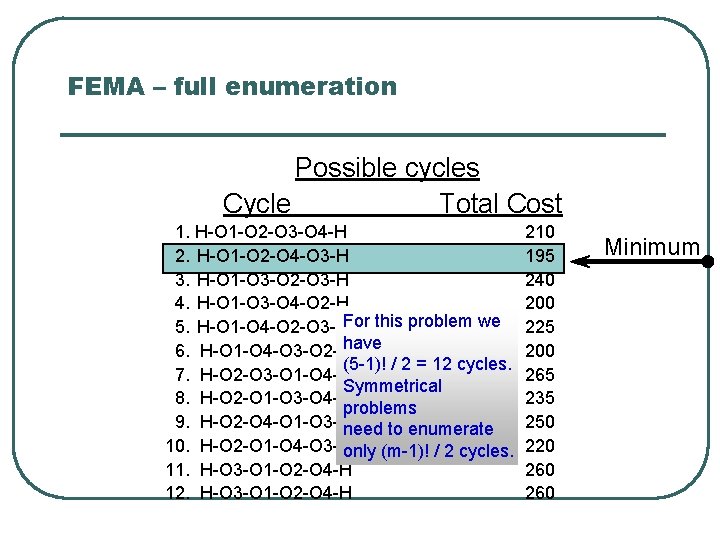
FEMA – full enumeration Possible cycles Cycle Total Cost 1. H-O 1 -O 2 -O 3 -O 4 -H 2. H-O 1 -O 2 -O 4 -O 3 -H 3. H-O 1 -O 3 -O 2 -O 3 -H 4. H-O 1 -O 3 -O 4 -O 2 -H 5. H-O 1 -O 4 -O 2 -O 3 -HFor this problem we 6. H-O 1 -O 4 -O 3 -O 2 -Hhave (5 -1)! / 2 = 12 cycles. 7. H-O 2 -O 3 -O 1 -O 4 -H Symmetrical 8. H-O 2 -O 1 -O 3 -O 4 -H problems 9. H-O 2 -O 4 -O 1 -O 3 -Hneed to enumerate 10. H-O 2 -O 1 -O 4 -O 3 -Honly (m-1)! / 2 cycles. 11. H-O 3 -O 1 -O 2 -O 4 -H 12. H-O 3 -O 1 -O 2 -O 4 -H 210 195 240 200 225 200 265 235 250 220 260 Minimum

FEMA – optimal solution 2 40 3 25 50 1 40 50 30 45 35 4 65 80 Home

The Traveling Salesman Problem l. Finding the shortest cycle is different than Dijkstra’s shortest path. It is much harder too, no algorithm exists with polynomial worst-case time complexity! l. This means that for large numbers of vertices, solving the traveling salesman problem is impractical. l. The problem has theoretical importance because it represents a class of difficult problems known as NP-hard problems. l. In these cases, we can use efficient approximation algorithms that determine a path whose length may be slightly larger than the traveling salesman’s path.