Shortest Paths Text Discrete Mathematics and Its Applications

Shortest Paths Text Discrete Mathematics and Its Applications (5 Edition) th Kenneth H. Rosen Chapter 8. 6 Based on slides from Chuck Allison, Michael T. Goodrich, and Roberto Tamassia By Longin Jan Latecki

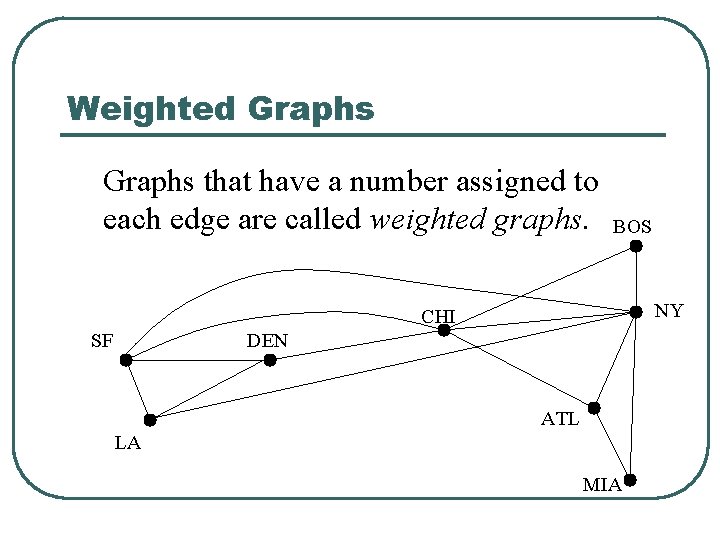
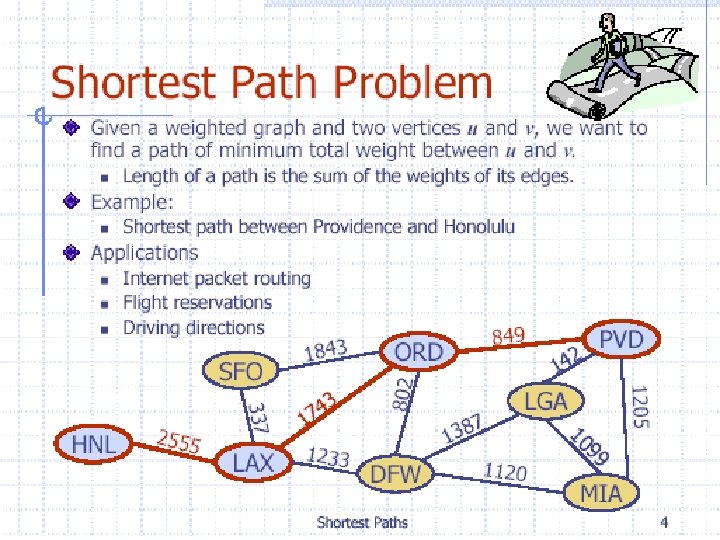
Weighted Graphs that have a number assigned to each edge are called weighted graphs. BOS NY CHI SF DEN ATL LA MIA

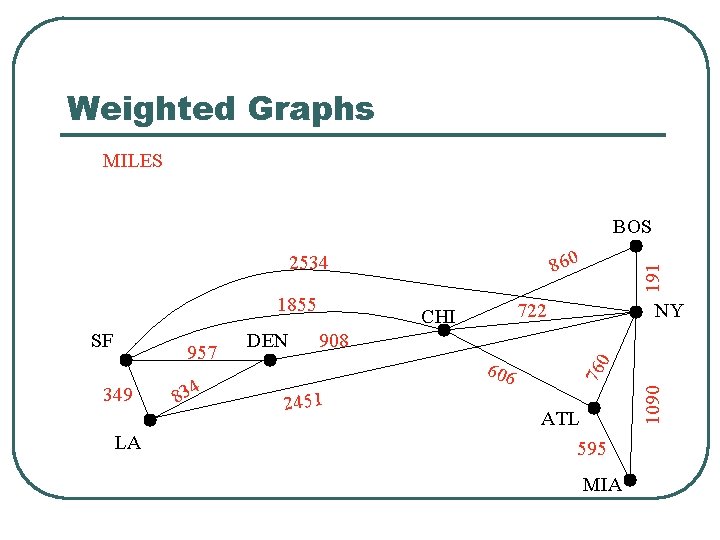
Weighted Graphs MILES BOS 1855 349 LA 4 83 DEN NY 908 606 2451 1090 957 722 CHI 760 SF 191 860 2534 ATL 595 MIA

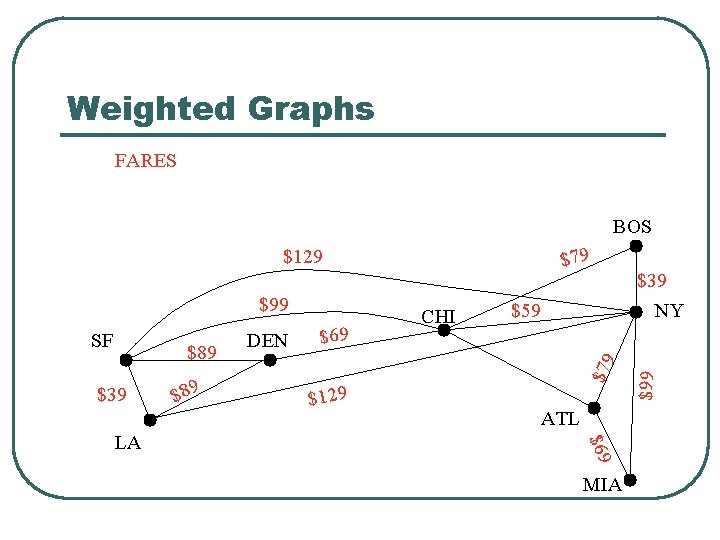
Weighted Graphs FARES BOS SF $89 $39 $69 $129 $59 ATL $69 LA $89 DEN CHI $79 $99 MIA $39 NY $99 $79 $129

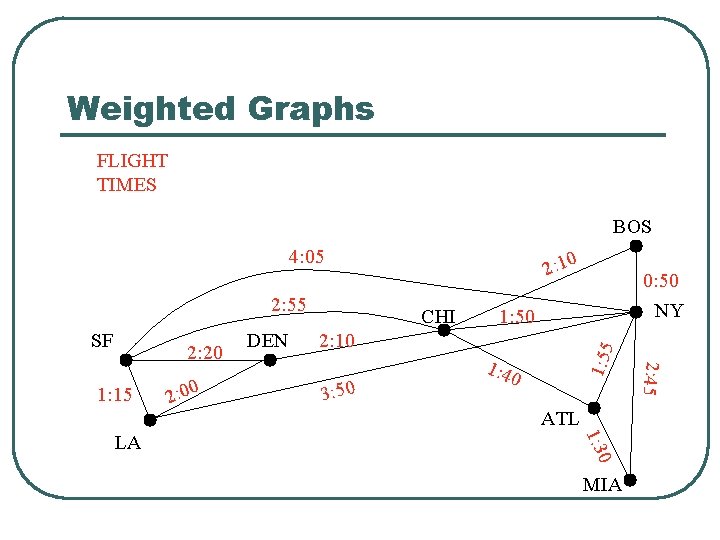
Weighted Graphs FLIGHT TIMES BOS 4: 05 2: 55 1: 15 2: 10 3: 50 1: 4 0 ATL 0 1: 3 LA 2: 00 DEN 1: 50 MIA 2: 45 2: 20 CHI 0: 50 NY 1: 55 SF 2: 10

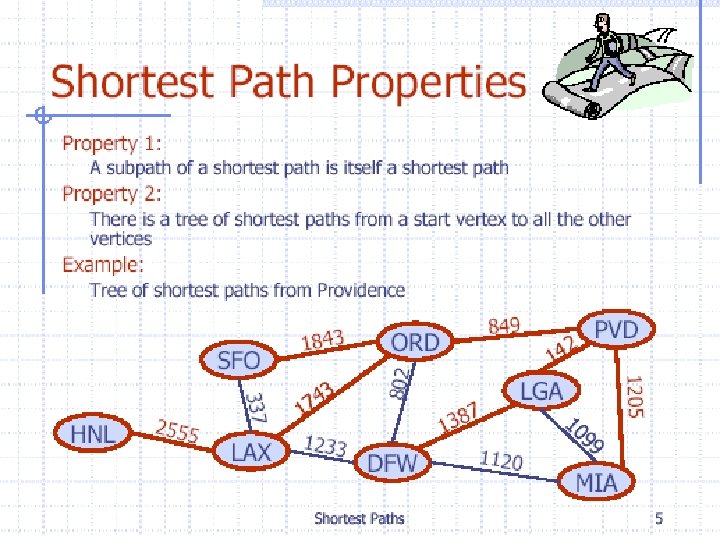
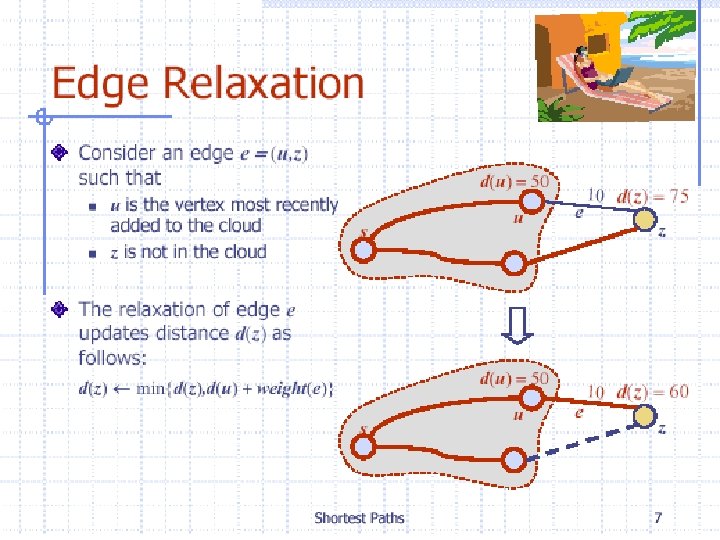
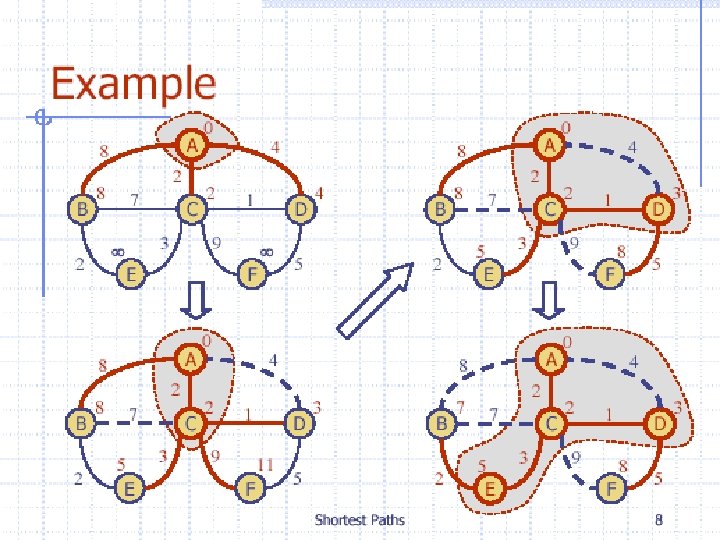
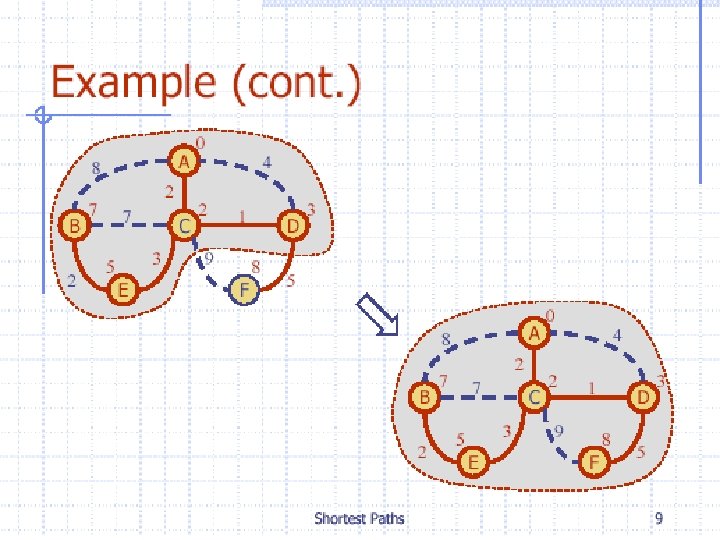
Weighted Graphs l l A weighted graph is a graph in which each edge (u, v) has a weight w(u, v). Each weight is a real number. Weights can represent distance, cost, time, capacity, etc. The length of a path in a weighted graph is the sum of the weights on the edges. Dijkstra’s Algorithm finds the shortest path between two vertices.

Dijkstra's Algorithm

Dijkstra Animation l Demo

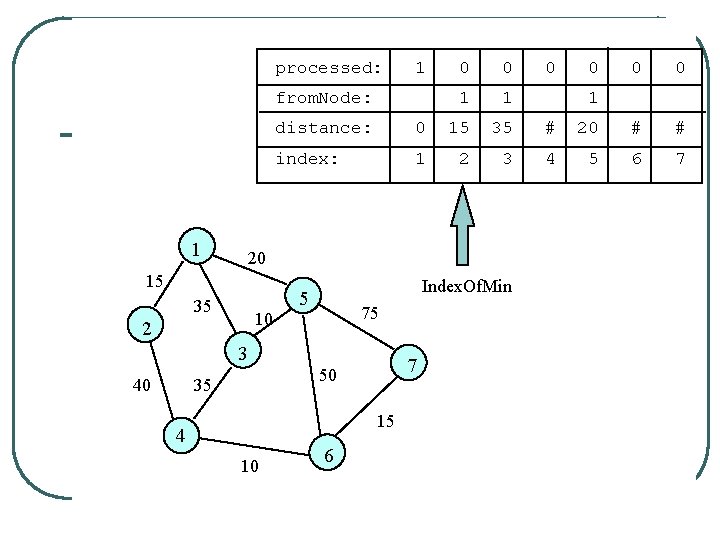
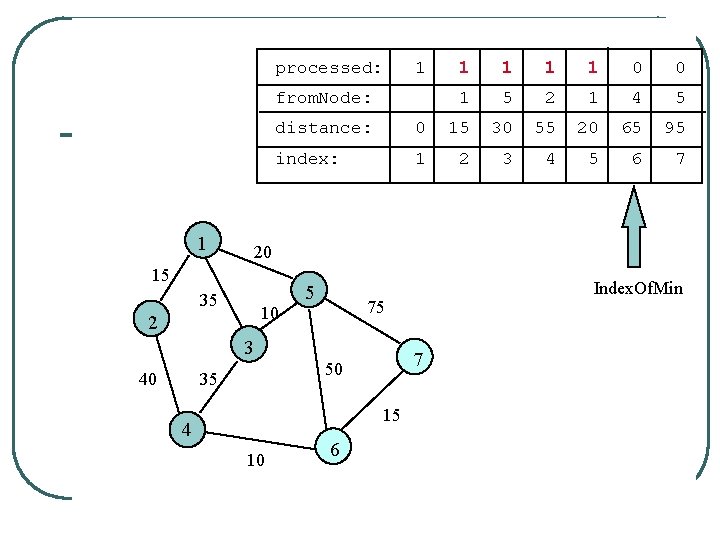
processed: 1 from. Node: 1 0 1 1 35 10 2 0 1 35 # 20 # # index: 1 2 3 4 5 6 7 Index. Of. Min 5 75 7 15 10 0 15 50 4 0 0 3 35 0 distance: 20 15 40 0 6

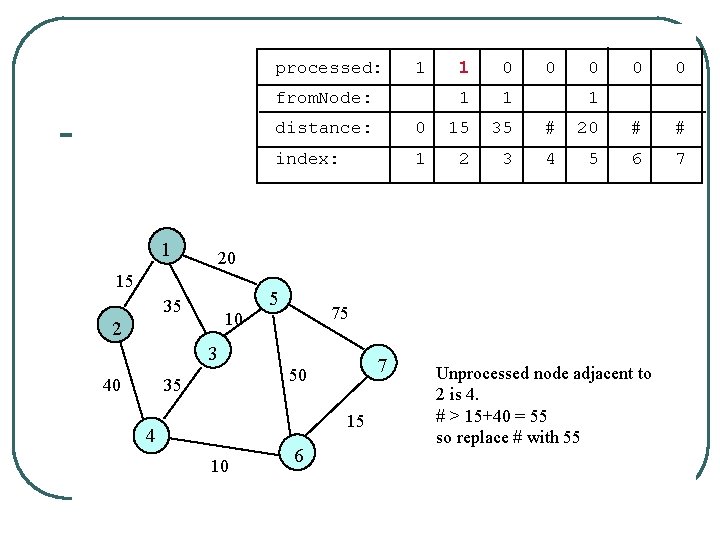
processed: 1 from. Node: 1 0 1 1 0 0 1 distance: 0 15 35 # 20 # # index: 1 2 3 4 5 6 7 20 15 35 10 2 5 75 3 40 1 7 50 35 15 4 10 6 Unprocessed node adjacent to 2 is 4. # > 15+40 = 55 so replace # with 55

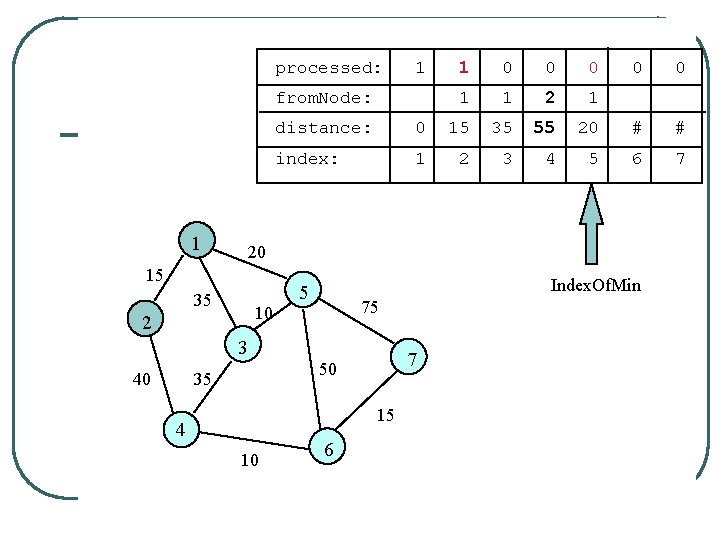
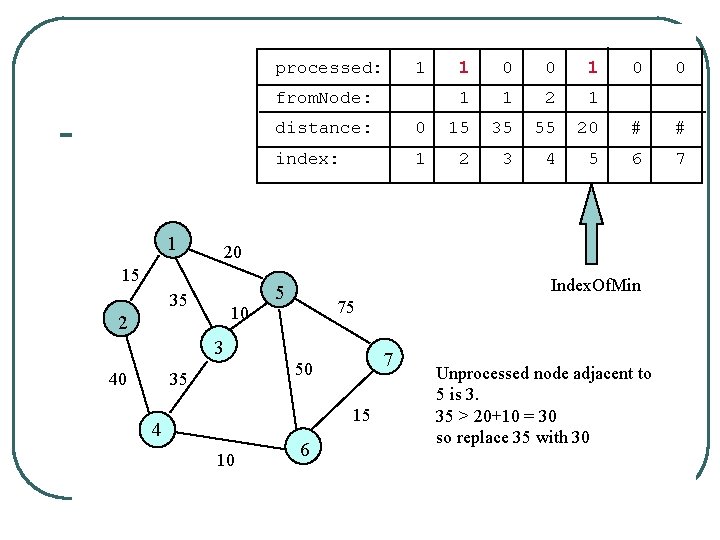
processed: 1 from. Node: 1 0 0 0 1 1 2 1 0 0 distance: 0 15 35 55 20 # # index: 1 2 3 4 5 6 7 20 15 35 10 2 Index. Of. Min 5 75 3 40 1 7 50 35 15 4 10 6

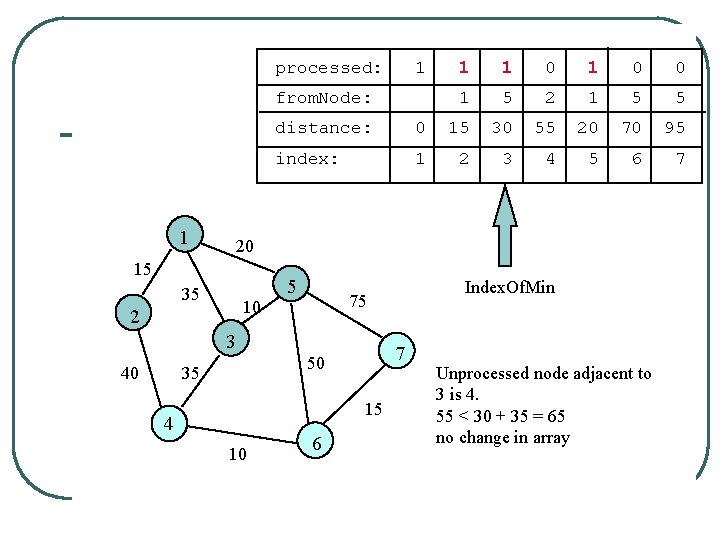
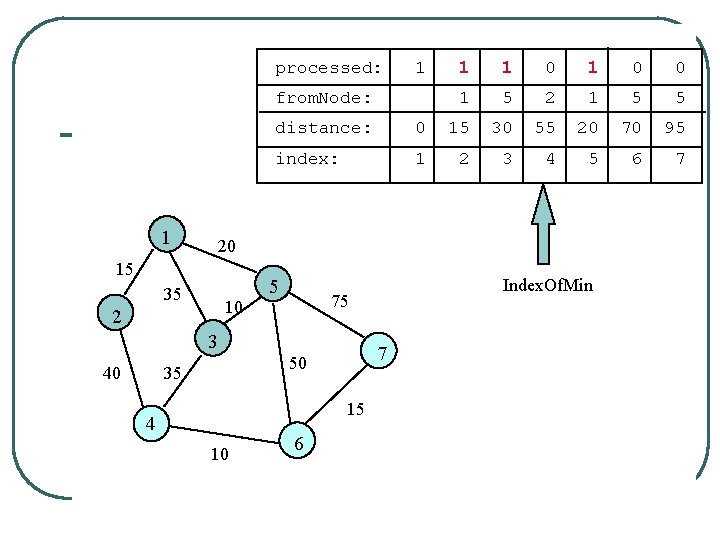
processed: 1 from. Node: 1 0 0 1 1 1 2 1 0 0 distance: 0 15 35 55 20 # # index: 1 2 3 4 5 6 7 20 15 35 10 2 Index. Of. Min 5 75 3 40 1 7 50 35 15 4 10 6 Unprocessed node adjacent to 5 is 3. 35 > 20+10 = 30 so replace 35 with 30

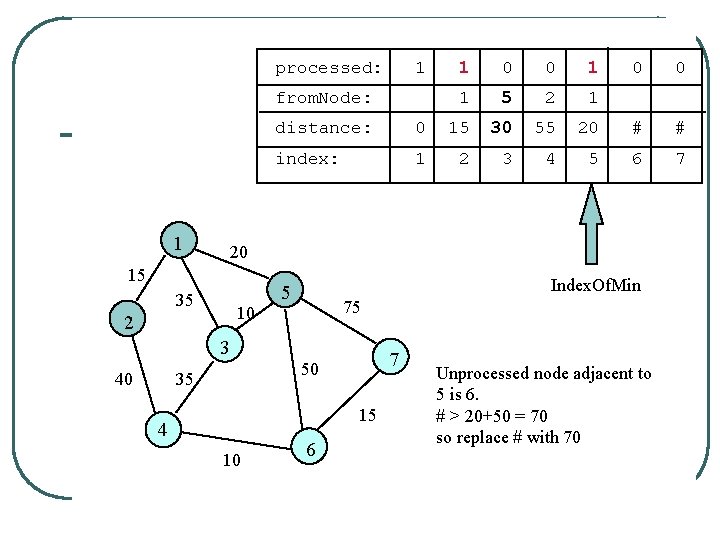
processed: 1 from. Node: 1 0 0 1 1 5 2 1 0 0 distance: 0 15 30 55 20 # # index: 1 2 3 4 5 6 7 20 15 35 10 2 Index. Of. Min 5 75 3 40 1 7 50 35 15 4 10 6 Unprocessed node adjacent to 5 is 6. # > 20+50 = 70 so replace # with 70

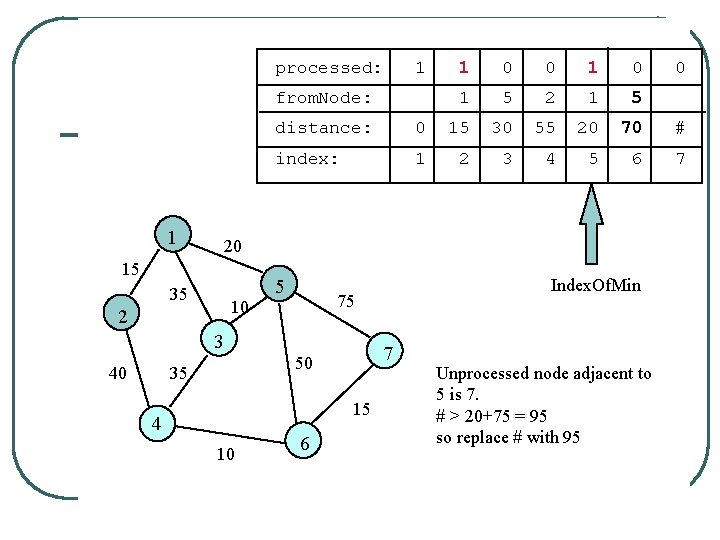
processed: 1 from. Node: 1 0 0 1 5 2 1 5 35 10 2 0 15 30 55 20 70 # index: 1 2 3 4 5 6 7 50 15 4 10 Index. Of. Min 75 3 35 0 distance: 20 15 40 1 6 Unprocessed node adjacent to 5 is 7. # > 20+75 = 95 so replace # with 95

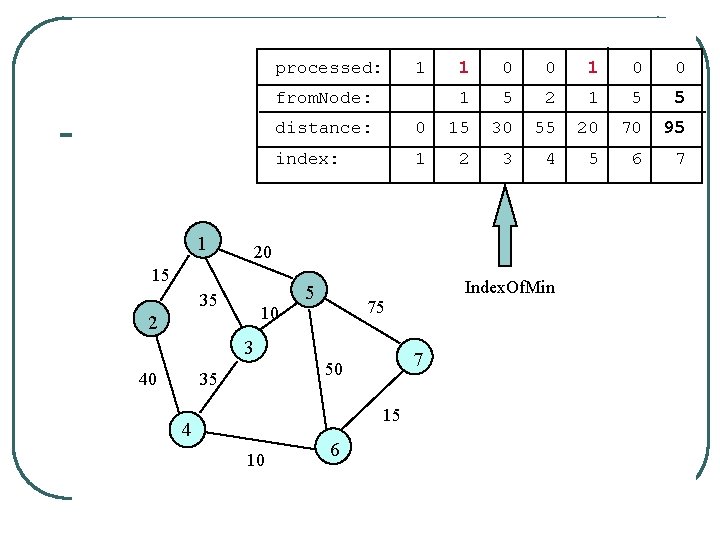
processed: 1 from. Node: 1 0 0 1 5 2 1 5 5 distance: 0 15 30 55 20 70 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 Index. Of. Min 5 75 3 40 1 7 50 35 15 4 10 6

processed: 1 from. Node: 1 1 0 0 1 5 2 1 5 5 distance: 0 15 30 55 20 70 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6 Unprocessed node adjacent to 3 is 4. 55 < 30 + 35 = 65 no change in array

processed: 1 from. Node: 1 1 0 0 1 5 2 1 5 5 distance: 0 15 30 55 20 70 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6

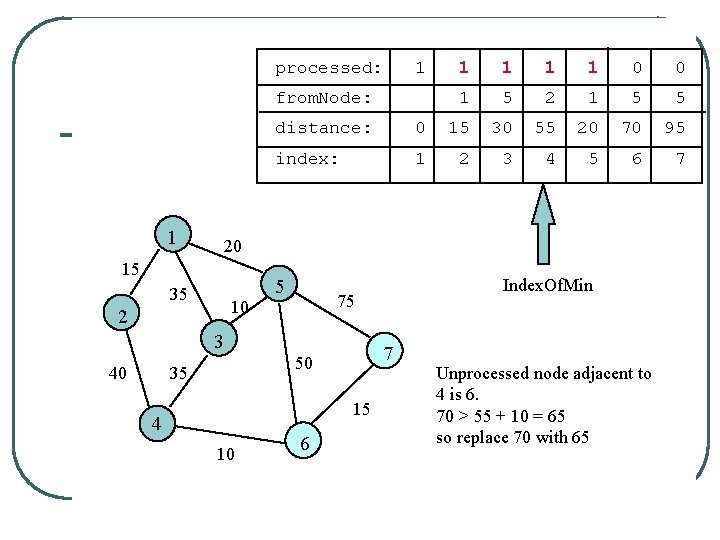
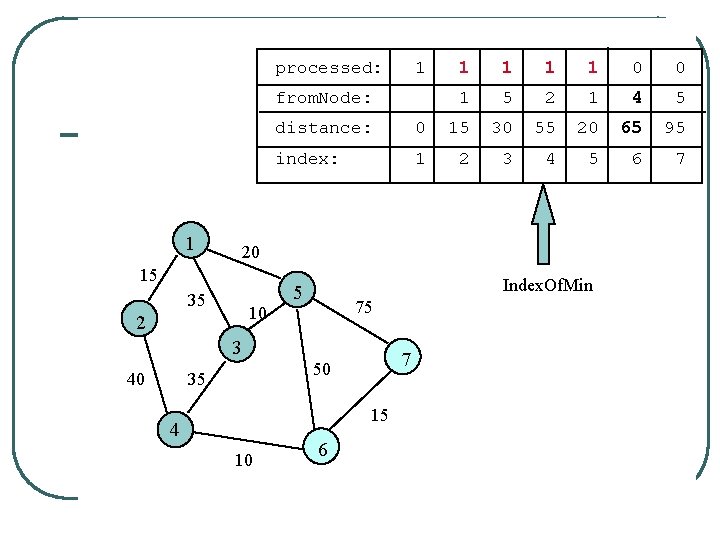
processed: 1 from. Node: 1 1 0 0 1 5 2 1 5 5 distance: 0 15 30 55 20 70 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6 Unprocessed node adjacent to 4 is 6. 70 > 55 + 10 = 65 so replace 70 with 65

processed: 1 from. Node: 1 1 0 0 1 5 2 1 4 5 distance: 0 15 30 55 20 65 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 Index. Of. Min 5 75 3 40 1 7 50 35 15 4 10 6

processed: 1 from. Node: 1 1 0 0 1 5 2 1 4 5 distance: 0 15 30 55 20 65 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6

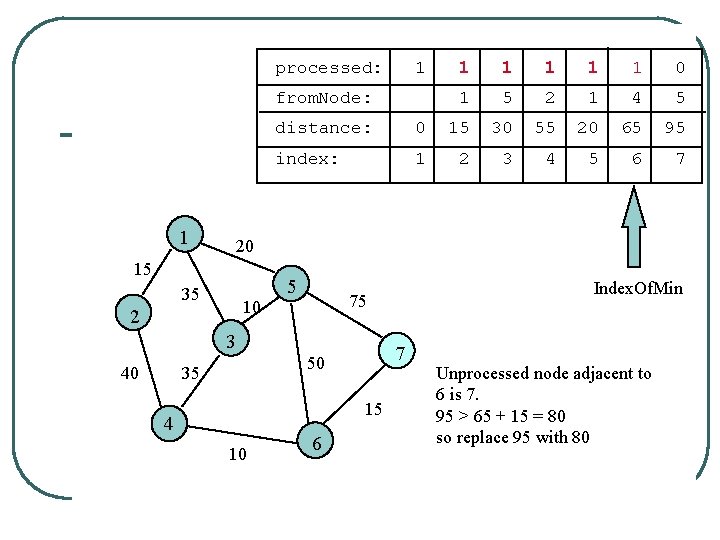
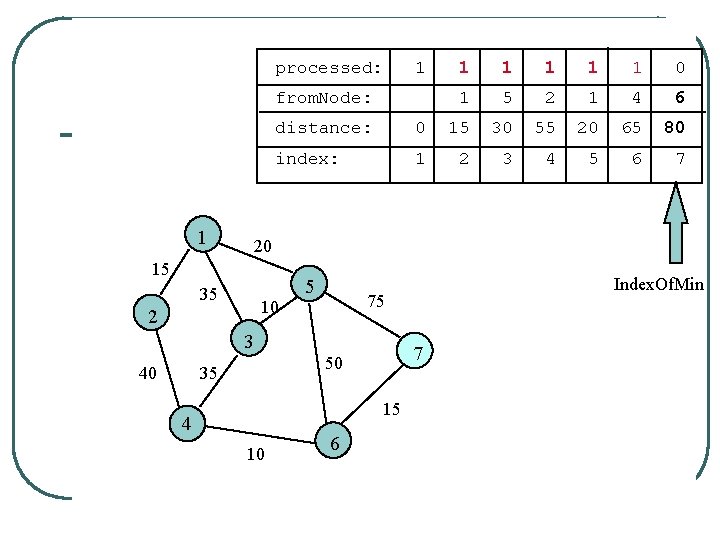
processed: 1 from. Node: 1 1 1 0 1 5 2 1 4 5 distance: 0 15 30 55 20 65 95 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6 Unprocessed node adjacent to 6 is 7. 95 > 65 + 15 = 80 so replace 95 with 80

processed: 1 from. Node: 1 1 1 0 1 5 2 1 4 6 distance: 0 15 30 55 20 65 80 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6

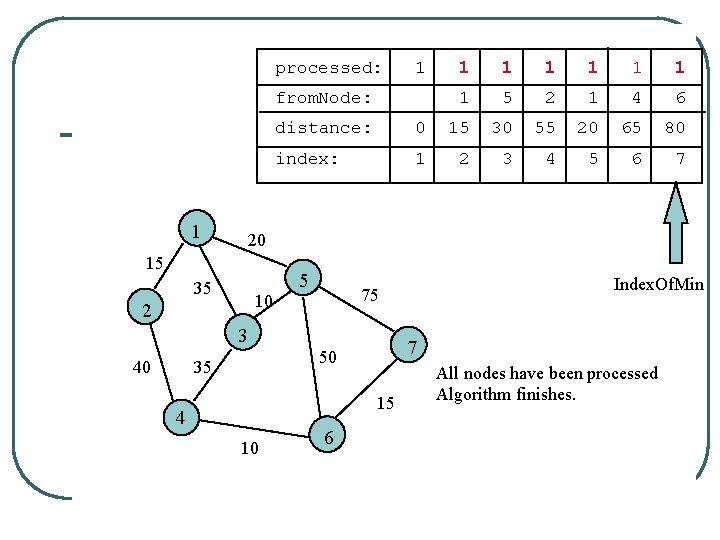
processed: 1 from. Node: 1 1 1 1 5 2 1 4 6 distance: 0 15 30 55 20 65 80 index: 1 2 3 4 5 6 7 20 15 35 10 2 5 7 50 35 15 4 10 Index. Of. Min 75 3 40 1 6 All nodes have been processed Algorithm finishes.

Theorems Dijkstra’s algorithm finds the length of a shortest path between two vertices in a connected simple undirected weighted graph. Dijkstra’s algorithm uses O(n 2) operations (additions and comparisons) to find the length of the shortest path between two vertices in a connected simple undirected weighted graph.

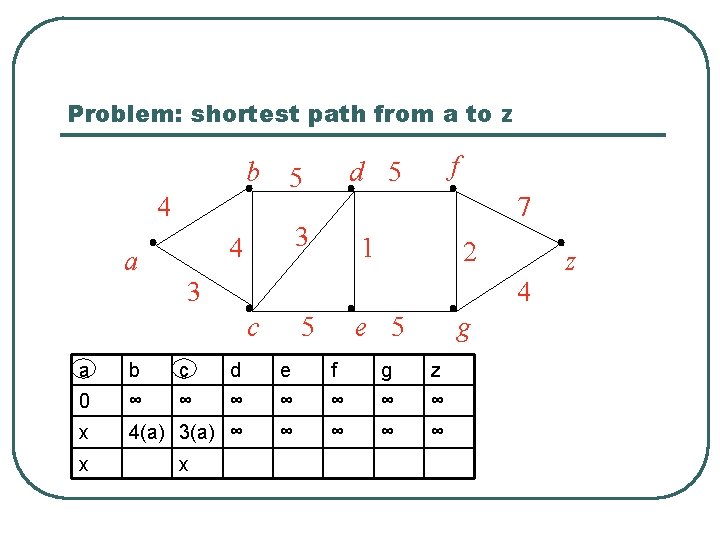
Problem: shortest path from a to z b 4 5 d 5 3 1 4 a f 7 2 3 z 4 c 5 e 5 g a b c d e f g z 0 ∞ ∞ ∞ ∞ x 4(a) 3(a) ∞ ∞ ∞ x x