Shortest Path Problems FloydWarshall Algorithm for the AllPairs

Shortest Path Problems: Floyd-Warshall Algorithm for the All-Pairs Shortest Path Problem with Arbitrary Arc Costs Updated 18 February 2008

Floyd-Warshall Algorithm (AMO pg 148) begin for all node pairs [i, j] N x N do d[i, j] : = , pred[i, j] : = 0; for all nodes i N do d[i, i] : = 0; for all arcs (i, j) A do d[i, j] : = cij and pred[i, j] : = i; for k = 1 to n do for all node pairs [i, j] N x N do if d[i, j] > d[i, k] + d[k, j] then d[i, j] : = d[i, k] + d[k, j] and pred[i, j] : = pred[k, j]; end;

Interpretation of d and pred Matrices • At the end of iteration k, d[i, j] is the length of a shortest path from i to j that uses only nodes in the set {1, 2, …, k} as internal nodes. • pred[i, j] is the node prior to node j on the (current) shortest path from i to j.

The Triangle Operation: Iteration k i k j Check if d[i, j] > d[i, k] + d[k, j]

The Triangle Operation: Update pred[i, j] k i old pred[i, j] pred[k, j] j new pred[i, j] = pred[k, j]

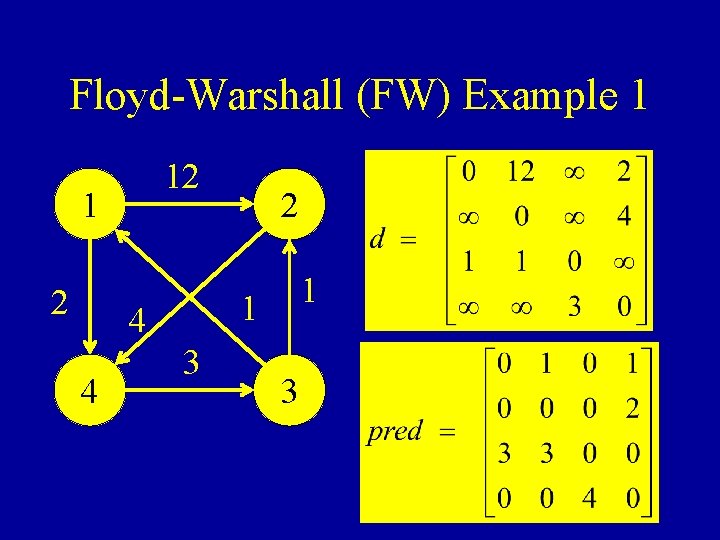
Floyd-Warshall (FW) Example 1 12 1 1 4 4 2 3 3

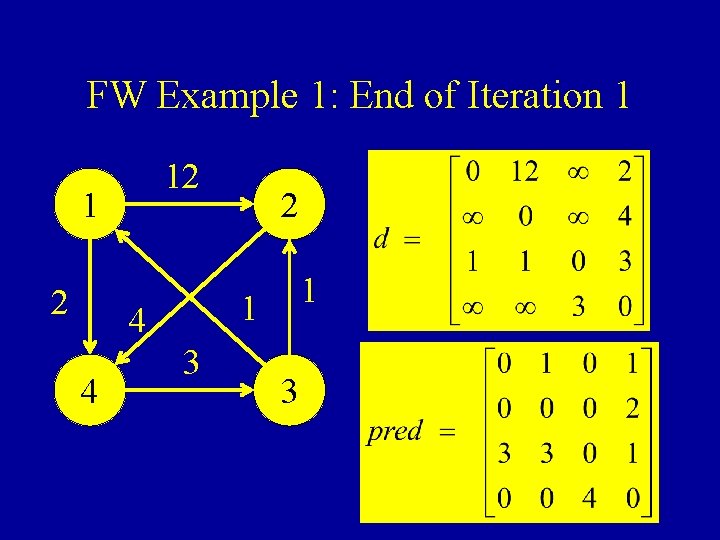
FW Example 1: End of Iteration 1 12 1 1 4 4 2 3 3

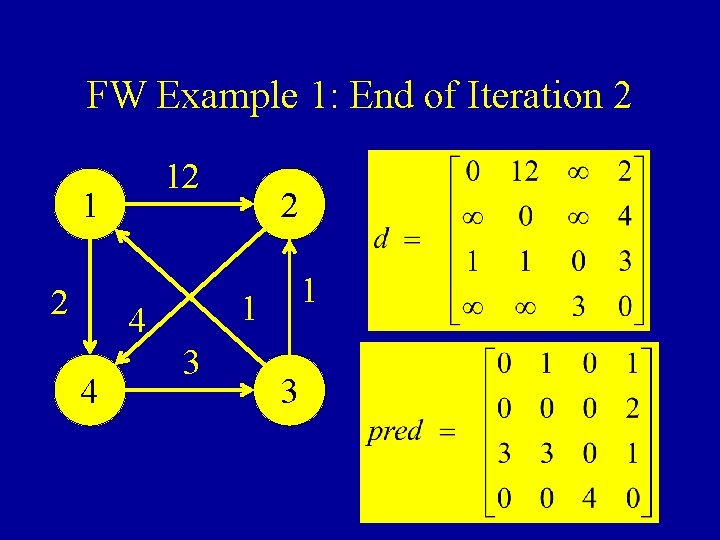
FW Example 1: End of Iteration 2 12 1 1 4 4 2 3 3

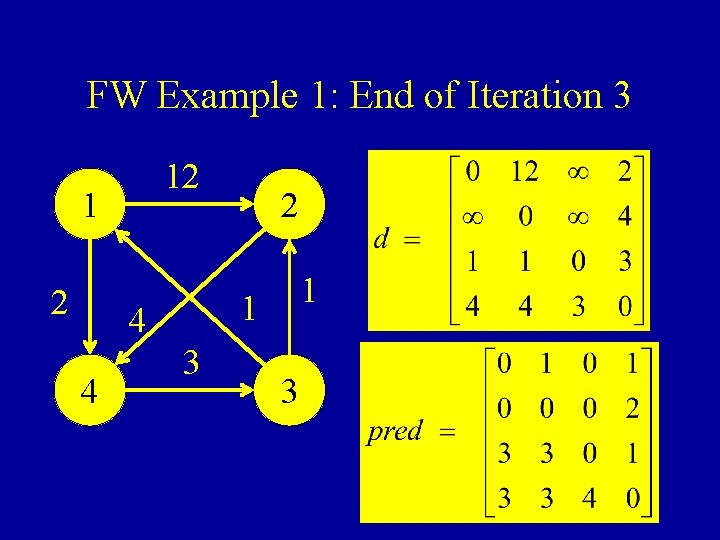
FW Example 1: End of Iteration 3 12 1 1 4 4 2 3 3

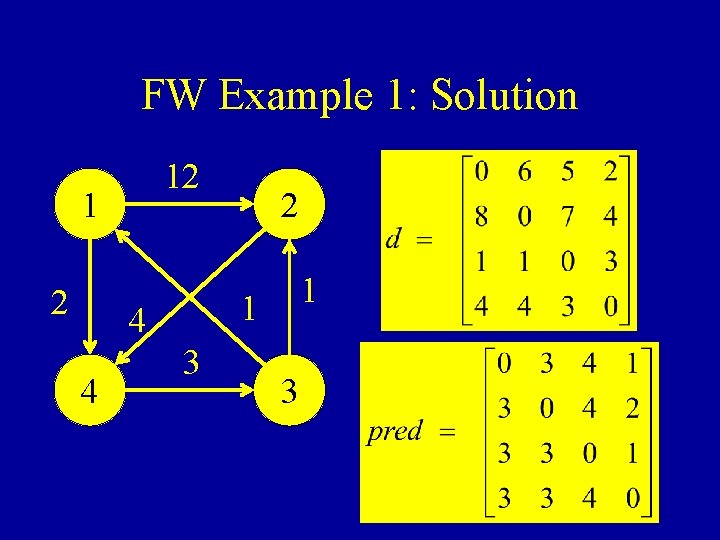
FW Example 1: Solution 12 1 1 4 4 2 3 3

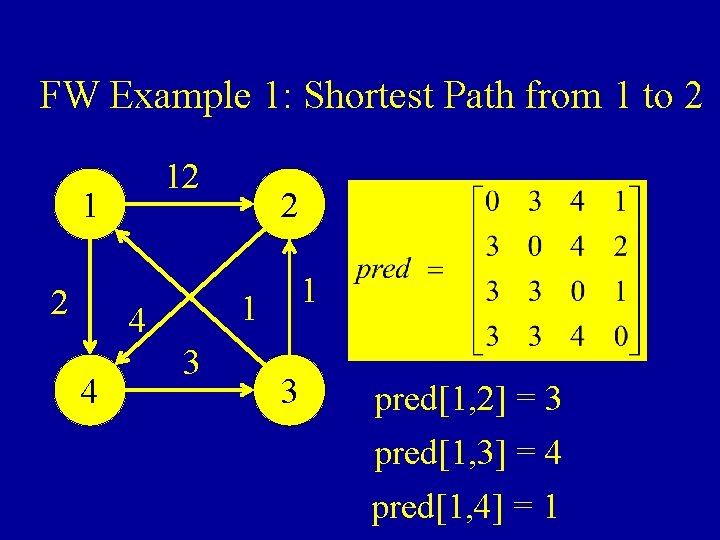
FW Example 1: Shortest Path from 1 to 2 12 1 1 4 4 2 3 3 pred[1, 2] = 3 pred[1, 3] = 4 pred[1, 4] = 1

Complexity of Floyd-Warshall • • Each triangle operation is O(1) Each iteration does n 2 triangle operations There are n iterations Complexity is O(n 3)

Testing for Negative-Cost Cycles for k = 1 to n do for all node pairs [i, j] N x N do if d[i, j] > d[i, k] + d[k, j] then begin d[i, j] : = d[i, k] + d[k, j] and pred[i, j] : = pred[k, j]; if i = j and d[i, i] < 0 then exit; (G has a negative-cost cycle) end;

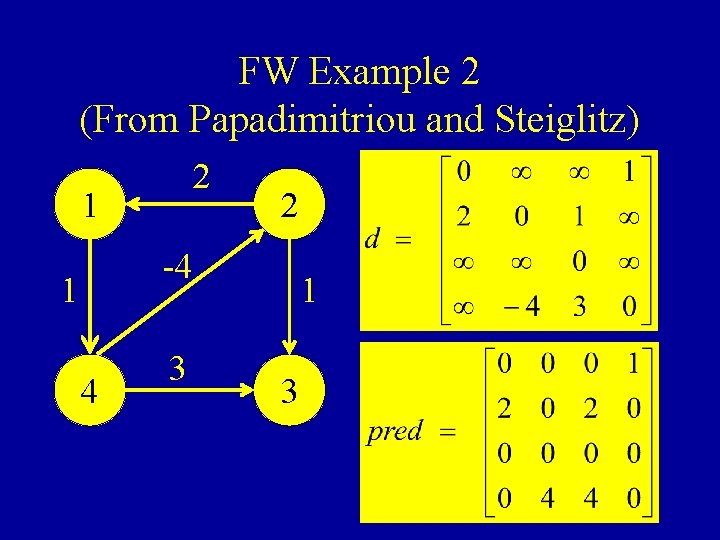
FW Example 2 (From Papadimitriou and Steiglitz) 2 1 2 -4 1 4 3 1 3

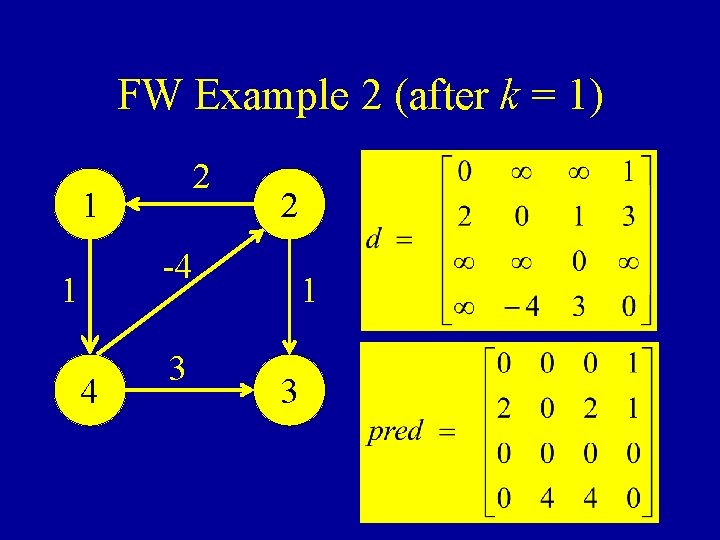
FW Example 2 (after k = 1) 2 1 2 -4 1 4 3 1 3

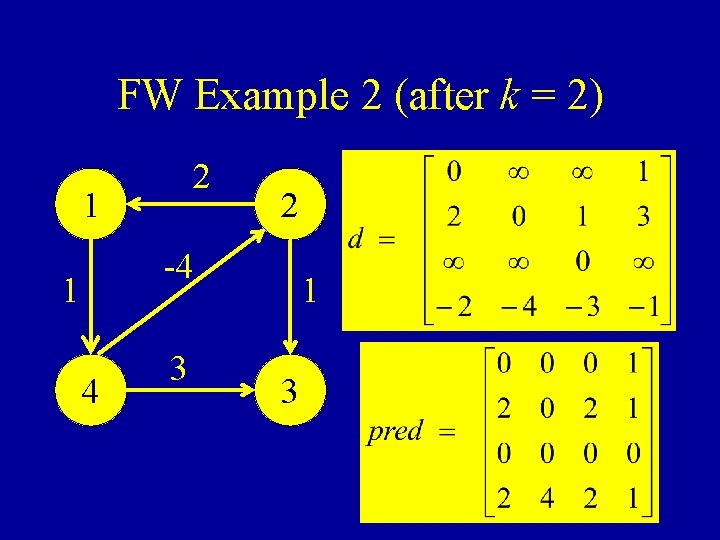
FW Example 2 (after k = 2) 2 1 2 -4 1 4 3 1 3

FW Example 2: d[4, 4] = 1 2 -4 1 4 3 1 3 pred[4, 4] = 1 pred[4, 1] = 2 pred[4, 2] = 4