Shortest Path Consider the following weighted undirected graph

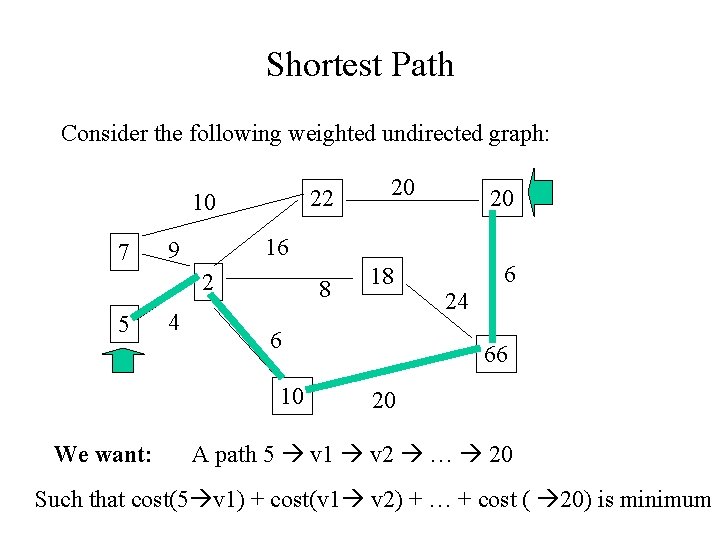
Shortest Path Consider the following weighted undirected graph: 22 10 7 4 8 18 6 10 We want: 20 16 9 2 5 20 6 24 66 20 A path 5 v 1 v 2 … 20 Such that cost(5 v 1) + cost(v 1 v 2) + … + cost ( 20) is minimum

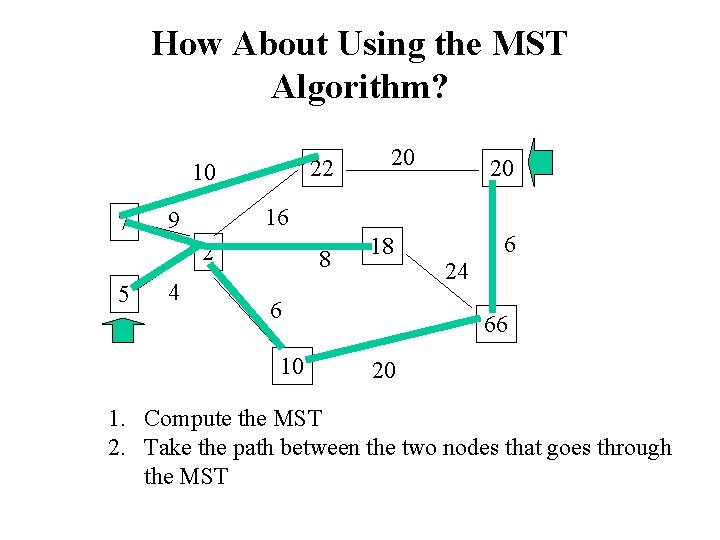
How About Using the MST Algorithm? 22 10 7 4 20 16 9 2 5 20 8 18 6 10 6 24 66 20 1. Compute the MST 2. Take the path between the two nodes that goes through the MST

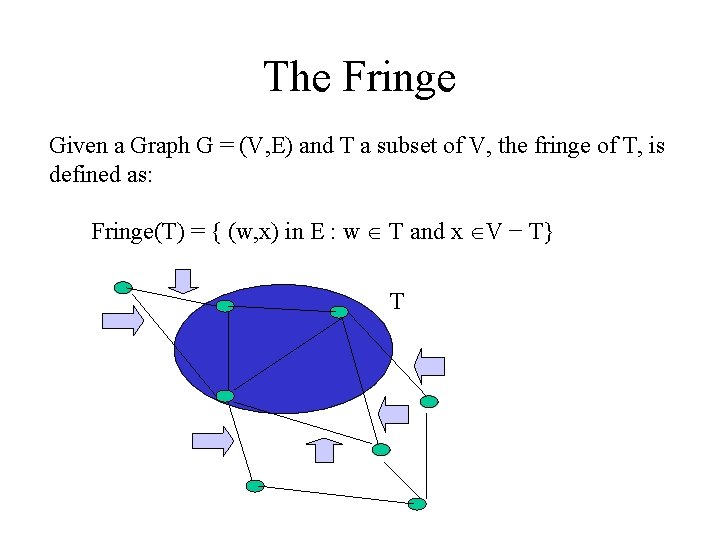
The Fringe Given a Graph G = (V, E) and T a subset of V, the fringe of T, is defined as: Fringe(T) = { (w, x) in E : w T and x V − T} T

Djikstra Algorithm: Idea • We are computing a shortest path from node u to a node v • Start the algorithm with T = {u}, construct Fringe(T) • At each iteration, select the (z, w) in Fringe(T) such that the path from u to w has the lowest cost • Stop when v is part of T (not of the fringe!)

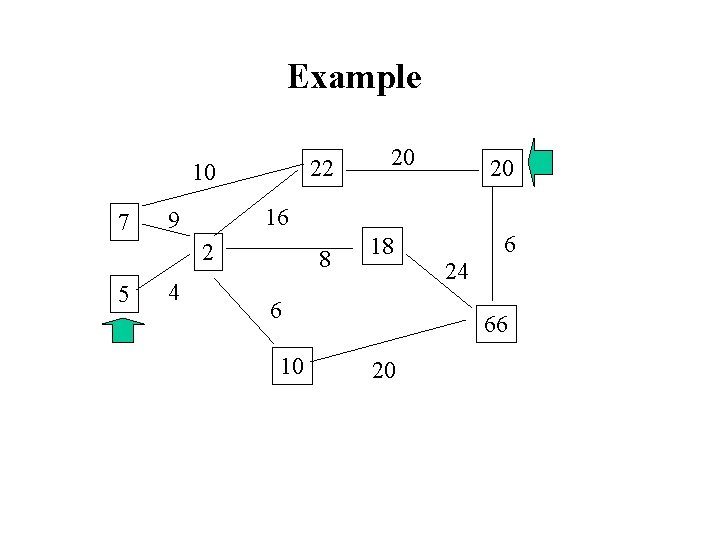
Example 22 10 7 4 20 16 9 2 5 20 8 18 6 10 6 24 66 20

The Dijkstra’s Algorithm // Input: G = (G, V), nodes u and v in V //output: Shortest path from u to v T {u}; F Fringe({u}); ET {} While v is not in the T do Choose (z, w) in F with the shortest path (u, u 1), (u 1, u 2), …, (un, z) (z, w) with (u, u 1), (u 1, u 2), …, (un, z) in ET T T {w} ET {(z, w)} for each {(w, x) : (w, x) in E − ET } do If no (w’, x) in F then F F {(w, x)} else If the path u x going through (w, x) has less weight than the path u x going through (w’, x) then F ( F − {(w’, x)}) {(w, x)}

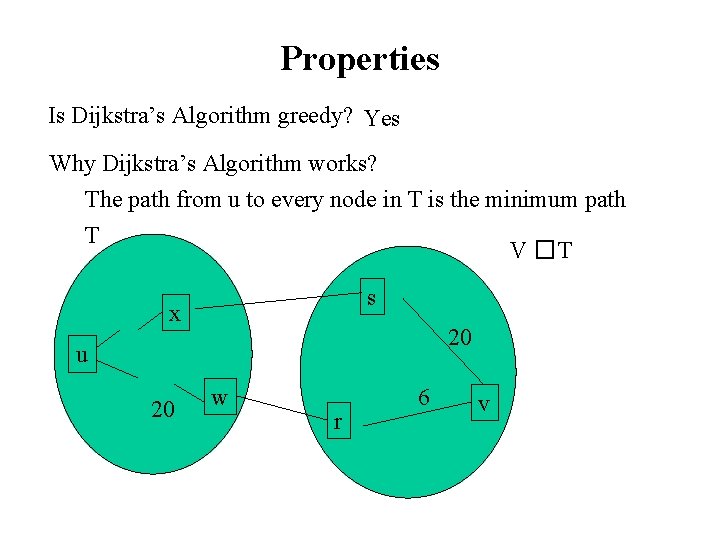
Properties Is Dijkstra’s Algorithm greedy? Yes Why Dijkstra’s Algorithm works? The path from u to every node in T is the minimum path T V �T s x 20 u 20 w r 6 v

Complexity • Actual complexity is O(|E|log 2 |E|) • It is easy to see that it is at most |E||V| (i. e. , |E|2): Ø the outer “while” is performed |V| times Ø the inner for is performed at most |E| times

• 010 1. 2. 3. 4. 5. 6. • 011 1. 2. 3. 4. 5. 6. Homework Write the pseudo-code for the algorithm inserting an element in a minheap Do the same for a Heap Write the pseudo-code for is. Leaf(i) (Slide 15 of class about Heaps) Change Dijkstra’s Algorithm (Slide 6) to compute the minimum distance from u to every node in the graph True or False: the subgraph (T, ET) resulting from 4 is an MST of the input graph In the graph of 2. b (Page 323). Follow Dijkstra’s Algorithm to compute the path from c to l Write the pseudo-code for the algorithm deleting the element with the minimum priority value in a min-heap Do the same but deleting the one with the highest priority for a Heap Write the pseudo-code for Parent(i) (Slide 15 of class about Heaps) Change Dijkstra’s Algorithm (Slide 6) to compute the minimum distance from u to every node in the graph True or False: the subgraph (T, ET) resulting from 4 is a tree connecting all nodes of the input graph In the graph of 2. b (Page 323). Follow Dijkstra’s Algorithm to compute the