Shors Factoring Algorithm David Poulin Institute for Quantum

Shor’s Factoring Algorithm David Poulin Institute for Quantum Computing & Perimeter Institute for Theoretical Physics Guelph, September 2003

Summary • Some number theory • Shor’s entire algorithm • Quantum circuits • Phase estimation • Quantum Fourier transform • Final circuit David Poulin, IQC & PI

A bit of number theory Theorem If a ±b (mod N) but a 2 b 2 (mod N) Then gcd(a+b, N) is a factor of N. Proof a 2 - b 2 0 (mod N) (a - b)(a+b) 0 (mod N) ( t) [ (a - b) (a+b) = t. N ] u. N v. N gcd(a+b, N) is a non trivial factor of N. David Poulin, IQC & PI

Shor’s entire algorithm N is to be factored: Choose random x: 2 x N-1. If gcd(x, N) 1, Bingo! Find smallest integer r : xr 1 (mod N) If r is odd, GOTO 1 If r is even, a = xr/2 (mod N) If a = N-1 GOTO 1 Easy 7. ELSE gcd(a+1, N) is a non trivial factor of N. Easy 1. Easy 2. Hard 3. Easy 4. Easy 5. Easy 6. David Poulin, IQC & PI

Success probability Theorem If N has k different prime factors, probability of success for random x is 1 - 1/2 k-1. Add this step to Shor’s algorithm: Easy 0. -Test if N=N’ 2 l and apply Shor to N’ -Compute for 2 j ln 2 N. If one of these root is integer, apply Shor to this root. Probability of success ½. David Poulin, IQC & PI

Classical computing Basic logical unit: the bit 0 or 1 Universal set: (Not-and, Swap, Copy) A A B Swap Not-and(A B) A B B A B NAND (A B) 0 0 1 1 1 0 Copy A A A David Poulin, IQC & PI

Bits and Qubits Classical 1 bit Quantum 1 qubit 0 or 1 n bits | + |1 | |2 + | |2=1 n qubits 000. . . 0 (0) 000. . . 1 (1) … 111. . . 1 (2 n-1) Measure b 1 b 2 b 3. . . bn (|4 - |7 ) = = (|0100 - |0111 ) |01 (|00 - |11 ) Measure i with probability |ci|2 David Poulin, IQC & PI

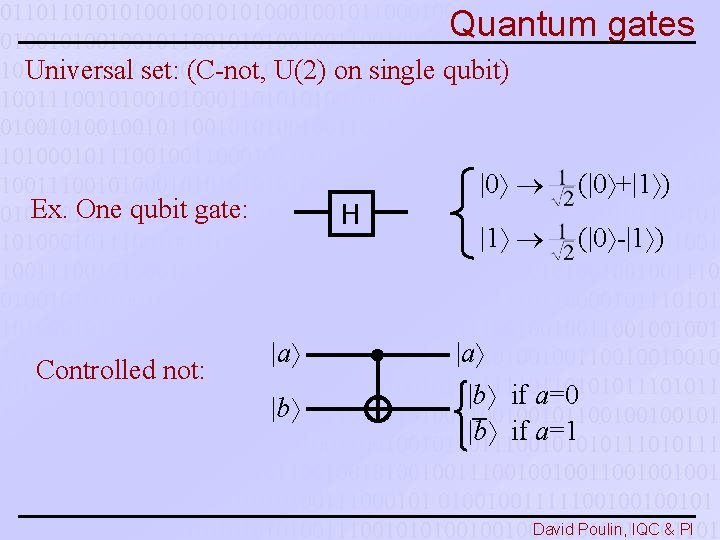
Quantum gates Universal set: (C-not, U(2) on single qubit) Ex. One qubit gate: Controlled not: H |a |b |0 (|0 +|1 ) |1 (|0 -|1 ) |a |b if a=0 |b if a=1 David Poulin, IQC & PI

Composing Quantum gates Use linearity of quantum mechanics. |0 H (|0 |0 +|1 |1 ) |0 (|0 + |1 ) |0 = (|0 |0 + |1 |0 ) Any classical computation can be made reversibly (one to one) with poly overhead. Any reversible classical computation can be performed on a quantum computer with poly overhead. David Poulin, IQC & PI

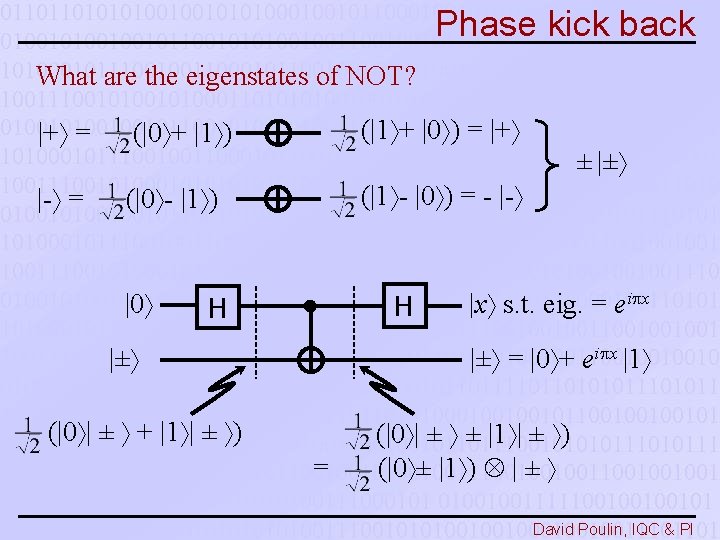
Phase kick back What are the eigenstates of NOT? |+ = (|0 + |1 ) (|1 + |0 ) = |+ |- = (|0 - |1 ) (|1 - |0 ) = - |- |0 ± |± H H |± |x s. t. eig. = ei x |± = |0 + ei x |1 (|0 | ± + |1 | ± ) = (|0 | ± ± |1 | ± ) (|0 ± |1 ) | ± David Poulin, IQC & PI

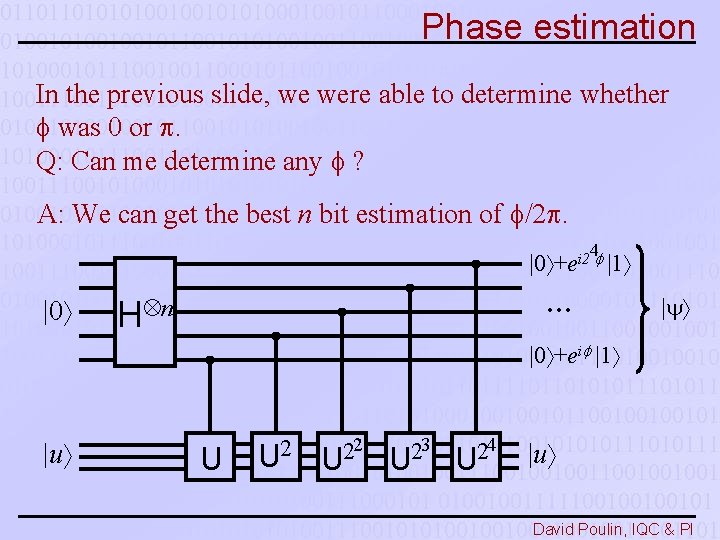
Phase estimation In the previous slide, we were able to determine whether was 0 or . Q: Can me determine any ? A: We can get the best n bit estimation of /2. 4 i 2 |0 +e |1 |0 … H n | |0 +ei |1 |u U U 2 2 2 U 3 2 U 4 2 U |u David Poulin, IQC & PI

Quantum Fourier Transform F (binary extension of x/2 n mod 1) So applying F-1 to | will yield |x that is the best n bit estimation of /2. David Poulin, IQC & PI

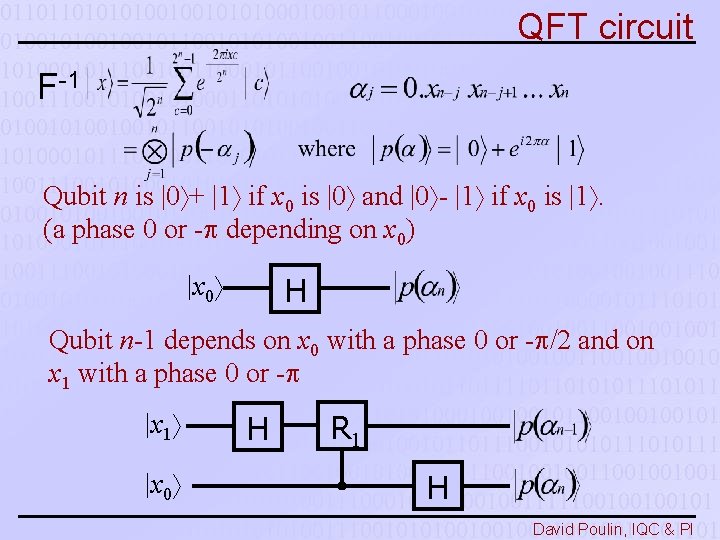
QFT circuit F-1 Qubit n is |0 + |1 if x 0 is |0 and |0 - |1 if x 0 is |1. (a phase 0 or - depending on x 0) |x 0 H Qubit n-1 depends on x 0 with a phase 0 or - /2 and on x 1 with a phase 0 or - |x 1 |x 0 H R 1 H David Poulin, IQC & PI

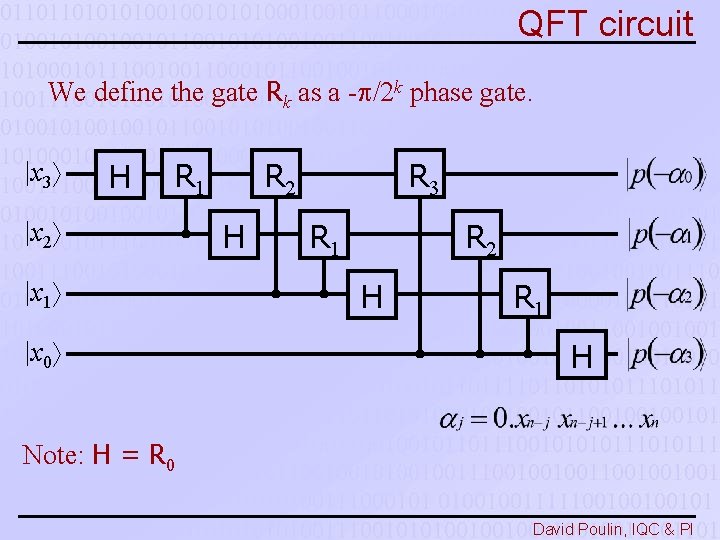
QFT circuit We define the gate Rk as a - /2 k phase gate. |x 3 H R 1 |x 2 |x 1 |x 0 R 2 H R 3 R 1 R 2 H R 1 H Note: H = R 0 David Poulin, IQC & PI

Multiplication Consider UN, a : |x |ax mod N. Then, for k = 1, . . . , r are eigenstates of UN, a with eigenvalues UN, a If we could prepare such a state, we could obtain an estimation of k/r hence of r. It requires the knowledge of r. David Poulin, IQC & PI

Multiplication Consider the sum Since The state |1 is easy to prepare. In what follows, we show that it can be used to get an estimation of k/r for random k. David Poulin, IQC & PI

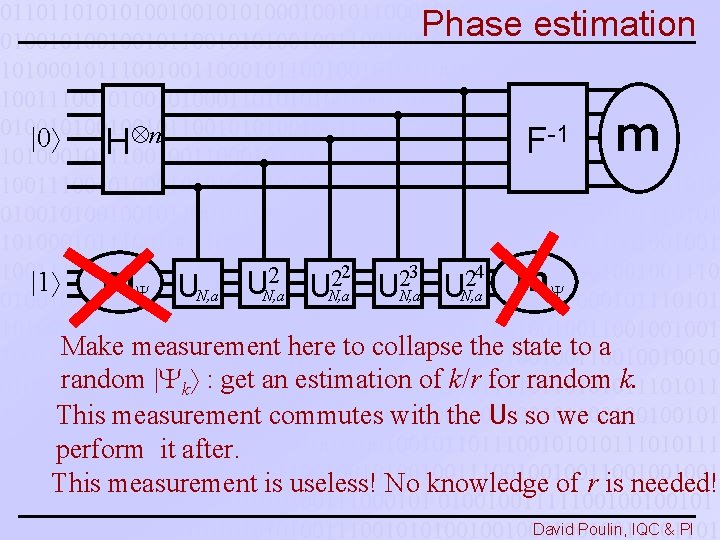
Phase estimation |0 H n |1 m F-1 UN, a U 2 N, a 2 2 U N, a 3 2 U N, a 4 2 U N, a m m Make measurement here to collapse the state to a random | k : get an estimation of k/r for random k. This measurement commutes with the Us so we can perform it after. This measurement is useless! No knowledge of r is needed! David Poulin, IQC & PI