SHM Waves Sound AP Physics I Simple Harmonic

SHM, Waves, & Sound AP Physics I

Simple Harmonic Motion n Back and forth motion that is caused by a force that is directly proportional to the displacement. The displacement centers around an equilibrium position.

Springs – Hooke’s Law One of the simplest type of simple harmonic motion is called Hooke's Law. This is primarily in reference to SPRINGS. The negative sign only tells us that “F” is what is called a RESTORING FORCE, in that it works in the OPPOSITE direction of the displacement.

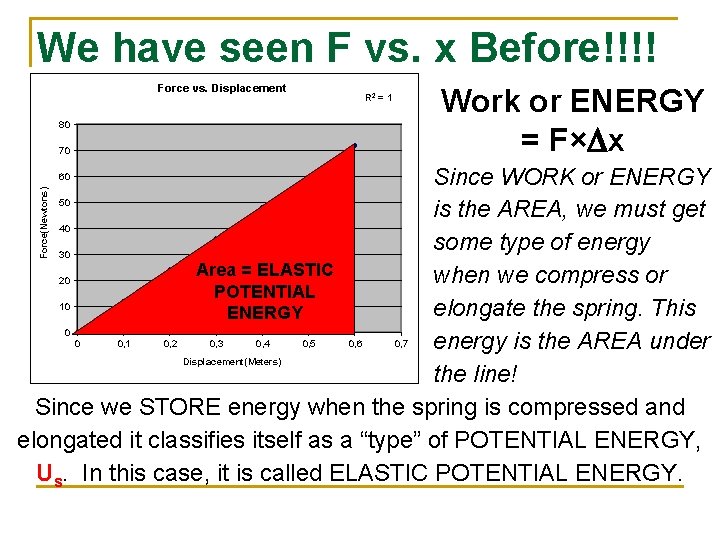
We have seen F vs. x Before!!!! Force vs. Displacement Work or ENERGY = F×Dx R 2 = 1 80 70 Since WORK or ENERGY is the AREA, we must get some type of energy Area = ELASTIC when we compress or POTENTIAL elongate the spring. This ENERGY energy is the AREA under the line! Since we STORE energy when the spring is compressed and elongated it classifies itself as a “type” of POTENTIAL ENERGY, Us. In this case, it is called ELASTIC POTENTIAL ENERGY. Force(Newtons) 60 50 40 30 20 10 0 0 0, 1 0, 2 0, 3 0, 4 Displacement(Meters) 0, 5 0, 6 0, 7

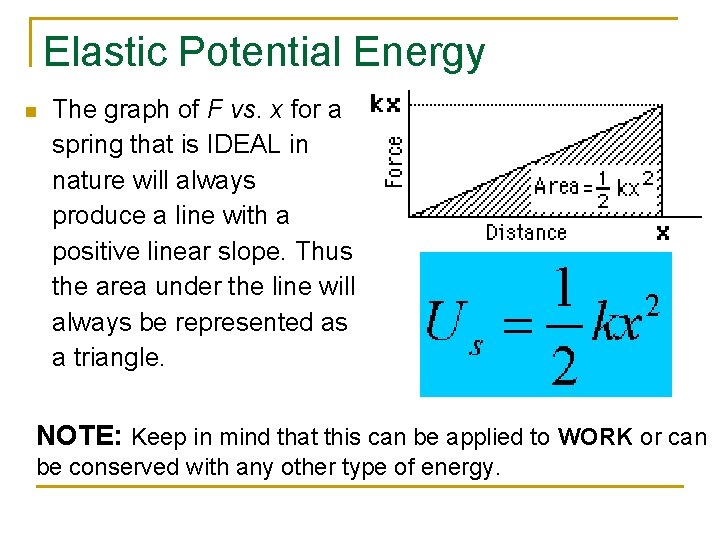
Elastic Potential Energy n The graph of F vs. x for a spring that is IDEAL in nature will always produce a line with a positive linear slope. Thus the area under the line will always be represented as a triangle. NOTE: Keep in mind that this can be applied to WORK or can be conserved with any other type of energy.

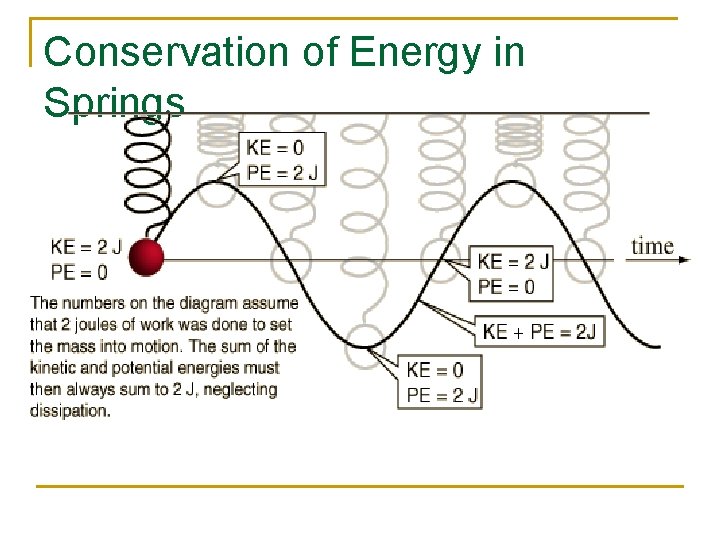
Conservation of Energy in Springs

Example A slingshot consists of a light leather cup, containing a stone, that is pulled back against 2 rubber bands. It takes a force of 30 N to stretch the bands 1. 0 cm. (a) (b) What is the potential energy stored in the bands when a 50. 0 g stone is placed in the cup and pulled back 0. 20 m from the equilibrium position? With what speed does it leave the slingshot? 3000 N/m 60 J 49 m/s

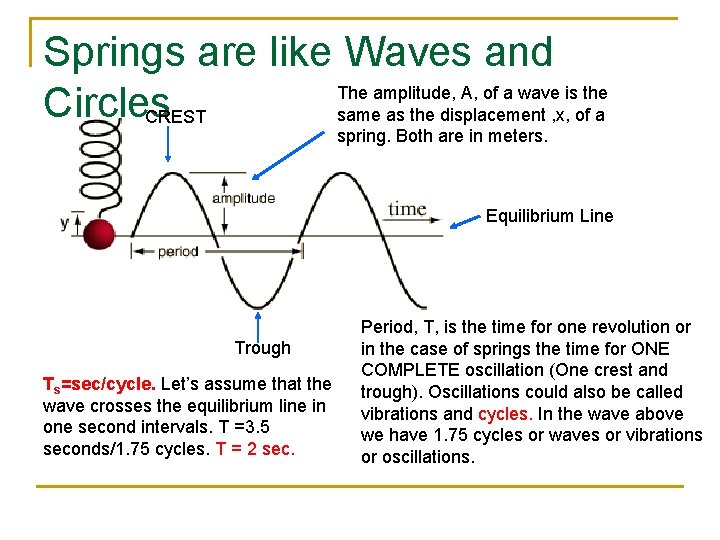
Springs are like Waves and The amplitude, A, of a wave is the Circles same as the displacement , x, of a CREST spring. Both are in meters. Equilibrium Line Trough Ts=sec/cycle. Let’s assume that the wave crosses the equilibrium line in one second intervals. T =3. 5 seconds/1. 75 cycles. T = 2 sec. Period, T, is the time for one revolution or in the case of springs the time for ONE COMPLETE oscillation (One crest and trough). Oscillations could also be called vibrations and cycles. In the wave above we have 1. 75 cycles or waves or vibrations or oscillations.

Frequency The FREQUENCY of a wave is the inverse of the PERIOD. That means that the frequency is the #cycles per sec. The commonly used unit is HERTZ(HZ).

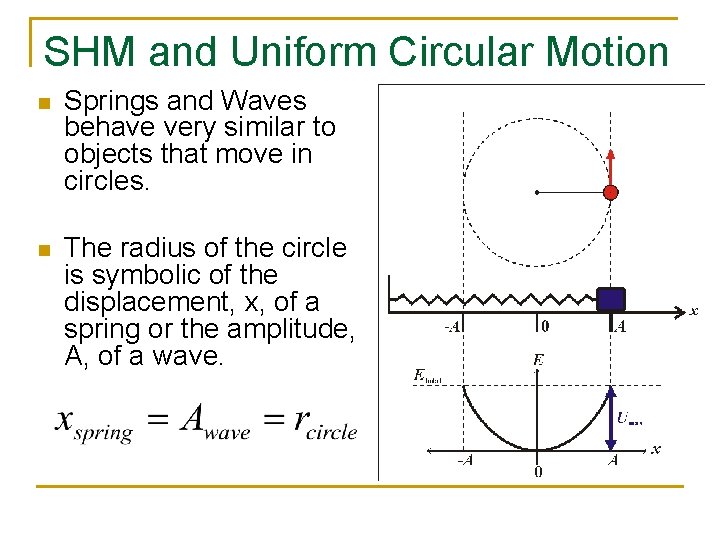
SHM and Uniform Circular Motion n Springs and Waves behave very similar to objects that move in circles. n The radius of the circle is symbolic of the displacement, x, of a spring or the amplitude, A, of a wave.

What is a wave A WAVE is a vibration or disturbance in space. n Waves transfer ENERGY but not MATTER! n A MEDIUM is the substance that all SOUND WAVES travel through and need to have in order to move.

Classifying Waves n Mechanical Waves – q q Waves that require a medium in order to travel Examples: n n Sound waves Seismic waves Water waves Electromagnetic Waves – q q Waves that travel through oscillating electrical and magnetic fields. Examples: n n Light X-Rays

Two types of Waves The first type of wave is called Longitudinal Wave - A fixed point will move parallel with the wave motion 2 areas: Compression- an area of high molecular density and pressure Rarefaction - an area of low molecular density and pressure

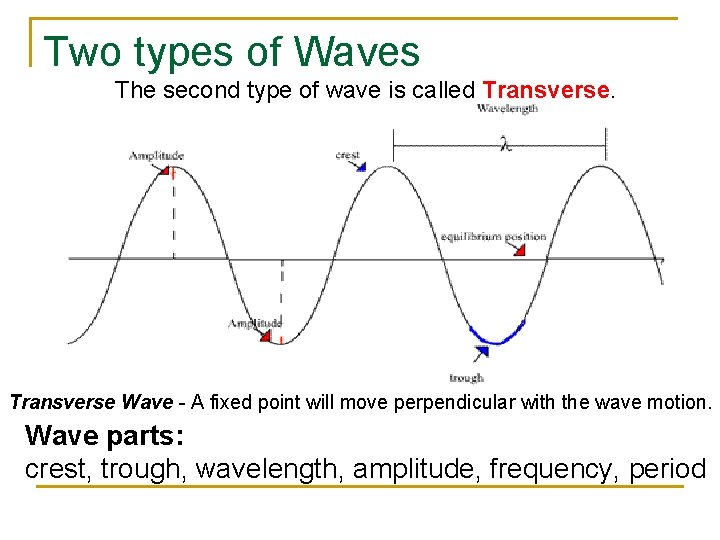
Two types of Waves The second type of wave is called Transverse Wave - A fixed point will move perpendicular with the wave motion. Wave parts: crest, trough, wavelength, amplitude, frequency, period

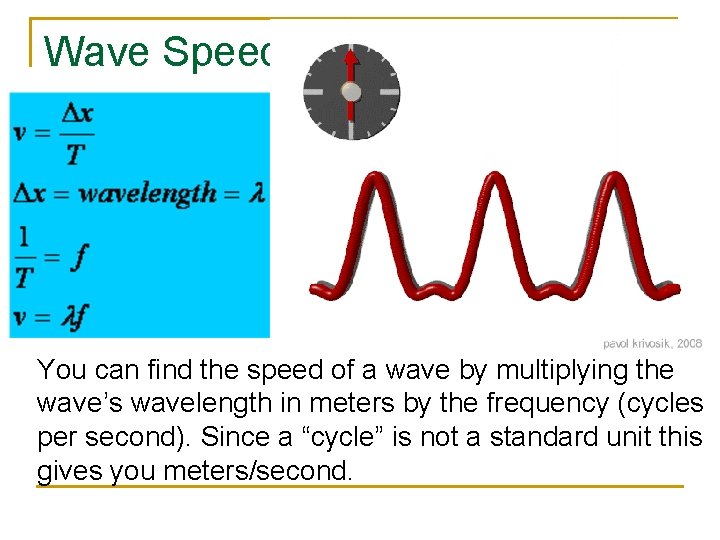
Wave Speed You can find the speed of a wave by multiplying the wave’s wavelength in meters by the frequency (cycles per second). Since a “cycle” is not a standard unit this gives you meters/second.

Example A harmonic wave is traveling along a rope. It is observed that the oscillator that generates the wave completes 40. 0 vibrations in 30. 0 s. Also, a given maximum travels 42. 5 cm along a rope in 10. 0 s. What is the wavelength? 0. 0319 m

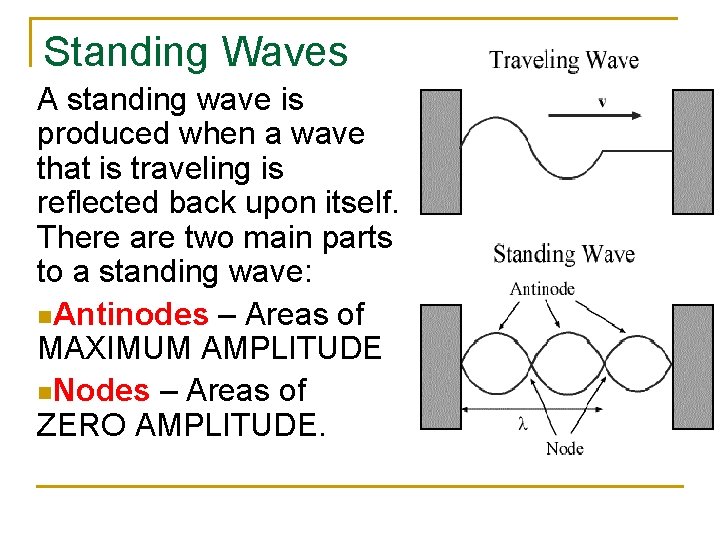
Standing Waves A standing wave is produced when a wave that is traveling is reflected back upon itself. There are two main parts to a standing wave: n. Antinodes – Areas of MAXIMUM AMPLITUDE n. Nodes – Areas of ZERO AMPLITUDE.

Sound Waves n n Sound Waves are a common type of standing wave as they are caused by RESONANCE. Resonance – when a FORCED vibration matches an object’s natural frequency thus producing vibration, sound, or even damage. One example of this involves shattering a wine glass by hitting a musical note that is on the same frequency as the natural frequency of the glass. (Natural frequency depends on the size, shape, and composition of the object in question. ) Because the frequencies resonate, or are in sync with one another, maximum energy transfer is possible.

Sound Waves n n The production of sound involves setting up a wave in air. To set up a CONTINUOUS sound you will need to set a standing wave pattern. Three LARGE CLASSES of instruments q q q n Stringed - standing wave is set up in a tightly stretched string Percussion - standing wave is produced by the vibration of solid objects Wind - standing wave is set up in a column of air that is either OPEN or CLOSED Factors that influence the speed of sound are density of solids or liquid, and TEMPERATURE

Closed Pipes Have an antinode at one end a node at the other. Each sound you hear will occur when an antinode appears at the top of the pipe. What is the SMALLEST length of pipe you can have to hear a sound? You get your first sound or encounter your first antinode when the length of the actual pipe is equal to a quarter of a wavelength. This FIRST SOUND is called the FUNDAMENTAL FREQUENCY or the FIRST HARMONIC.

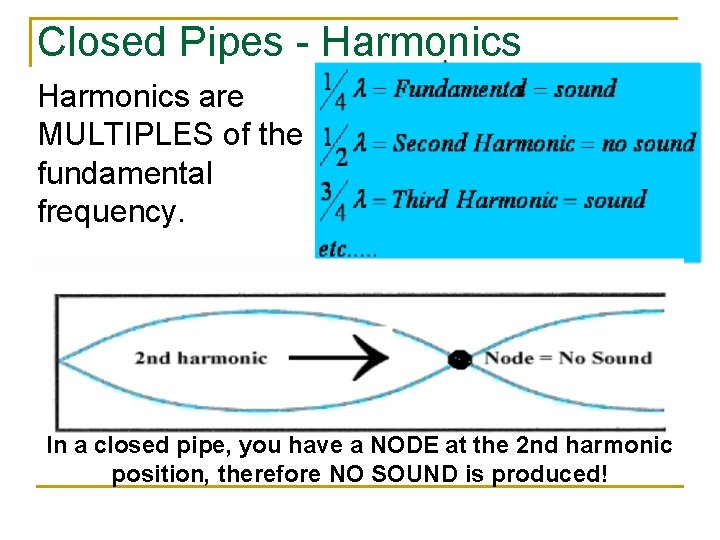
Closed Pipes - Harmonics are MULTIPLES of the fundamental frequency. In a closed pipe, you have a NODE at the 2 nd harmonic position, therefore NO SOUND is produced!

Closed Pipes - Harmonics n n In a closed pipe you have an ANTINODE at the 3 rd harmonic position, therefore SOUND is produced. CONCLUSION: Sounds in CLOSED pipes are produced ONLY at ODD HARMONICS!

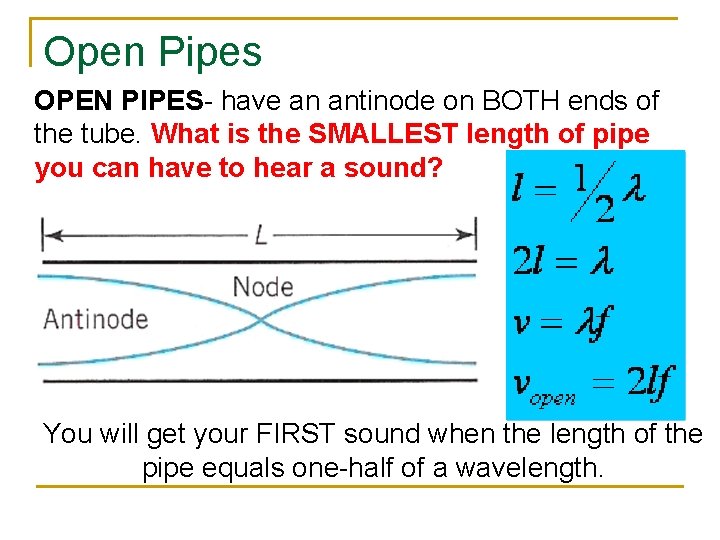
Open Pipes OPEN PIPES- have an antinode on BOTH ends of the tube. What is the SMALLEST length of pipe you can have to hear a sound? You will get your FIRST sound when the length of the pipe equals one-half of a wavelength.

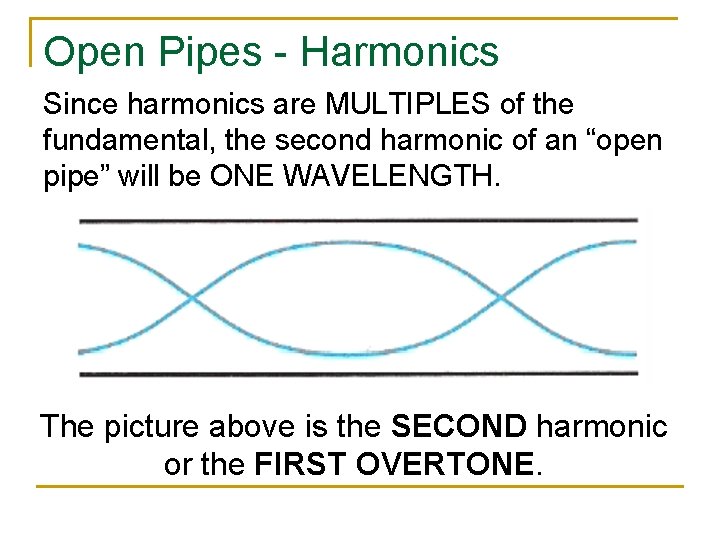
Open Pipes - Harmonics Since harmonics are MULTIPLES of the fundamental, the second harmonic of an “open pipe” will be ONE WAVELENGTH. The picture above is the SECOND harmonic or the FIRST OVERTONE.

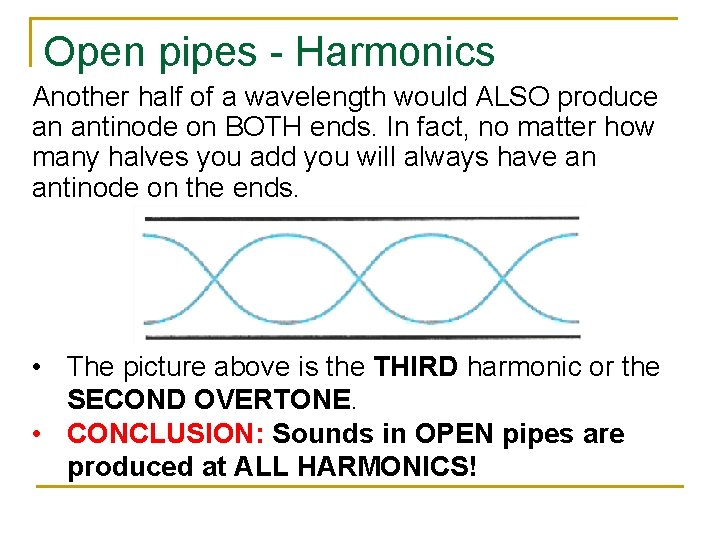
Open pipes - Harmonics Another half of a wavelength would ALSO produce an antinode on BOTH ends. In fact, no matter how many halves you add you will always have an antinode on the ends. • The picture above is the THIRD harmonic or the SECOND OVERTONE. • CONCLUSION: Sounds in OPEN pipes are produced at ALL HARMONICS!

Example The speed of sound waves in air is found to be 340 m/s. Determine the fundamental frequency (1 st harmonic) of an open-end air column which has a length of 67. 5 cm. 251. 85 HZ

Example The windpipe of a typical whooping crane is about 1. 525 -m long. What is the lowest resonant frequency of this pipe assuming it is a pipe closed at one end? Assume a temperature of 37°C. 353. 2 m/s 57. 90 Hz