Shifting Reflecting and Stretching Graphs Skill 04 Objectives

Shifting, Reflecting, and Stretching Graphs Skill 04

Objectives… • Recognize graphs of parent functions. • Use vertical and horizontal shifts and reflections to graph functions. • Use non-rigid transformations to graph functions.

Summary of Graphs of Parent Functions… One of the goals of math is to enable you to build your intuition for the basic shapes of the graphs of different types of functions without a calculator. Many functions have graphs that are simple transformations of the graphs of parent functions.

Vertical and Horizontal Shifts… Parent Function: Vertical shift two units up. Function Notation:
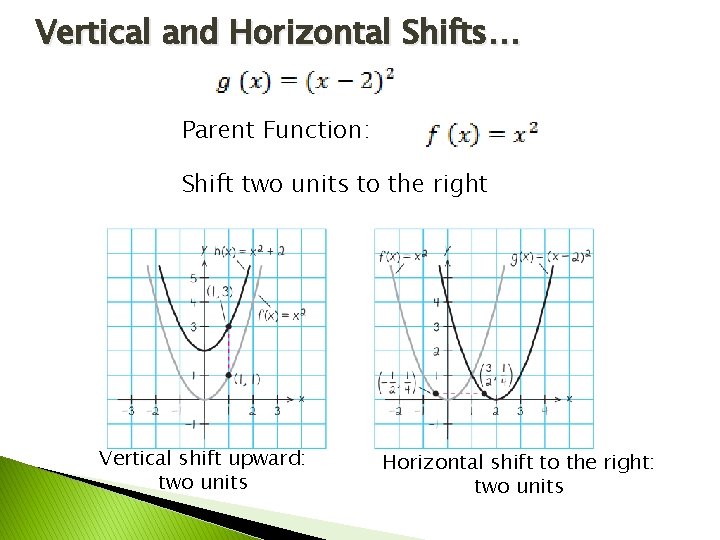
Vertical and Horizontal Shifts… Parent Function: Shift two units to the right Vertical shift upward: two units Horizontal shift to the right: two units

Vertical and Horizontal Shifts… If we assume c is a positive real number we can shift the graph of y=f(x) horizontally or vertically Vertical Shift c units up: Vertical Shift c units down: Horizontal Shift c units right: Horizontal Shift c units left:
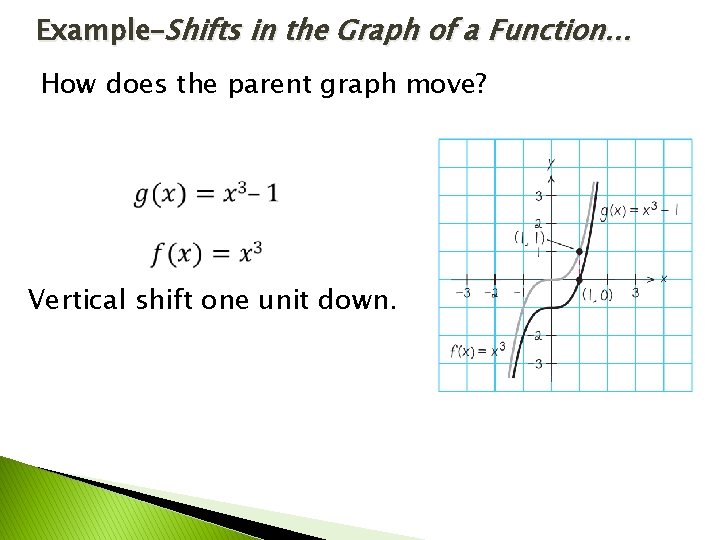
Example–Shifts in the Graph of a Function… How does the parent graph move? Vertical shift one unit down.
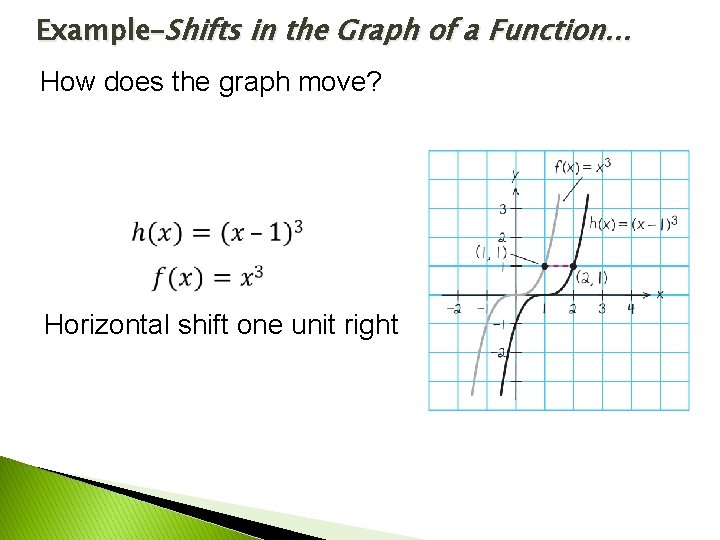
Example–Shifts in the Graph of a Function… How does the graph move? Horizontal shift one unit right

Example–Shifts in the Graph of a Function… How does the graph move? Horizontal shift two units left Vertical shift one unit up
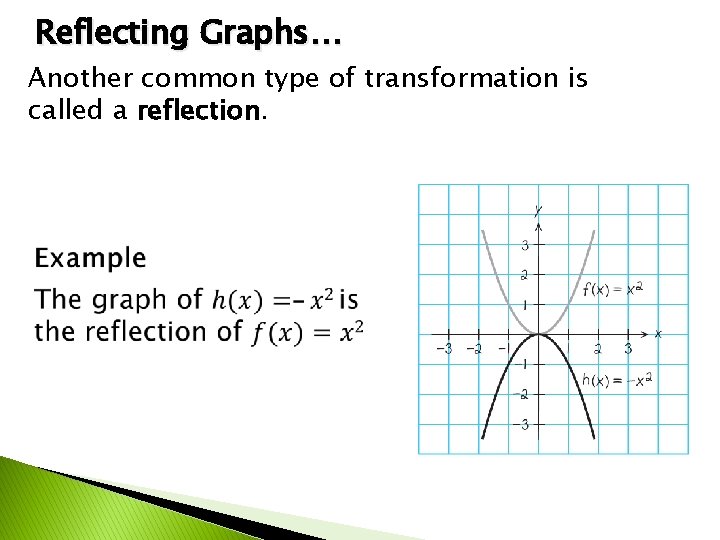
Reflecting Graphs… Another common type of transformation is called a reflection.

Reflecting Graphs… Reflection in the x-axis: Reflection in the y-axis:
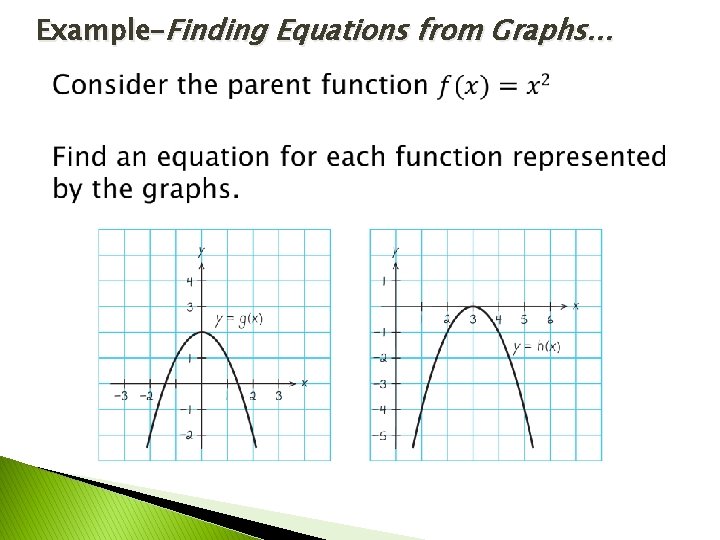
Example–Finding Equations from Graphs…
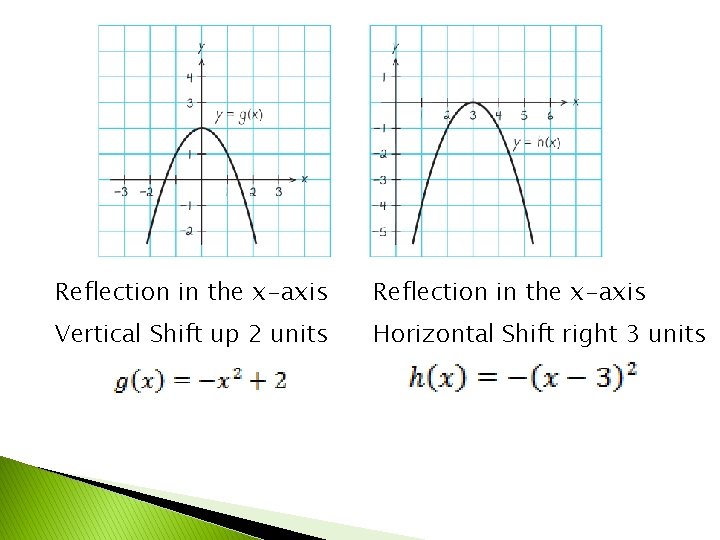
Reflection in the x-axis Vertical Shift up 2 units Horizontal Shift right 3 units

Non-rigid Transformations… Horizontal shifts, vertical shifts, and reflections are called rigid transformations because the basic shape of the graph is unchanged. These transformations change only the position of the graph in the coordinate plane. Non-rigid transformations are those that cause a distortion–a change in the shape of the original graph.

Nonrigid Transformations Vertical Stretch: Vertical Shrink: Horizontal Stretch:

Example–Non-rigid Transformations… Compare the graph of each function with the graph Solution: Vertical Stretch (all y values multiplied by 3)
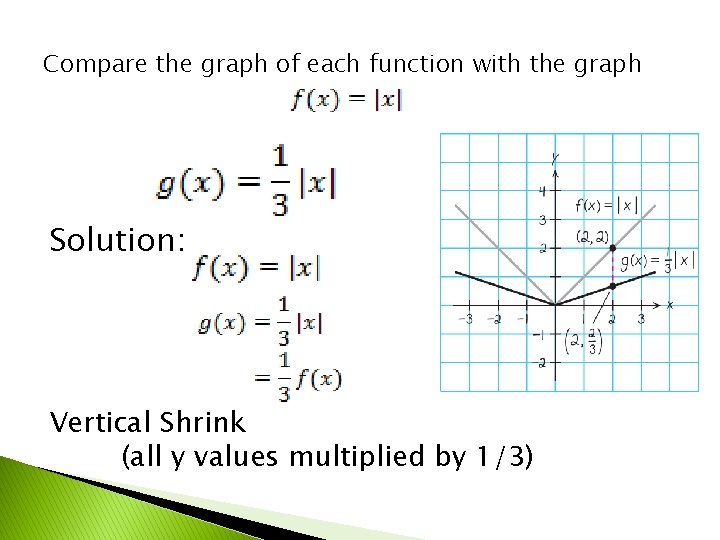
Compare the graph of each function with the graph Solution: Vertical Shrink (all y values multiplied by 1/3)

Skill 4; Shifting, Reflecting, & Stretching Graphs � Summarize � Questions? � Homework ◦ Worksheet Notes
- Slides: 18