Shellsort Review Insertion sort The outer loop of

Shellsort

Review: Insertion sort • The outer loop of insertion sort is: for (outer = 1; outer < a. length; outer++) {. . . } • The invariant is that all the elements to the left of outer are sorted with respect to one another – For all i < outer, j < outer, if i < j then a[i] <= a[j] – This does not mean they are all in their final correct place; the remaining array elements may need to be inserted – When we increase outer, a[outer-1] becomes to its left; we must keep the invariant true by inserting a[outer-1] into its proper place – This means: • Finding the element’s proper place • Making room for the inserted element (by shifting over other elements) • Inserting the element

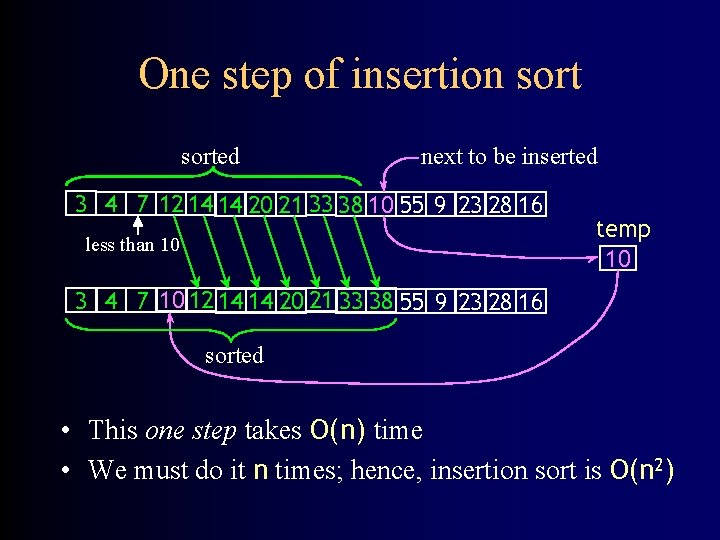
One step of insertion sorted next to be inserted 3 4 7 12 14 14 20 21 33 38 10 55 9 23 28 16 less than 10 temp 10 3 4 7 10 12 14 14 20 21 33 38 55 9 23 28 16 sorted • This one step takes O(n) time • We must do it n times; hence, insertion sort is O(n 2)

The idea of shellsort • With insertion sort, each time we insert an element, other elements get nudged one step closer to where they ought to be • What if we could move elements a much longer distance each time? • We could move each element: – A long distance – A somewhat shorter distance – A shorter distance still • This approach is what makes shellsort so much faster than insertion sort

Sorting nonconsecutive subarrays • Here is an array to be sorted (numbers aren’t important) • Consider just the red locations • Suppose we do an insertion sort on just these numbers, as if they were the only ones in the array? • Now consider just the yellow locations • We do an insertion sort on just these numbers • Now do the same for each additional group of numbers • The resultant array is sorted within groups, but not overall

Doing the 1 -sort • In the previous slide, we compared numbers that were spaced every 5 locations – This is a 5 -sort • Ordinary insertion sort is just like this, only the numbers are spaced 1 apart – We can think of this as a 1 -sort • Suppose, after doing the 5 -sort, we do a 1 -sort? – In general, we would expect that each insertion would involve moving fewer numbers out of the way – The array would end up completely sorted

Diminishing gaps • For a large array, we don’t want to do a 5 -sort; we want to do an N-sort, where N depends on the size of the array – N is called the gap size, or interval size • We may want to do several stages, reducing the gap size each time – For example, on a 1000 -element array, we may want to do a 364 -sort, then a 121 -sort, then a 40 -sort, then a 13 -sort, then a 4 -sort, then a 1 -sort – Why these numbers?

The Knuth gap sequence • No one knows the optimal sequence of diminishing gaps • This sequence is attributed to Donald E. Knuth: – Start with h = 1 – Repeatedly compute h = 3*h + 1 • 1, 4, 13, 40, 121, 364, 1093 – Stop when h is larger than the size of the array and use as the first gap, the previous number (364) – To get successive gap sizes, apply the inverse formula: h = (h – 1) / 3 • This sequence seems to work very well • It turns out that just cutting the array size in half each time does not work out as well

Analysis I • You cut the size of the array by some fixed amount, n, each time • Consequently, you have about log n stages • Each stage takes O(n) time • Hence, the algorithm takes O(n log n) time • Right? • Wrong! This analysis assumes that each stage actually moves elements closer to where they ought to be, by a fairly large amount • What if all the red cells, for instance, contain the largest numbers in the array? – None of them get much closer to where they should be • In fact, if we just cut the array size in half each time, sometimes we get O(n 2) behavior!

Analysis II • So what is the real running time of shellsort? • Nobody knows! • Experiments suggest something like O(n 3/2) or O(n 7/6) • Analysis isn’t always easy!

The End