Shell Model approach for twoproton radioactivity Nicolas Michel

Shell Model approach for two-proton radioactivity Nicolas Michel (CEA / IRFU / SPh. N) Marek Ploszajczak (GANIL) Jimmy Rotureau (ORNL – University of Tennessee) Witek Nazarewicz (ORNL – University of Tennessee) October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel

Plan • • • Experimental data R-matrix for diproton emission Shell Model Embedded in the Continuum (SMEC) SMEC with one and two particles in the continuum Used approximations for diproton emission and results Gamow Shell Model with valence protons Berggren completeness relation and Coulomb interaction Mirror effects in 6 He and 6 Be : spectroscopic factors Conclusion et perspectives October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 2

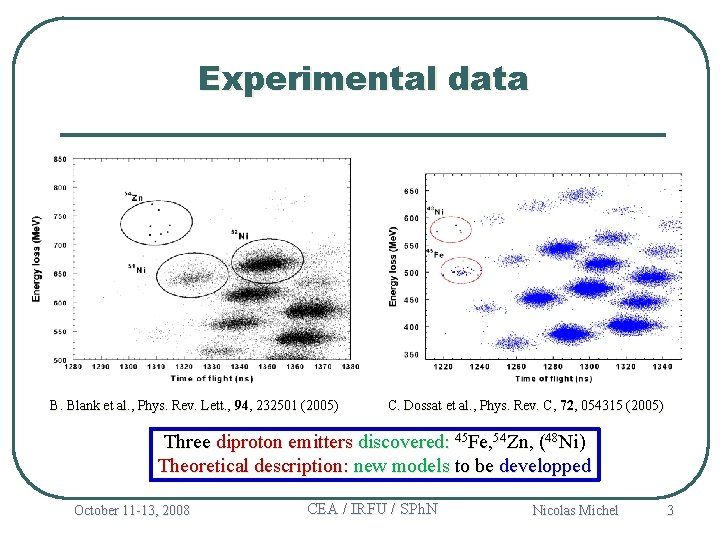
Experimental data B. Blank et al. , Phys. Rev. Lett. , 94, 232501 (2005) C. Dossat et al. , Phys. Rev. C, 72, 054315 (2005) Three diproton emitters discovered: 45 Fe, 54 Zn, (48 Ni) Theoretical description: new models to be developped October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 3

R-matrix formulation • Extension of R-matrix standard formulas: Q, P, S: available energy, penetration and shift factors ½(U): density of p+p states from s-wave phase shifts M, a, µsp 2 : reduced mass, channel radius, single particle reduced width • • • Standard Shell Model: spectroscopic factors only R-matrix reaction formulas: single particle fit, s-wave phase shifts (p+p) No mixing between channels: no continuum coupling (A. Brown, F. C. Barker, Phys. Rev. C 67, 041304(R) (2003)) October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 4

SMEC: one particle in the continuum • Feshbach space separation: Q: A bound and quasi-bound (narrow resonant) one-body states P: A-1 bound and quasi-bound one-body states, 1 scattering state (K. Bennaceur, N. Michel, F. Nowacki, J. Okolowicz and M. Ploszajczak, Phys. Lett. B, 488, 75 (2000)) (J. Okolowicz, M. Ploszajczak, and I. Rotter, Phys. Rep. , 374, , 271 (2003)) )) 374 (2003 • Hamiltonian, wave functions: October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 5

SMEC: two particles in the continuum • Two-body clusters added: Q: A bound and resonant one-body states P: A-1 bound and resonant one-body states, 1 scattering state T: A-2 bound and resonant one-body states, 2 scattering states (J. Rotureau, J. Okolowicz and M. Ploszajczak, Phys. Rev. Lett. , 95, 042503 (2005) ; Nucl. Phys. A, 767, 13 (2006)) • Approximations necessary: Full problem currently impossible to treat (zero-range interaction divergence) • Cluster emission: diproton considered as a closed system • Sequential emission: Two independent protons emitted, two-body decays system resonant: standard sequential emission system scattering: virtual sequential emission October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 6

SMEC: cluster approximation • Effective Hamiltonian: HPT and HTP couplings neglected • Two-body cluster treatment: Internal diproton degrees of freedom: phenomenological Integration over energy of cluster U, weighted by p+p s-wave density of states ½(U) Effective two-body reaction October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 7

SMEC: sequential decay • Effective Hamiltonian: HQT and HTQ couplings neglected • Two independent decays: h: mean field of the first emitted proton on the A-1 daughter nucleus Q’, P’ : subspaces associated to system All interactions between the emitted protons averaged or suppressed October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 8

SMEC: diproton decay • Q space: 1 s 0 d 0 f 1 p • Interaction in Q space: USD, KB 3, G-matrix • Interaction in P space: October 11 -13, 2008 B. Blank, M. Ploszajczak, to be published CEA / IRFU / SPh. N Nicolas Michel 9

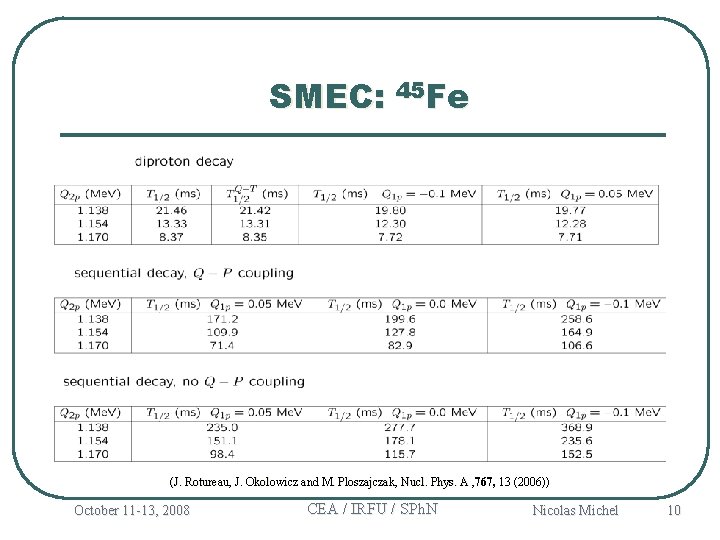
SMEC: 45 Fe (J. Rotureau, J. Okolowicz and M. Ploszajczak, Nucl. Phys. A , 767, 13 (2006)) October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 10

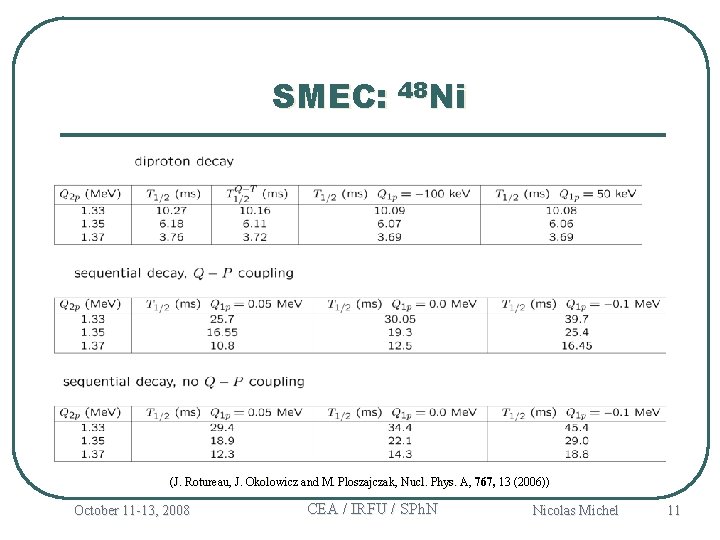
SMEC: 48 Ni (J. Rotureau, J. Okolowicz and M. Ploszajczak, Nucl. Phys. A, 767, 13 (2006)) October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 11

Gamow states • Georg Gamow : simple model for a decay G. A. Gamow, Zs f. Phys. 51 (1928) 204; 52 (1928) 510 • Definition : • Straightforward generalization to non-local potentials (HF) October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 12

Complex scaling • Calculation of radial integrals: exterior complex scaling • Analytic continuation : integral independent of R and θ October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 13

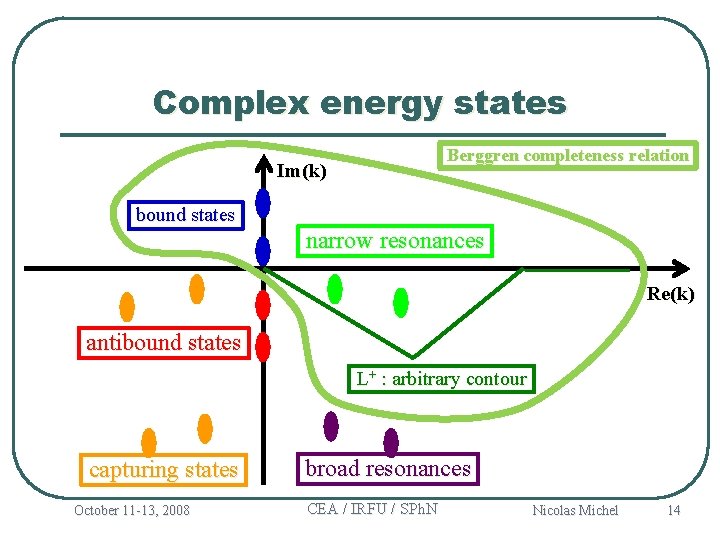
Complex energy states Berggren completeness relation Im(k) bound states narrow resonances Re(k) antibound states L+ : arbitrary contour capturing states October 11 -13, 2008 broad resonances CEA / IRFU / SPh. N Nicolas Michel 14

Completeness relation with Gamow states • Berggren completeness relation (l, j) : T. Berggren, Nucl. Phys. A 109, (1967) 205 (neutrons only) Extended to proton case (N. Michel, J. Math. Phys. , 49, 022109 (2008)) • Continuum discretization: • N-body completeness relation: October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 15

Model for 6 He and 6 Be • 6 He, 6 Be: • 6 Be: valence particles, 4 He core : Hn = T + WS(5 He) + SGI Hp = T + WS(5 Li) + SGI + Vc WS(5 Li) = WSnucl + Uc(Z=2) 0 p 3/2, 0 p 1/2 (resonant), contours of p 3/2 and p 1/2 scattering states SGI : Surface Gaussian Interaction: Coulomb interaction necessary Problem: long-range, lengthy 2 D complex scaling, divergences Solution: one-body long-range / two-body short-range separation H 0 one-body basis: October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 16

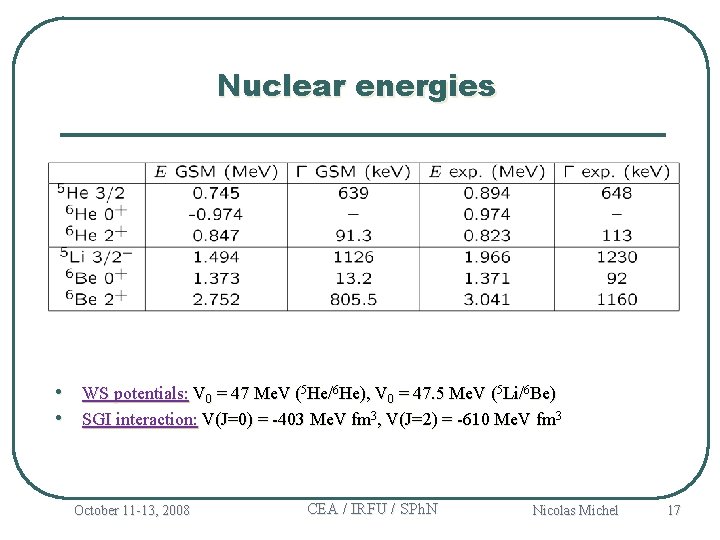
Nuclear energies • WS potentials: V 0 = 47 Me. V (5 He/6 He), V 0 = 47. 5 Me. V (5 Li/6 Be) • SGI interaction: V(J=0) = -403 Me. V fm 3, V(J=2) = -610 Me. V fm 3 October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 17

Spectroscopic factors in GSM • One particle emission channel: (l, j, p/n) • Basis-independent definition: • Experimental : all energies taken into account • Standard : representation dependence (n, l, j, p/n) • 5 He / 6 He, 5 Li / 6 Be : non resonant components necessary. October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 18

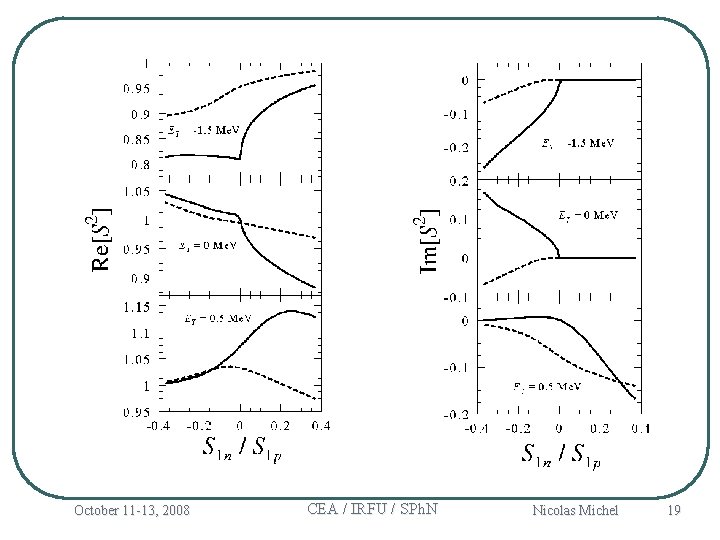
October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 19

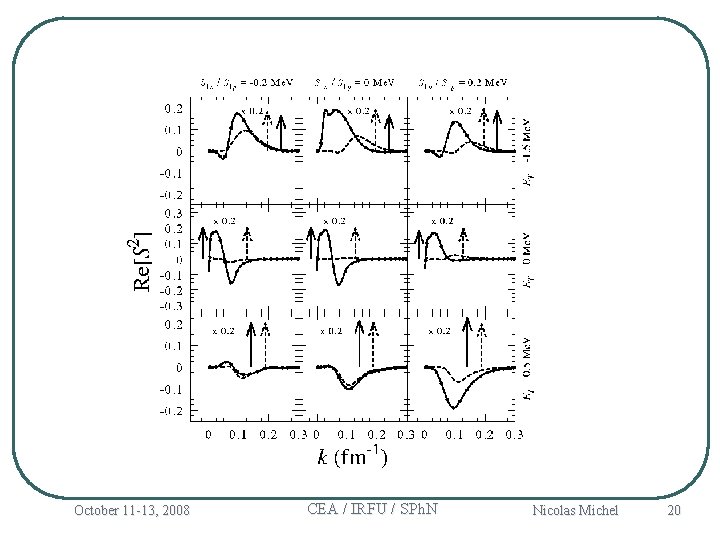
October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 20

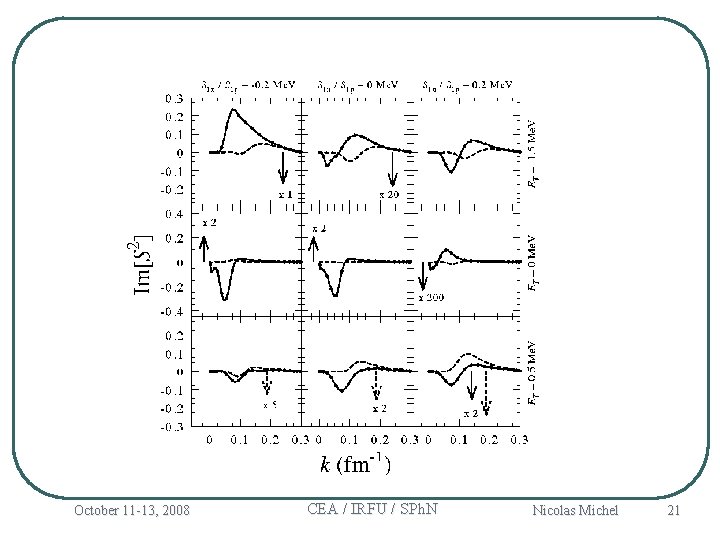
October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 21

Conclusion et perspectives Conclusion • SMEC and GSM: Two complementary models • SMEC: convenient for proton emitters, very small widths can be calculated Approximations needed for the moment, very complicated formulas Emission channels interfere: model-dependent description (cluster, sequential) • GSM: First calculations with several valence protons Simple and powerful model Spectroscopic factors: mirror effects due to continuum Perspectives • More realistic interactions to be used with SMEC and GSM • SMEC: full problem with three-body asymptotics possible • GSM: study of a larger set of light nuclei October 11 -13, 2008 CEA / IRFU / SPh. N Nicolas Michel 22