Shaping Modern Mathematics Raymond Flood Gresham Professor of

Shaping Modern Mathematics Raymond Flood Gresham Professor of Geometry

Lectures At the Museum of London • Ghosts of Departed Quantities: Calculus and its Limits Tuesday 25 September 2012 • Polynomials and their Roots Tuesday 6 November 2012 • From One to Many Geometries Tuesday 11 December 2012 • The Queen of Mathematics Tuesday 22 January 2013 • Are Averages Typical? Tuesday 19 February 2013 • Modelling the World Tuesday 19 March 2013

Ghosts of Departed Quantities: Calculus and its Limits Raymond Flood Gresham Professor of Geometry

What is the Calculus? Integration is used to find areas of shapes in twodimensional space or volumes in three dimensions.

Archimedes (c 287 – 212 BC) Archimedes, by Georg Andreas Böckler, 1661 the volume of a cylinder is 11/2 times that of the sphere it surrounds.

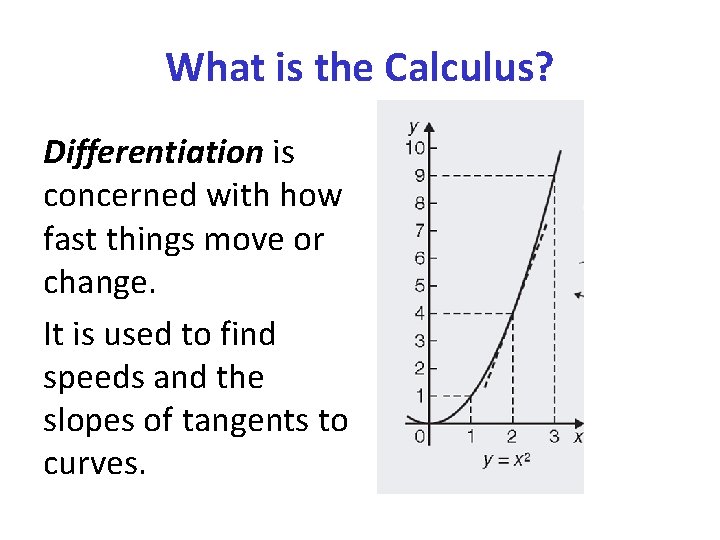
What is the Calculus? Differentiation is concerned with how fast things move or change. It is used to find speeds and the slopes of tangents to curves.

Apollonius’s Conics

David Gregory’s 1703 edition of Euclid’s Elements with Propositions from Euclid this time drawn on the sand Halley’s 1710 edition of Apollonius with conic sections drawn in the sand Torelli ‘s 1792 edition of Archimedes and this time with a spiral, in fact an Archimedean spiral, drawn in the sand.

Characterising the family of ideas called the calculus • A systematic way of finding tangents • A systematic way of finding areas • Connecting tangents and areas

Isaac Newton 1642 - 1727

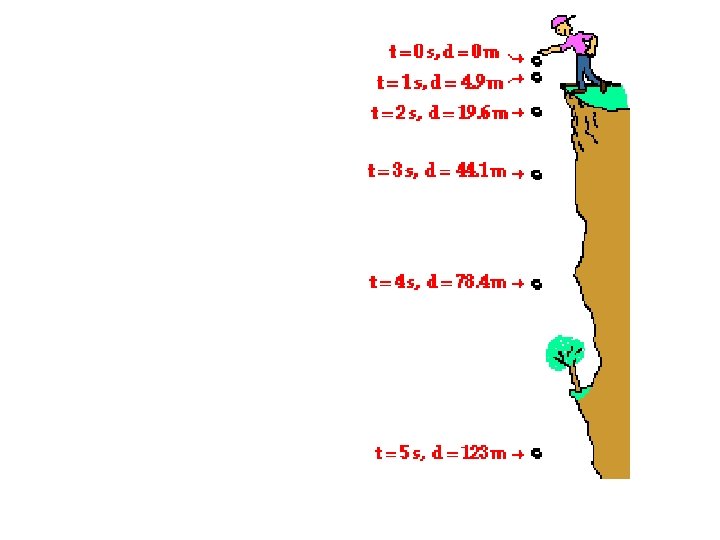
d = 4. 9 t 2

d = 4. 9 t 2 Average speed = distance travelled / time taken

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2 • In the time interval t to t + 0 distance travelled is 4. 9 (t + o)2 – 4. 9 t 2 = 9. 8 t o + 4. 9 o 2

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2 • In the time interval t to t + 0 distance travelled is 4. 9 (t + o)2 – 4. 9 t 2 = 9. 8 t o + 4. 9 o 2 • Divide by o to find average speed over the interval = 9. 8 t + 4. 9 o

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2 • In the time interval t to t + 0 distance travelled is 4. 9 (t + o)2 – 4. 9 t 2 = 9. 8 t o + 4. 9 o 2 • Divide by o to find average speed over the interval = 9. 8 t + 4. 9 o • Shrink the interval i. e. allow o to approach zero • Then this average speed, 9. 8 t + 4. 9 o, approaches the instantaneous speed 9. 8 t

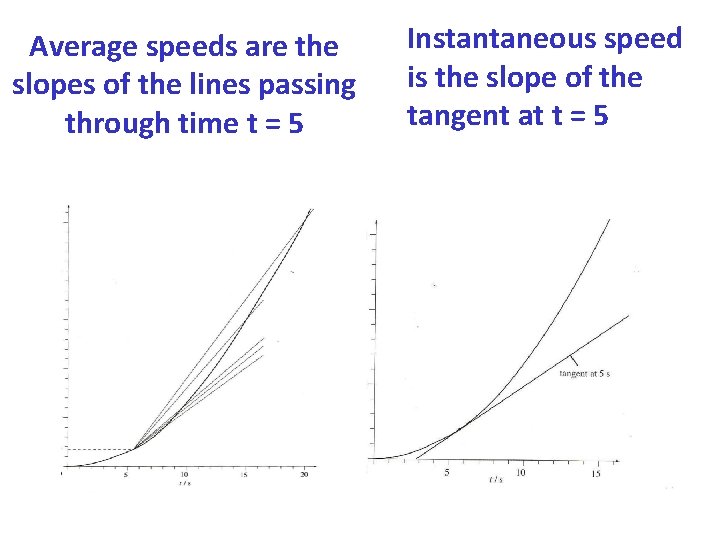
Average speeds are the slopes of the lines passing through time t = 5 Instantaneous speed is the slope of the tangent at t = 5

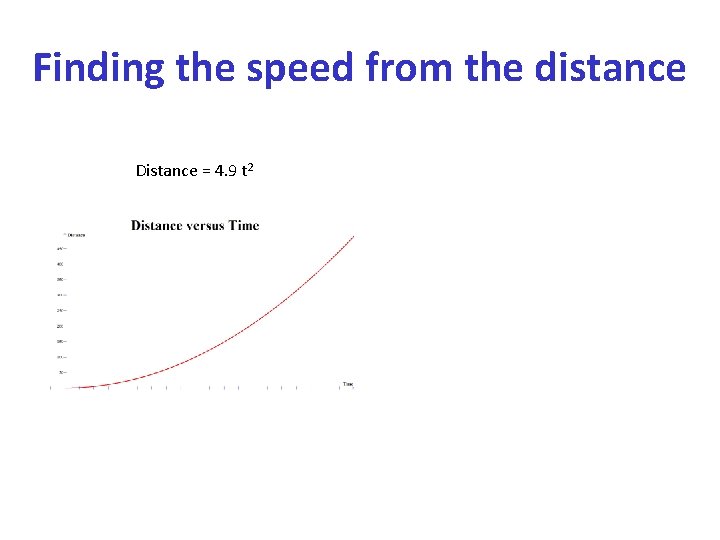
Finding the speed from the distance Distance = 4. 9 t 2

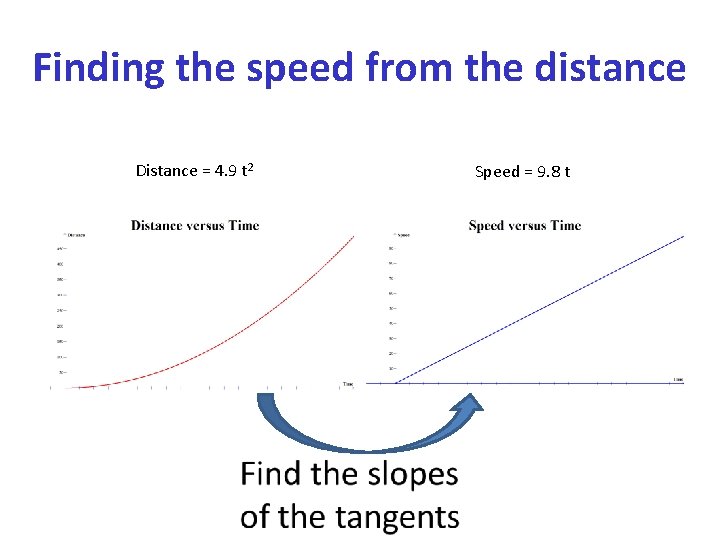
Finding the speed from the distance Distance = 4. 9 t 2 Speed = 9. 8 t

Finding the acceleration from the speed Speed = 9. 8 t

Finding the acceleration from the speed Speed = 9. 8 t Acceleration = 9. 8 Find the slopes of the tangents

DIFFERENTIATION Distance = 4. 9 t 2 Speed = 9. 8 t Find the slopes of the tangents Acceleration = 9. 8 Find the slopes of the tangents

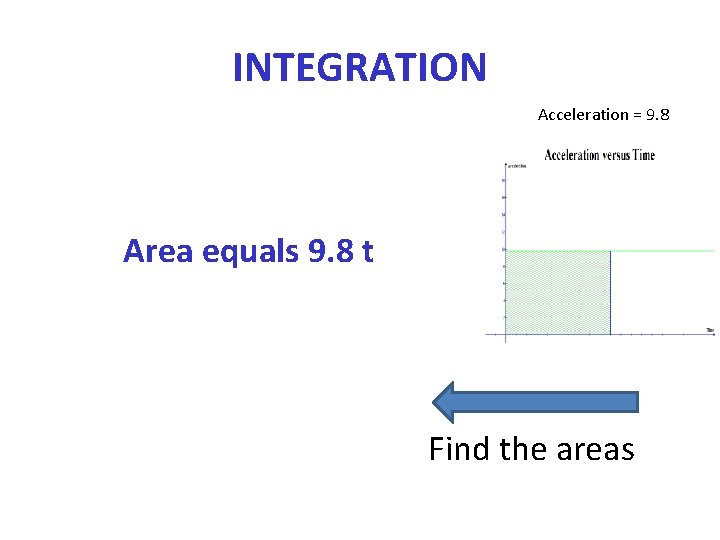
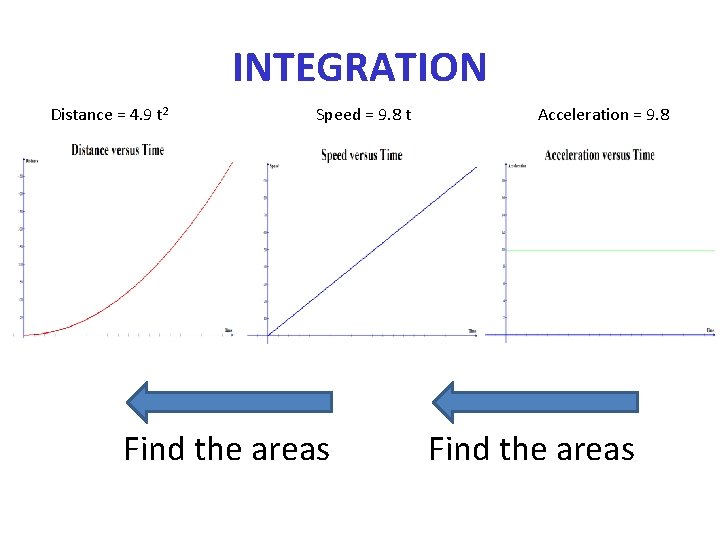
INTEGRATION Acceleration = 9. 8 Area equals 9. 8 t Find the areas

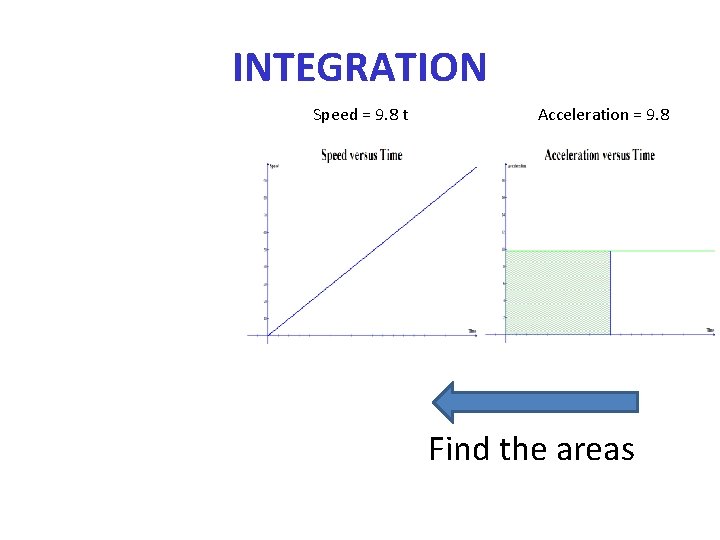
INTEGRATION Speed = 9. 8 t Acceleration = 9. 8 Find the areas

INTEGRATION Speed = 9. 8 t Acceleration = 9. 8 Area = 4. 9 t 2 Find the areas

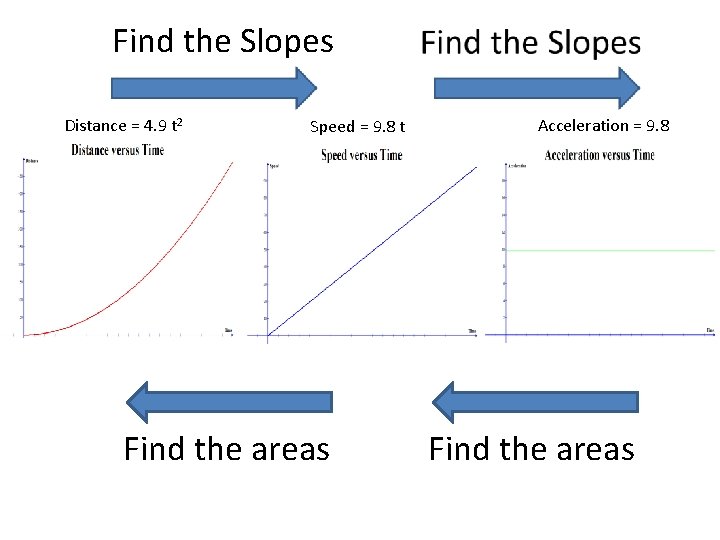
INTEGRATION Distance = 4. 9 t 2 Speed = 9. 8 t Find the areas Acceleration = 9. 8 Find the areas

Find the Slopes Distance = 4. 9 t 2 Speed = 9. 8 t Find the areas Acceleration = 9. 8 Find the areas

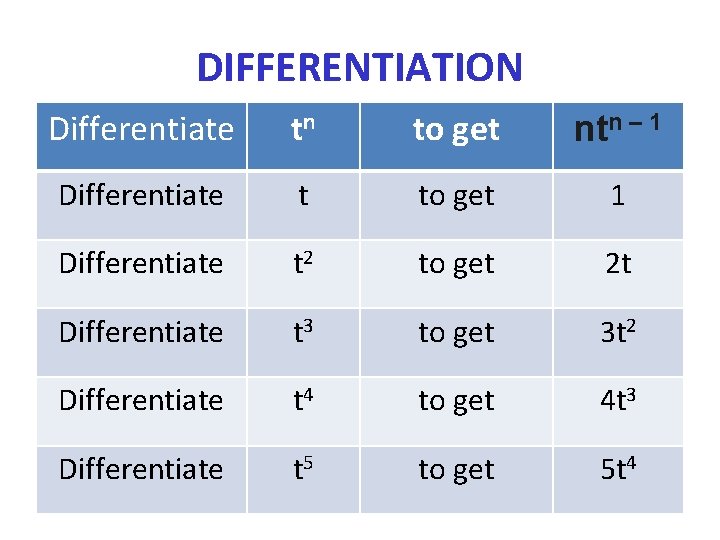
DIFFERENTIATION Differentiate t To get 1 Differentiate t 2 To get 2 t Differentiate t 3 To get 3 t 2 Differentiate t 4 To get 4 t 3 Differentiate t 5 To get 5 t 4

DIFFERENTIATION Differentiate tn to get ntn – 1 Differentiate t to get 1 Differentiate t 2 to get 2 t Differentiate t 3 to get 3 t 2 Differentiate t 4 to get 4 t 3 Differentiate t 5 to get 5 t 4

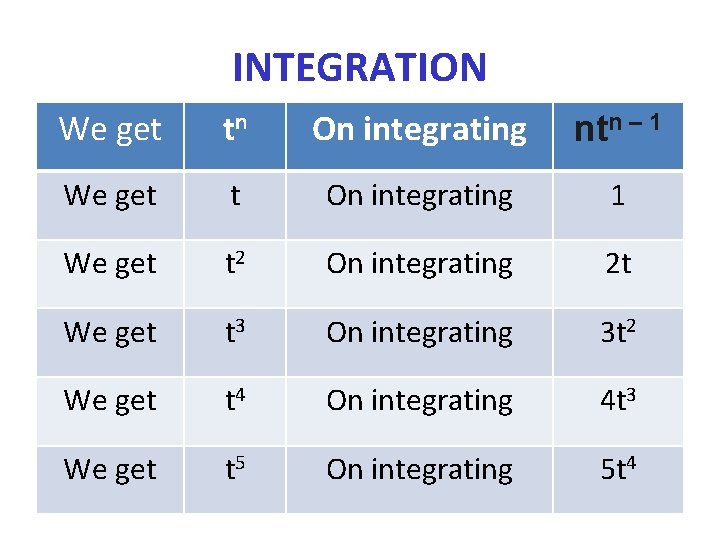
INTEGRATION We get tn On integrating ntn – 1 We get t On integrating 1 We get t 2 On integrating 2 t We get t 3 On integrating 3 t 2 We get t 4 On integrating 4 t 3 We get t 5 On integrating 5 t 4

Gottfried Leibniz 1646 - 1716

Binary Arithmetic It is possible to use … a binary system, so that as soon as we have reached two we start again from unity in this way: (0) (1) (2) (3) (4) (5) (6) (7) (8) 0 1 10 11 100 101 110 111 1000 … what a wonderful way all numbers are expressed by unity and nothing.

Leibniz’s Calculating machine The machine’s crucial innovation was a stepped gearing wheel with a variable number of teeth along its length, which allowed multiplication on turning a handle.

Leibniz notation d (or dy/dx) notation for differentiation: referring to the change in y divided by the change in x ∫ notation for the integration: finding areas under curves by summing lines. He defined omnia l (all the ls), which he then represented by an elongated S for sum, the integral sign, ∫.

First appearance of the Integral sign, ∫ on October 29 th 1675

Leibniz’s 1684 account of his Differential Calculus

Leibniz’s rules for differentiation • For any constant a: d(a) = 0, d(ay) = a dy • d(v + y) = dv + dy • d(vy) = v dy + y dv • d(v/y) = (y dv − v dy) / y 2

The Priority dispute Developed Calculus 1665 – 1667 Published 1704 -1736 Developed Calculus 1673– 1676 Published 1684 - 1686

Brachistochrone problem Suppose that you roll a ball down a ramp from a point A to another point B. Which curve should the ramp be if the ball is to reach B in the shortest possible time? Johann Bernoulli 1667 – 1748

A cycloid is the curve traced by a fixed point on a circle rolling along a straight line; one can think of a cycloid as the curve traced out by a piece of mud on a bicycle tyre when the bicycle is wheeled along.

Model to illustrate that the cycloid gives the path of quickest descent

Bishop Berkeley 1685 - 1753 If to be is to be perceived?

If to be is to be perceived? There was a young man who said God, Must find it exceedingly odd When he finds that the tree Continues to be When no one's about in the Quad. Dear Sir, your astonishment's odd I'm always about in the Quad And that's why the tree Continues to be Since observed by, yours faithfully, God Ronald Knox

Bishop Berkeley’s Queries • Query 64 Whether mathematicians, who are so delicate in religious points, are strictly scrupulous in their own science? Whether they do not submit to authority, take things upon trust, and believe points inconceivable’? Whether they have not their mysteries, and what is more, their repugnancies and contradictions?

And what are these same evanescent Increments? They are neither finite Quantities nor Quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2 • In the time interval t to t + 0 distance travelled is 4. 9 (t + o)2 – 4. 9 t 2 = 9. 8 t o + 4. 9 o 2 • Divide by o to find average speed over the interval = 9. 8 t + 4. 9 o • Shrink the interval i. e. allow o to approach zero • Then this average speed, 9. 8 t + 4. 9 o, approaches the instantaneous speed 9. 8 t

Dividing by Zero To Prove that 5 = 8 0 x 5 = 0 x 8 as they are both 0. If we are able to divide by 0 and do so we get 5 = 8

Finding instantaneous speed from average speed • Distance travelled in time t equals 4. 9 t 2 • At a later time, t + o, distance travelled is: 4. 9 (t + o)2 • In the time interval t to t + 0 distance travelled is 4. 9 (t + o)2 – 4. 9 t 2 = 9. 8 t o + 4. 9 o 2 • Divide by o to find average speed over the interval = 9. 8 t + 4. 9 o • Shrink the interval i. e. allow o to approach zero • Then this average speed, 9. 8 t + 4. 9 o, approaches the instantaneous speed 9. 8 t

Limit Bernard Bolzano 1781 – 1849 Jean-Baptiste le Rond d'Alembert, 1717 – 1783 Augustin-Louis Cauchy (1789 – 1857)

Earthrise Apollo 8, December 24 th 1968

Polynomials and their Roots Tuesday 6 th November 2012 X 2 - 8 X + 15 = 0 has two real solutions. X 2 - 8 X + 16 = 0 has one real solution. X 2 - 8 X + 17 = 0 has no real solutions.

19 th Century Mathematical Physics Wednesday, 31 October 2012 - 4: 00 pm Barnard’s Inn Hall A series of talks on Lord Kelvin, Peter Guthrie Tait and James Clerk Maxwell By Mark Mc. Cartney, Julia Collins and Raymond Flood