Shape Compression using Spherical Geometry Images Hugues Hoppe

Shape Compression using Spherical Geometry Images Hugues Hoppe, Microsoft Research Emil Praun, University of Utah

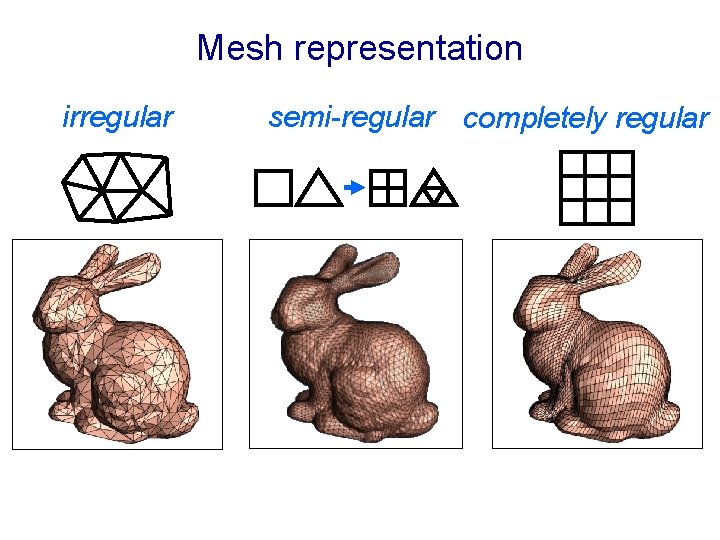
Mesh representation irregular semi-regular completely regular

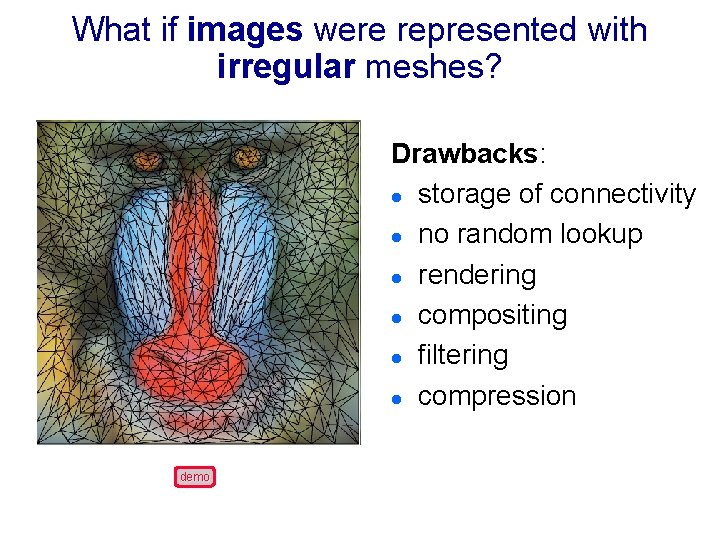
What if images were represented with irregular meshes? Drawbacks: l storage of connectivity l no random lookup l rendering l compositing l filtering l compression demo

Simple 2 D grid Advantages: l implicit connectivity l 2 D lookup l raster-scan l alpha blending l DSP l JPEG 2000

Representations for media l Audio: uniform 1 D grid l Images: uniform 2 D grid l Video: uniform 3 D grid l Geometry: irregular mesh historical artifact?

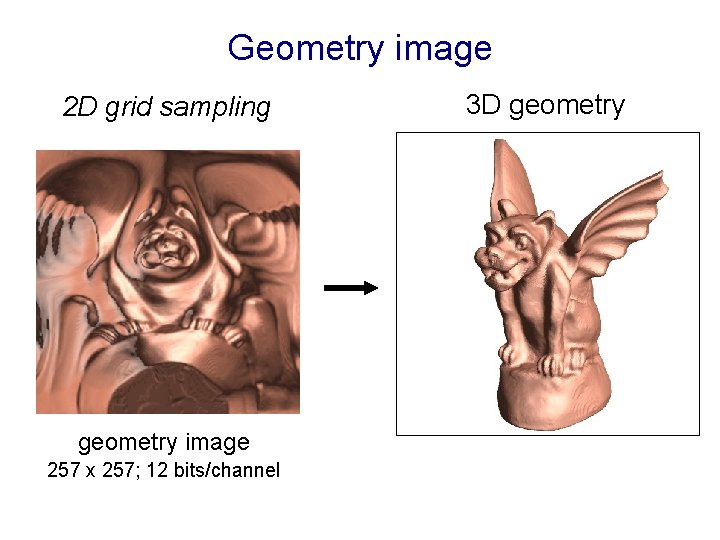
Geometry image 2 D grid sampling geometry image 257 x 257; 12 bits/channel 3 D geometry

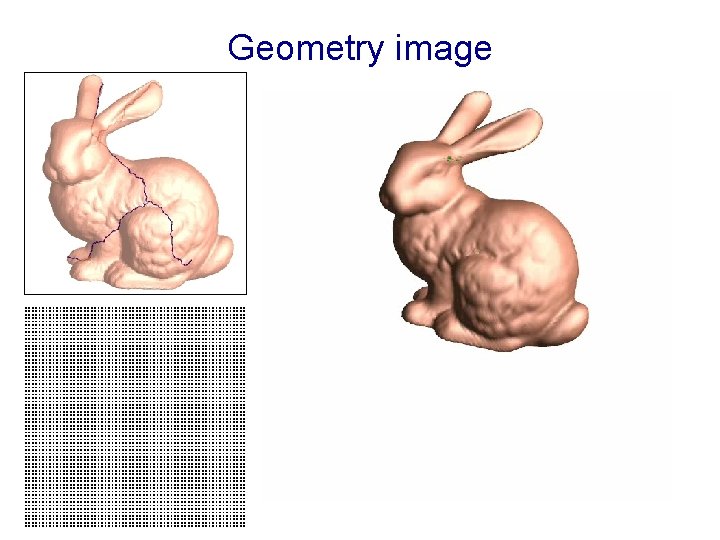
Geometry image

Geometry image render [r, g, b] = [x, y, z]

Advantages for hardware rendering l Regular sampling no vertex indices. l Sequential traversal of source data l Unified parametrization no texture coordinates.

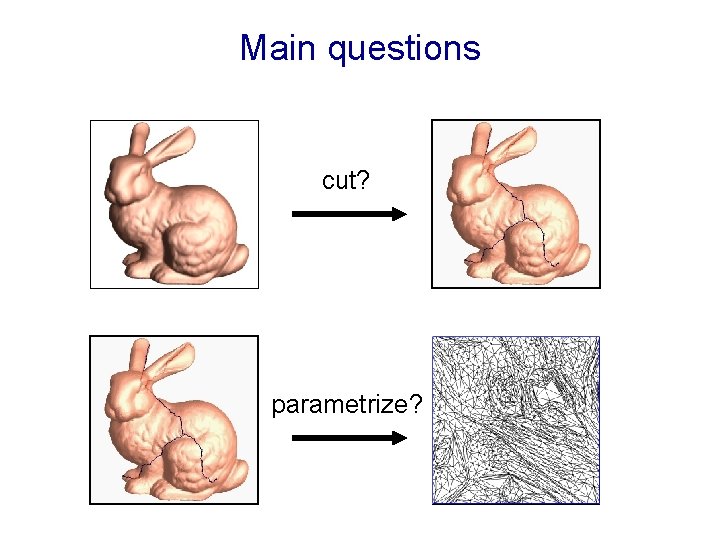
Main questions cut? parametrize?

Construction approaches General cut Spherical Multi-chart [Gu et al. SIGGRAPH 2002] [Praun & Hoppe. SIGGRAPH 2003] [Sander et al. SGP 2003] arbitrary surface genus-zero surface >1 chart cut symmetries zippering

Construction approaches General cut [Gu et al. SIGGRAPH 2002] arbitrary surface genus 6

Construction approaches General cut Spherical Multi-chart [Gu et al. SIGGRAPH 2002] [Praun & Hoppe. SIGGRAPH 2003] [Sander et al. SGP 2003] arbitrary surface genus-zero surface >1 chart cut symmetries zippering 400 x 160 piecewise regular

Construction approaches General cut Spherical Multi-chart [Gu et al. SIGGRAPH 2002] [Praun & Hoppe. SIGGRAPH 2003] [Sander et al. SGP 2003] arbitrary surface genus-zero surface >1 chart cut symmetries zippering

Spherical parameterization and remeshing [Praun, Hoppe 2003]

Spherical parameterization and remeshing [Praun, Hoppe 2003]

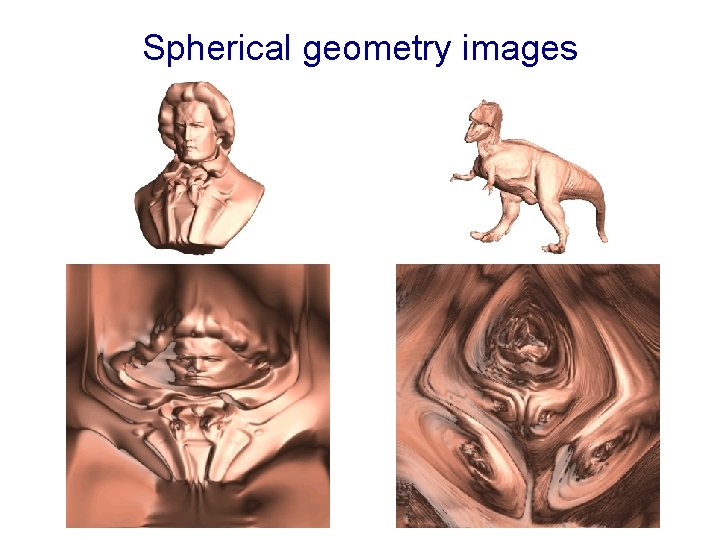
Spherical geometry images

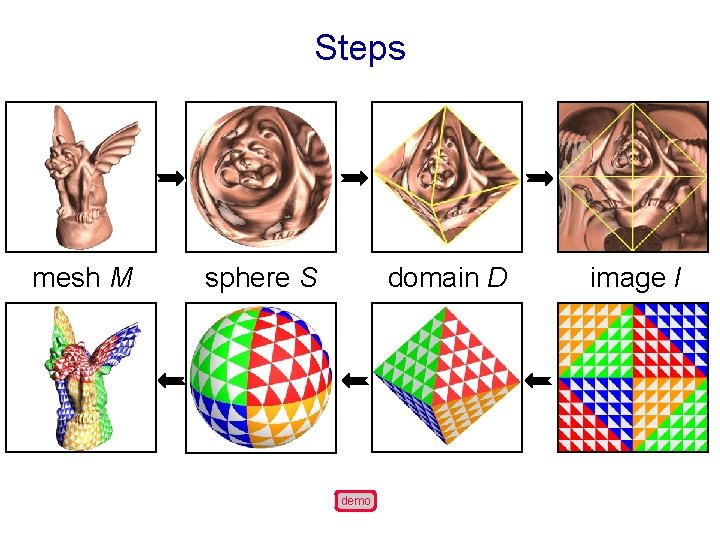
Steps mesh M sphere S domain D demo image I

Spherical parametrization [Kent et al. 1992] [Haker et al. 2000] [Alexa 2002] [Grimm 2002] [Sheffer et al. 2003] [Gotsman et al. 2003] mesh M l sphere S Two challenges: n robustness n good sampling stretch metric coarse-to-fine [Hormann et al. 1999] [Sander et al. 2001] [Sander et al. 2002]

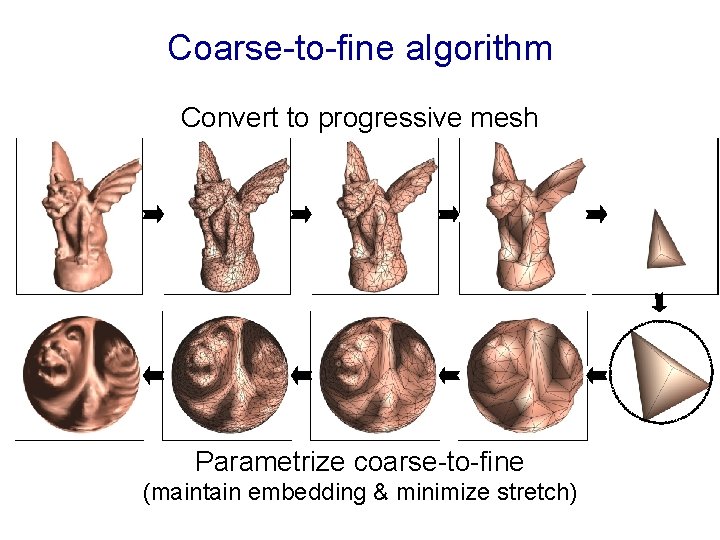
Coarse-to-fine algorithm Convert to progressive mesh Parametrize coarse-to-fine (maintain embedding & minimize stretch)

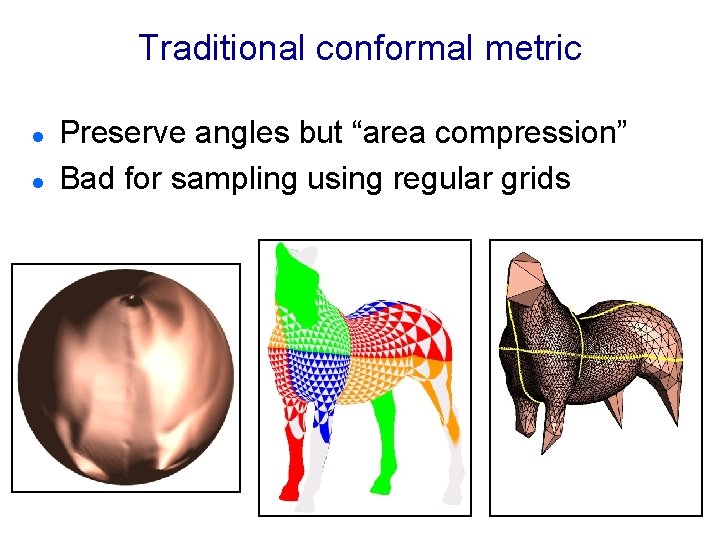
Traditional conformal metric l l Preserve angles but “area compression” Bad for sampling using regular grids

Stretch metric l l Penalizes undersampling Better samples the surface [Sander et al. 2001] [Sander et al. 2002]

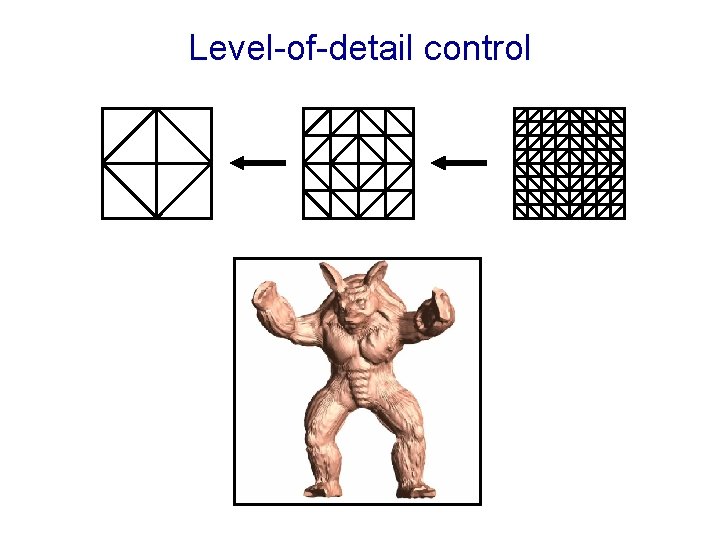
Applications of spherical remeshing l Level-of-detail control l Morphing l Geometry amplification l Shape compression

Level-of-detail control

Morphing l l Align meshes on the sphere. Interpolate the resulting geometry images.

Geometry amplification simulation [Losasso et al. SGP 2003] “smooth geometry images” CPU GPU 33 x 33 65 x 65 floating-point geometry image 129 x 129 257 x 257 + 257 x 257 scalar displacements demo

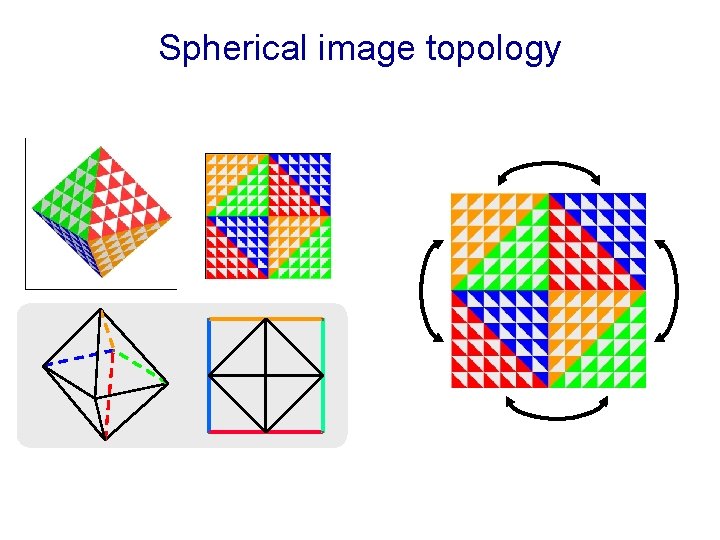
Shape compression (Genus-zero shapes) l Spherical image topology l Infinite 2 D tiling l Wavelets on regular 2 D grid

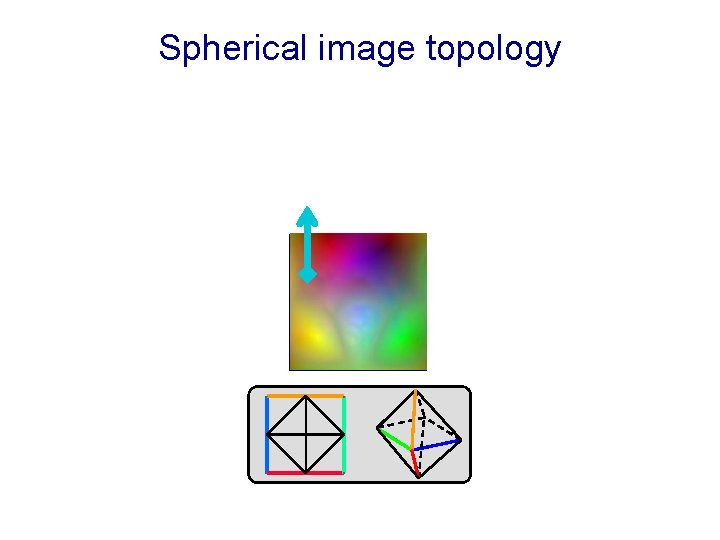
Spherical image topology

Spherical image topology

Spherical image topology

Infinite 2 D tiling

Wavelets on regular 2 D grid spherical wavelets image wavelets [Schröder & Sweldens 1995] [Davis 1995] [Antonini et al 1992]

Test models

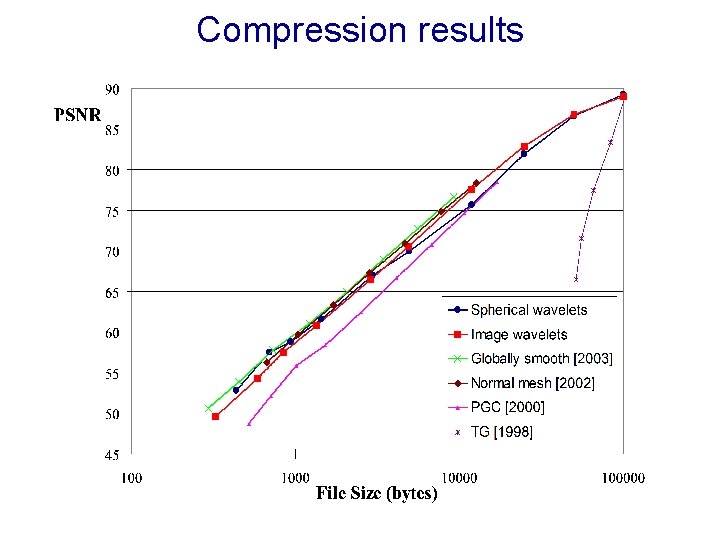
Compression results

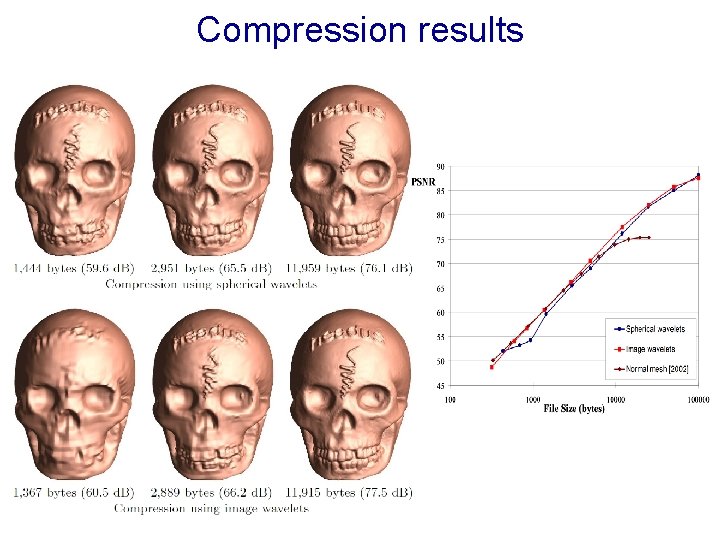
Compression results

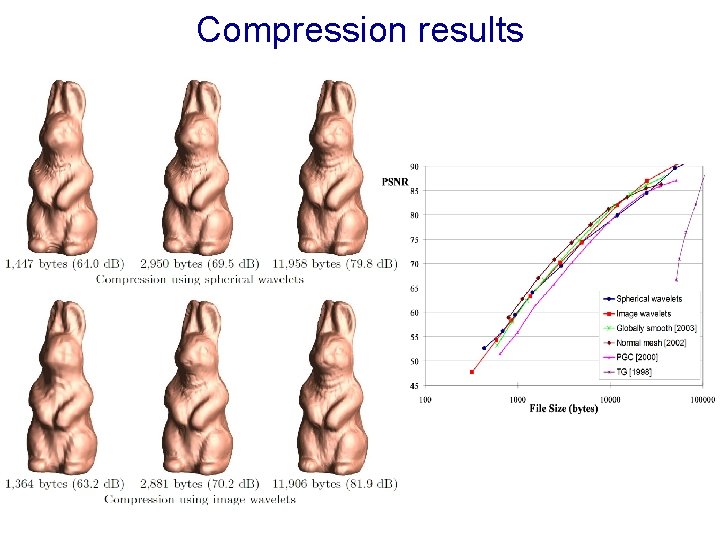
Compression results

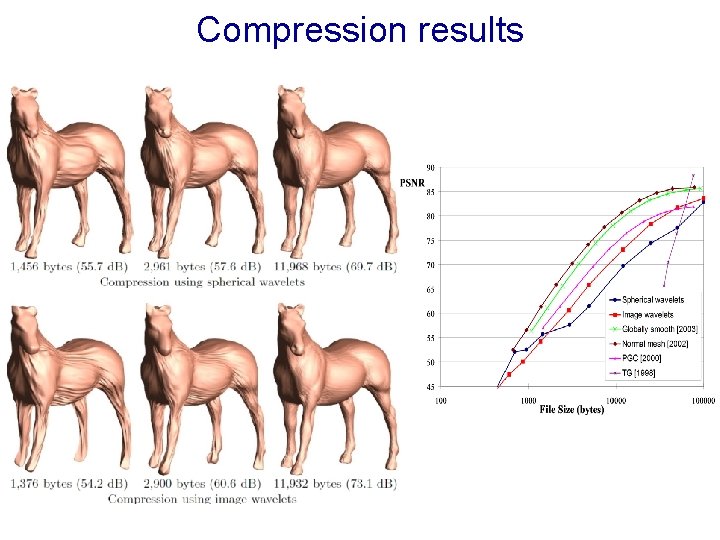
Compression results

Compression results

Summary l Geometry image n l Simplicity of 2 D grid Applications n n n Rendering LOD Morphing Geometry amplification Shape compression

Future work l Visual error metrics [Touma & Gotsman 1998] [Sorkine et al 2003] l Attenuation of rippling artifacts l Surface boundaries l Animated meshes “geometry videos” [Briceño et al 2003]