Sezione durto t ondulatoria Molti tipi di collisioni

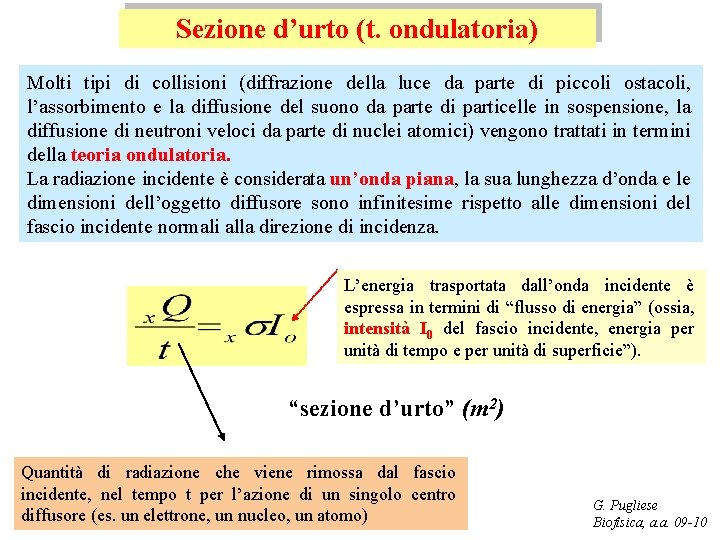
Sezione d’urto (t. ondulatoria) Molti tipi di collisioni (diffrazione della luce da parte di piccoli ostacoli, l’assorbimento e la diffusione del suono da parte di particelle in sospensione, la diffusione di neutroni veloci da parte di nuclei atomici) vengono trattati in termini della teoria ondulatoria. La radiazione incidente è considerata un’onda piana, la sua lunghezza d’onda e le dimensioni dell’oggetto diffusore sono infinitesime rispetto alle dimensioni del fascio incidente normali alla direzione di incidenza. L’energia trasportata dall’onda incidente è espressa in termini di “flusso di energia” (ossia, intensità I 0 del fascio incidente, energia per unità di tempo e per unità di superficie”). “sezione d’urto” (m 2) Quantità di radiazione che viene rimossa dal fascio incidente, nel tempo t per l’azione di un singolo centro diffusore (es. un elettrone, un nucleo, un atomo) G. Pugliese Biofisica, a. a. 09 -10

Esempio: scattering Thomson Un elettrone libero che viene investito da un’onda elettromagnetica piana polarizzata (fotone) accelera sotto l’effetto del campo elettrico e, di conseguenza, emette radiazione verso direzioni anche diverse dalla direzione dell’onda incidente. Se la frequenza ν dell’onda è tale che hν<< mec 2, il processo di diffusione può essere esaminato da un punto di vista classico La potenza irradiata istante per istante e quella media sono (F. Larmor) G. Pugliese Biofisica, a. a. 09 -10

Esempio: scattering Thomson Questa energia è assorbita dal fascio incidente e riemessa in altra direzione; essa può essere espressa in termini della sezione d’urto σT, per elettrone: Poiché l’intensità del fascio incidente La sezione d’urto totale es, è definita come rapporto tra la potenza diffusa e il flusso incidente, indipendentemente da come viene diffusa la potenza scatterata. (cm 2/elettrone) Ha le dimensioni di una lunghezza, nota come “raggio classico dell’elettrone”. Compare in moltissimi tipi di interazioni, (non và tuttavia interpretata in termini di dimensioni dell’elettrone) G. Pugliese Biofisica, a. a. 09 -10

Sezione d’urto differenziale Ø Se più processi differenti contribuiscono a diminuire l’intensità del fascio incidente (processi in competizione l’uno con l’altro, per esempio ionizzazione e Bremsstrahlung per gli elettroni) allora di parla di sezioni d’urto parziali per ogni tipo di interazione. ØLa nozione di “sezione d’urto differenziale” viene spesso introdotta per rappresentare, in ogni interazione, il particolare meccanismo che contribuisce alla perdita della potenza del fascio osservato. Il particolare meccanismo dello scatt. Thomson che diffonde la potenza nell’angolo solido d individuato dalla direzione ξ ha una “sezione d’urto differenziale”: G. Pugliese Biofisica, a. a. 09 -10

Esempio: scattering Thomson Ø le sezioni d’urto Thomson sono indipendenti dalla frequenza. Ø valida solamente nel limite e solo se l’elettrone è libero. hν> > mec 2 Gli effetti relativistici provocano un sensibile abbassamento della sezione d’urto differenziale. La sezione totale diventa sempre più piccola via che aumenta l’energia del fotone incidente. Poiché mec 2 =511 Ke. V , la deviazione dalla formula classica avviene già nella banda ultravioletta estrema, ma diventa G. Pugliese importante solo nella regione X. Biofisica, a. a. 09 -10

Sezione d’urto (t. ondulatoria) La sezione d’urto compare come proprietà dell’interazione, descritta come un’area sx (cm 2) sul fronte d’onda incidente. L’energia x. Q rimossa dal fascio incidente è equivalente all’energia contenuta nel cilindro di sezione sx e altezza t Si consideri un foglio assorbente di superficie S (cm 2) e spessore dx (cm), supponiamo che la particella bersaglio sia uno degli elettroni atomici. Il numero di bersagli è: Dove N è il numero di atomi/cm 3 contenuti nel foglio assorbitore e Z il numero di elettroni di ogni atomo. IPOTESI: il foglio sia normale alla direzione di propagazione dell’onda piana indefinita e che ogni elettrone interagisca con l’onda in modo indipendente dagli altri elettroni (scattering incoerente). G. Pugliese Biofisica, a. a. 09 -10

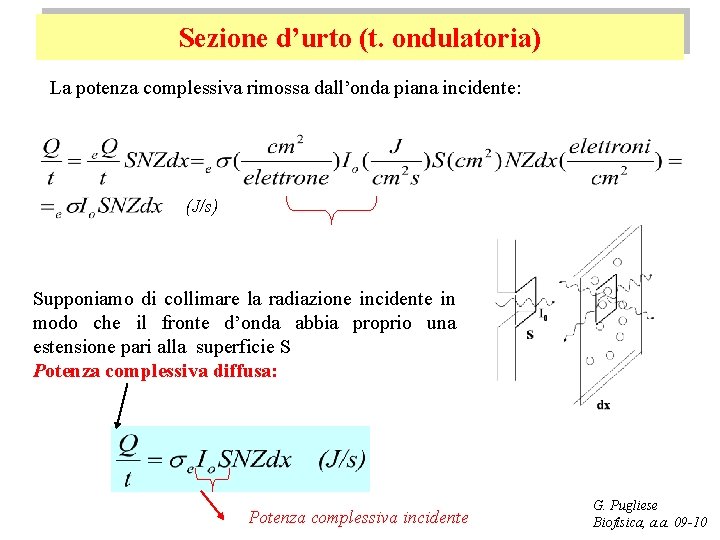
Sezione d’urto (t. ondulatoria) La potenza complessiva rimossa dall’onda piana incidente: (J/s) Supponiamo di collimare la radiazione incidente in modo che il fronte d’onda abbia proprio una estensione pari alla superficie S Potenza complessiva diffusa: Potenza complessiva incidente G. Pugliese Biofisica, a. a. 09 -10

Sezione d’urto (t. corpuscolare) Supponiamo che l’onda piana, dell’esperimento precedente, sia quantizzata. Per es. un’onda elettromagnetica la radiazione appare divisa in fotoni di energia hν. Il numero di fotoni sono n trasportati nel tempo t: Potenza diffusa Il numero di fotoni rimossi dal fascio collimato in ogni secondo La frazione di particelle incidenti rimossa dal fascio (indipendente dal tempo t e dalla superficie S dell’assorbitore ) G. Pugliese Biofisica, a. a. 09 -10

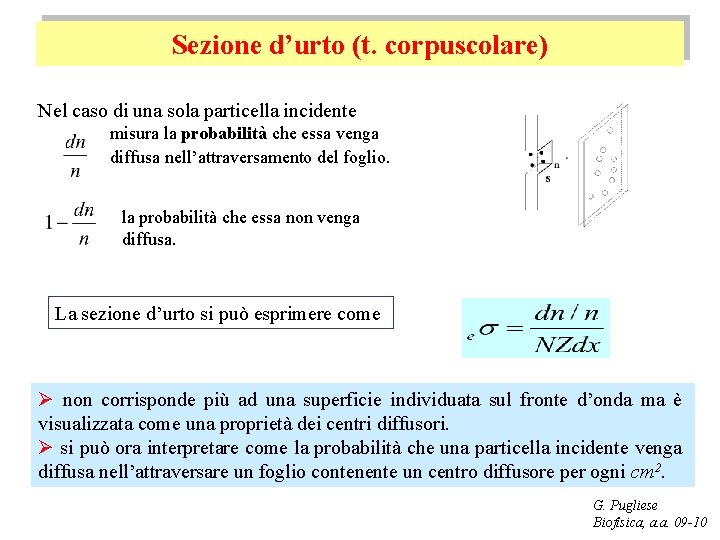
Sezione d’urto (t. corpuscolare) Nel caso di una sola particella incidente misura la probabilità che essa venga diffusa nell’attraversamento del foglio. la probabilità che essa non venga diffusa. La sezione d’urto si può esprimere come Ø non corrisponde più ad una superficie individuata sul fronte d’onda ma è visualizzata come una proprietà dei centri diffusori. Ø si può ora interpretare come la probabilità che una particella incidente venga diffusa nell’attraversare un foglio contenente un centro diffusore per ogni cm 2. G. Pugliese Biofisica, a. a. 09 -10

Coefficiente lineare di assorbimento La potenza diffusa da un foglio sottile di assorbitore di superficie S e spessore dx L’intensità perduta nell’attraversamento dello spessore compreso tra x e x+d, se I è l’intensità del fascio incidente alla profondità x: L’intensità della radiazione che viene trasmessa, senza essere diffusa, fino alla profondità x è allora: Posto: Coefficiente lineare di assorbimento G. Pugliese Biofisica, a. a. 09 -10

Coefficiente lineare di assorbimento La lunghezza L = 1/m rappresenta la distanza media che un singolo componente del fascio incidente (un fotone, un elettrone, etc. ) percorre nell’assorbitore prima di essere diffuso (a seconda dei casi: lunghezza di radiazione, lunghezza di conversione, lunghezza di collisione etc. ) G. Pugliese Biofisica, a. a. 09 -10

I coefficienti di interazione usati in dosimetria • Coefficiente di attenuazione massico (m 2 kg-1): pari al coefficiente lineare di attenuazione diviso la densità del mezzo. Esso ha la proprietà di essere indipendente dallo stato fisico e della densità del mezzo. • Coefficiente di trasferimento di energia massico: Dove d. Etr/EN rappresenta la frazione di energia dei fotoni incidenti trasferita in energia cinetica di particelle cariche secondarie a causa dell’interazione nel tratto dl del mezzo di densità r. G. Pugliese Biofisica, a. a. 09 -10

I coefficienti di interazione usati in dosimetria • Coefficiente di assorbimento di energia massico (consente di determinare l’energia effettivamente depositata in un certo volume) Dove g è la frazione di energia che i secondari carichi dissipano in radiazione di frenamento nel materiale. G. Pugliese Biofisica, a. a. 09 -10

A titolo indicativo viene riportato in tabella il percorso medio in aria e nei tessuti delle radiazioni a, b e g di 1 Me. V. Tipo di radiazione Percorso in aria Percorso nel tessuto a 0. 7 cm 0. 006 cm b 2. 3 m 0. 43 cm g circa 300 m 31. 3 cm G. Pugliese Biofisica, a. a. 09 -10