Severity Distributions for GLMs Gamma or Lognormal Presented

Severity Distributions for GLMs: Gamma or Lognormal? Presented by Luyang Fu, Grange Mutual Richard Moncher, Bristol West 2004 CAS Spring Meeting Colorado Springs, Colorado May 18, 2004 1

Session Outline Introduction Distribution Assumptions Simulation Method Simulation Results Conclusions 2

Introduction Common characteristics of loss distributions Typical GLM forms in actuarial practice Lognormal and Gamma are most widely-used distributions in size of loss (severity) analysis Lognormal or Gamma? 3

Distribution Characteristics of Insurance Losses Non-negative Positively skewed Variance is positively correlated with mean. Normal is not appropriate: negative, symmetric, constant variance 4

Advantages of GLMs Exponential Distribution Selections: Poisson, Gamma, Binomial, Inverse Gaussian, Negative Binomial, etc. Lognormal is not in exponential family. Link Function Selections: Identity, Logit, Power, Probit, etc. 5

Typical GLM Forms in Actuarial Practice Severity: Log link, Gamma Distribution Frequency: Log link, Poisson Distribution Retention (Renewal): Logit link, Binomial Distribution 6

Gamma or Lognormal? Gamma and lognormal are the two most popular selections of loss distributions On CAS website (www. casact. org), we found 31 papers by searching “Lognormal” and 37 papers by searching “Gamma” 7

Lognormal Is One of Most Widely-Used Loss Distributions Proceedings of the Casualty Actuarial Society Ratemaking and Reinsurance Wacek, Michael G. (1997) Bear, Robert A. ; Nemlick, Kenneth J. (1990) Hayne, Roger M. (1985) Mack, Thomas (1984) Ter Berg, Peter (1980) Benckert, Lars-Gunnar (1962) 8

Lognormal Is One of Most Widely-Used Loss Distributions Proceedings of the Casualty Actuarial Society Reserving and Reinsurance Kreps, Rodney E. (1997) Ramsay, Colin M. ; Usabel, Miguel A. (1997) Doray, Louis G. (1996) Levi, Charles; Partratm, Christian (1991) Hertig, Joakim (1985) 9

Lognormal Is One of Most Widely-Used Loss Distributions In actuarial practice Increased Limit Factors Excess of Loss Calculations Weather Load Quantile Loss Reserve Variability 10

Gamma or Lognormal? Desirable Features of Gamma and Lognormal Distributions: 1. Non-negative 2. Positively skewed 3. Variance is proportional to the meansquared (Constant Coefficient of Variation) 11

Gamma or Lognormal? Advantages of Lognormal: Easy to understand (related to normal distribution) Consistent with other actuarial procedures, such as increased limits ratemaking Fits data with large skewness well Disadvantage of Lognormal: Not in exponential family, and GLM coefficients need volatility adjustment 12

Gamma or Lognormal? Under what conditions are the severity distribution assumptions important? If severity distribution is unknown, which distribution yields most accurate and stable results (i. e. , minimized estimation bias and standard error)? 13

Classical Distribution Assumptions Normal Constant Variance Gamma Constant Coefficient of Variation 14

Classical Distribution Assumptions Lognormal Constant Coefficient of Variation 15

Does Normal Necessarily Imply Constant Variance? Normal Constant Coefficient of Variation: Variance function is like Gamma Normal Variance proportional to mean: Variance function is like Poisson 16

Does Gamma Necessarily Imply Constant Coefficient of Variation? Gamma Variance is proportional to mean: Variance function is like Poisson. 17

Distribution Assumptions One of two parameters is constant Which one is selected as constant should be based on data Classical assumptions are most-widely used distribution forms, and generally fit data better Can we assume none of them are constant? Yes, but it will increase the number of parameters and reduce the degrees of freedom 18

Why Simulation? The distributions of GLM coefficients and predicted values are unknown in the case of small samples Statistical analysis based on asymptotic distributions is not reliable In an individual regression, we don’t know if the difference between predicted value and observed value is from random variation or systematic bias 19

Simulation Assumptions 32 Severity Observations for Two Class Variables 8 Age Groups 4 Vehicle-Use Groups Data Source: Private Passenger Auto Collision used in Mildenhall (1999) and Mc. Cullagh and Nelder (1989) 20

Simulation Assumptions Individual Losses Have Constant Coefficient of Variation Multiplicative Relationship Between Severities and Rating Variables Known “True” Base Severities & Relativities Known CVs for the Severity Distribution 21

Simulation Procedures 1. 2. 3. Generate individual losses based on lognormal and gamma distributions and calculate 32 claim severities Fit three regressions: GLM with Gamma, GLM with Normal, and GLM with logtransformed severity Repeat Steps 1 -2 one thousand times, and generate sampling distributions of GLM coefficients and predicted values 22

Performance Measurements Weighted Absolute Bias, which measures the systematic bias (accuracy): Weighted Standard Error, which measures random variation (stability): 23

Adjustments for Log-Transformed Regressions GLMs with Gamma and Normal Log-transformed Regression is called the “Volatility Adjustment Factor” 24

Simulation Results Data Generated Regression Results Residual Diagnostics 25

Data Generated Reporting on Two Different Classes: Classification I - Age 17 -20 and Pleasure Use, with 21 observations. Classification II - Age 40 -49 and Short Drive to Work, with 970 observations. 26

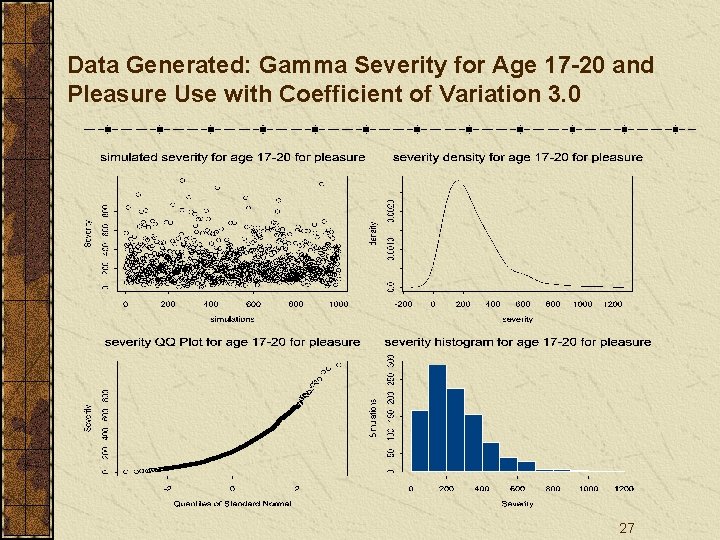
Data Generated: Gamma Severity for Age 17 -20 and Pleasure Use with Coefficient of Variation 3. 0 27

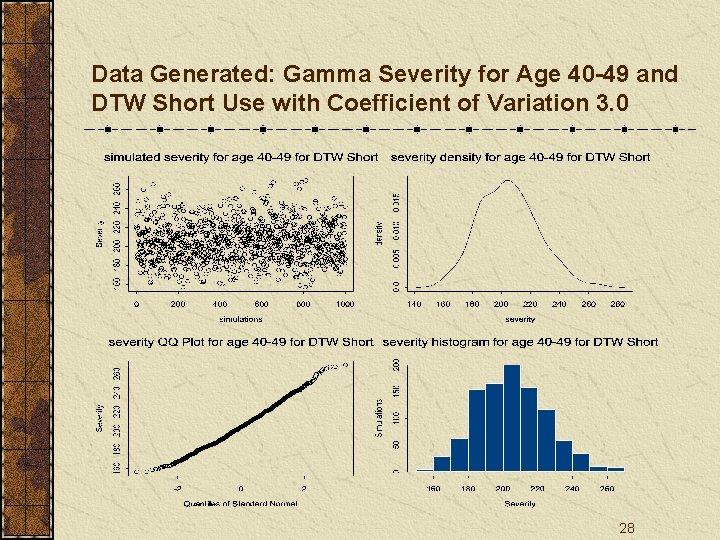
Data Generated: Gamma Severity for Age 40 -49 and DTW Short Use with Coefficient of Variation 3. 0 28

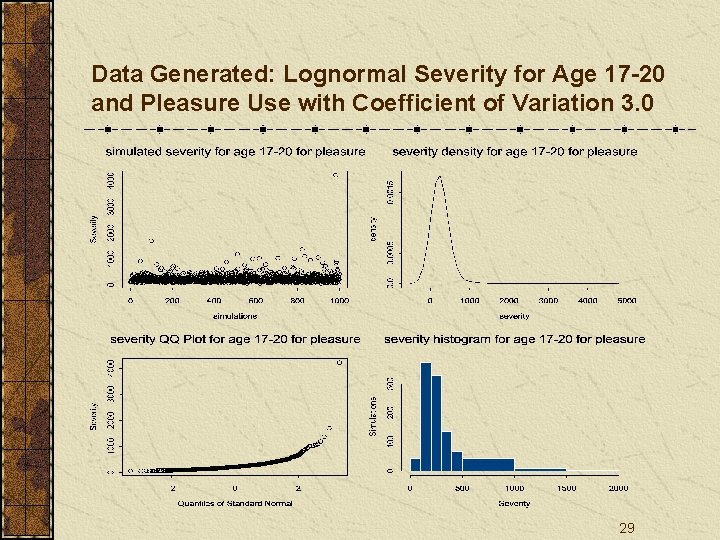
Data Generated: Lognormal Severity for Age 17 -20 and Pleasure Use with Coefficient of Variation 3. 0 29

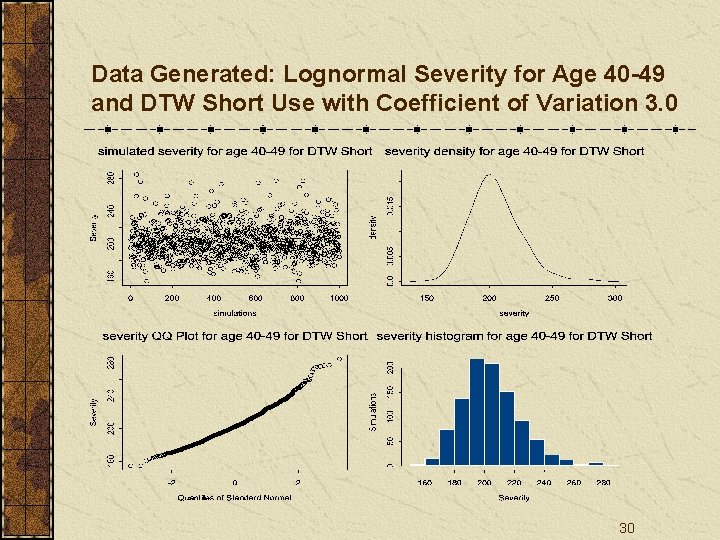
Data Generated: Lognormal Severity for Age 40 -49 and DTW Short Use with Coefficient of Variation 3. 0 30

Regression Results Overall Unbiasedness and Stability of Predicted Severities for Gamma Loss CV wse wab G-G G-L G-N 1. 0 0. 180 0. 240 0. 221 8. 170 8. 177 8. 568 2. 0 0. 475 0. 852 0. 509 16. 498 16. 514 17. 239 3. 0 0. 860 1. 808 1. 139 25. 223 25. 097 26. 986 31

Regression Results Overall Unbiasedness and Stability of Predicted Severities for Lognormal Loss CV wse wab L-G L-L L-N 1. 0 0. 151 0. 202 0. 175 8. 309 8. 284 8. 754 2. 0 0. 498 0. 844 0. 604 16. 426 16. 113 17. 721 3. 0 0. 720 1. 589 1. 006 24. 328 23. 214 27. 608 32

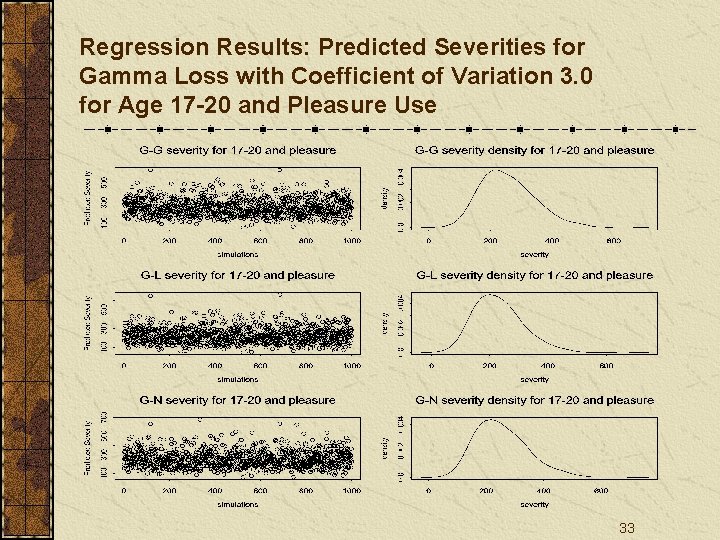
Regression Results: Predicted Severities for Gamma Loss with Coefficient of Variation 3. 0 for Age 17 -20 and Pleasure Use 33

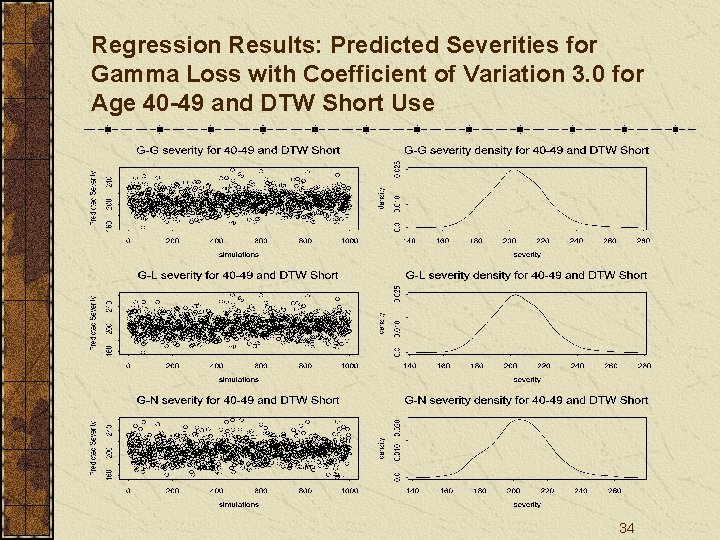
Regression Results: Predicted Severities for Gamma Loss with Coefficient of Variation 3. 0 for Age 40 -49 and DTW Short Use 34

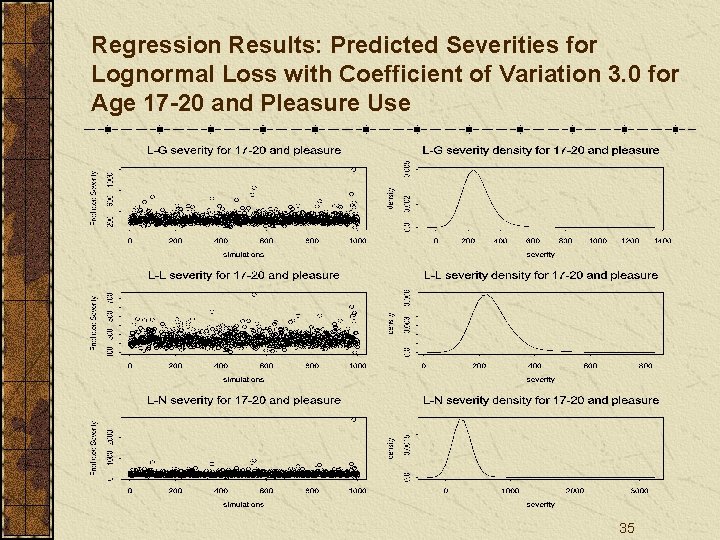
Regression Results: Predicted Severities for Lognormal Loss with Coefficient of Variation 3. 0 for Age 17 -20 and Pleasure Use 35

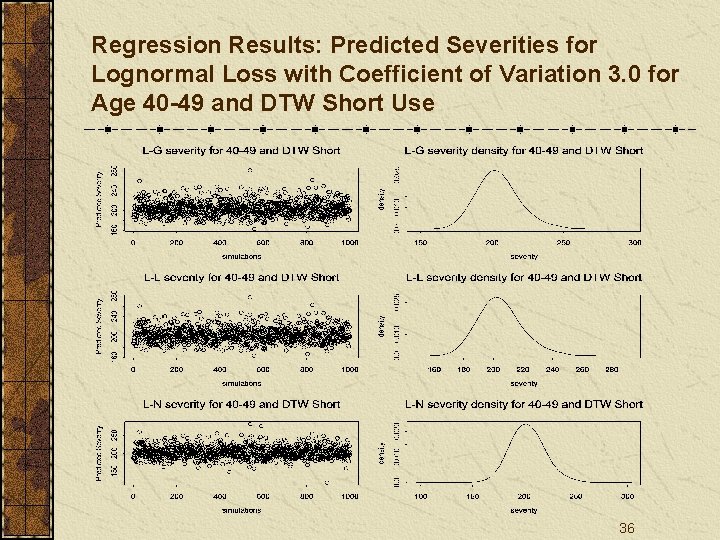
Regression Results: Predicted Severities for Lognormal Loss with Coefficient of Variation 3. 0 for Age 40 -49 and DTW Short Use 36

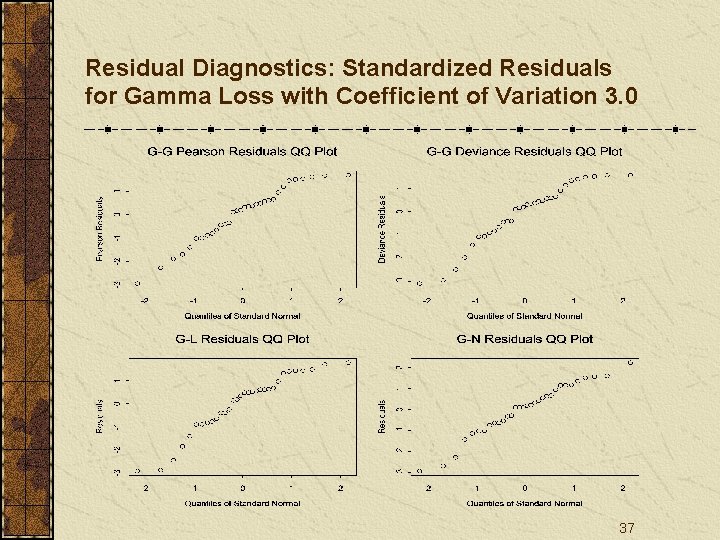
Residual Diagnostics: Standardized Residuals for Gamma Loss with Coefficient of Variation 3. 0 37

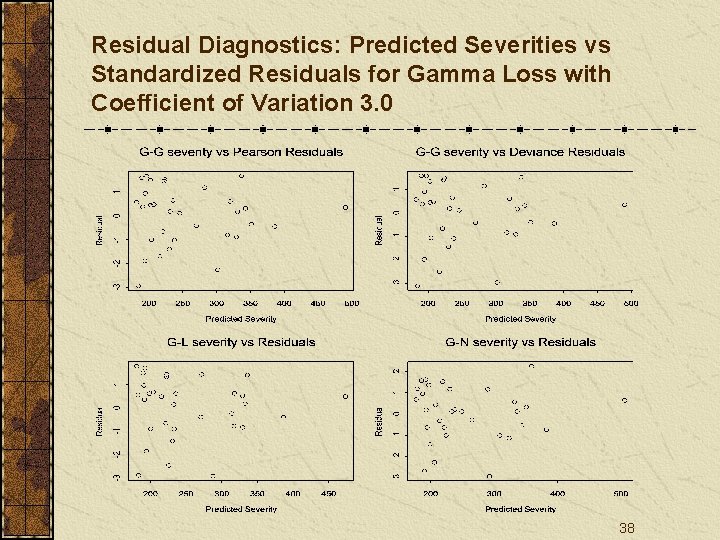
Residual Diagnostics: Predicted Severities vs Standardized Residuals for Gamma Loss with Coefficient of Variation 3. 0 38

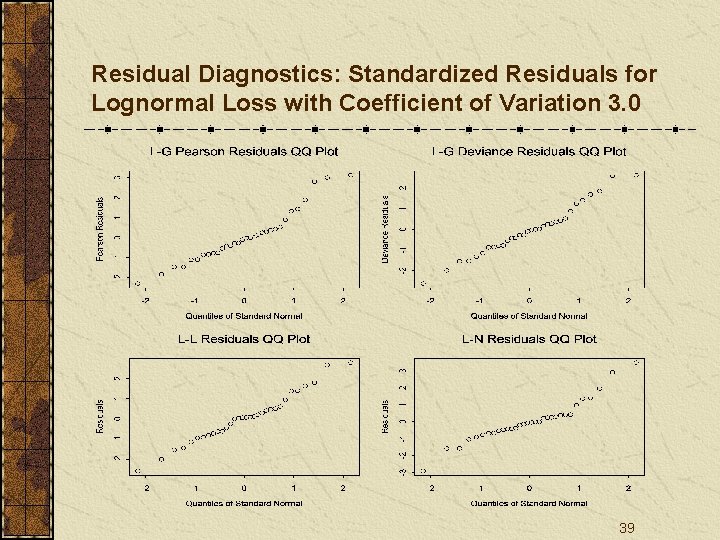
Residual Diagnostics: Standardized Residuals for Lognormal Loss with Coefficient of Variation 3. 0 39

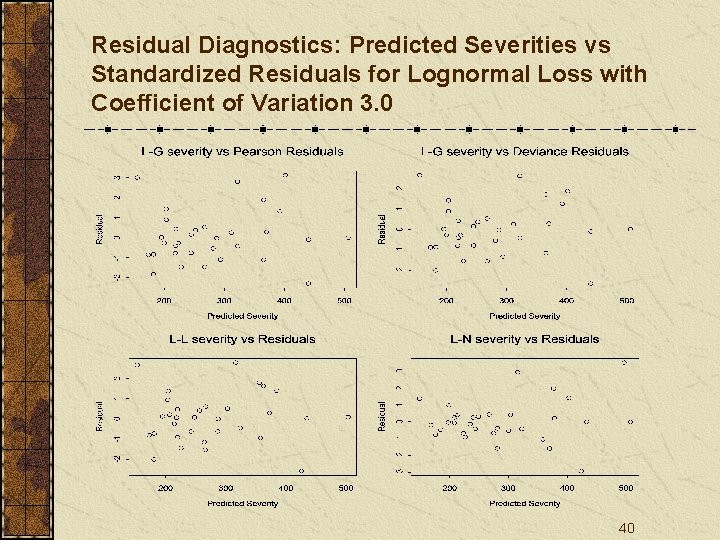
Residual Diagnostics: Predicted Severities vs Standardized Residuals for Lognormal Loss with Coefficient of Variation 3. 0 40

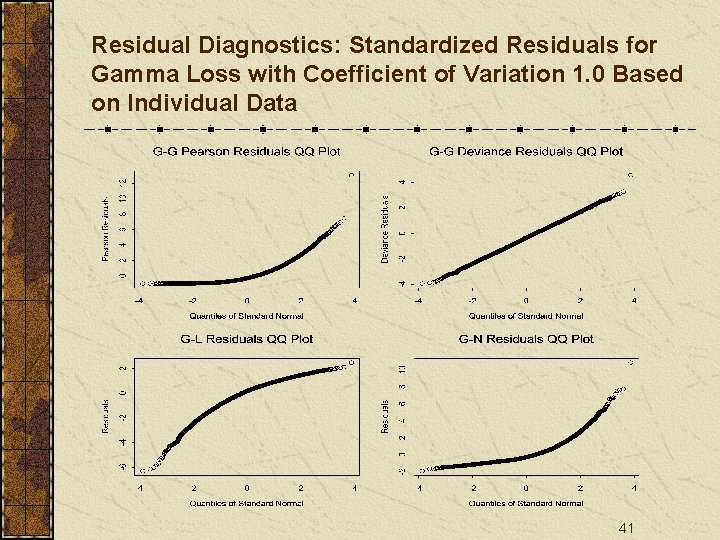
Residual Diagnostics: Standardized Residuals for Gamma Loss with Coefficient of Variation 1. 0 Based on Individual Data 41

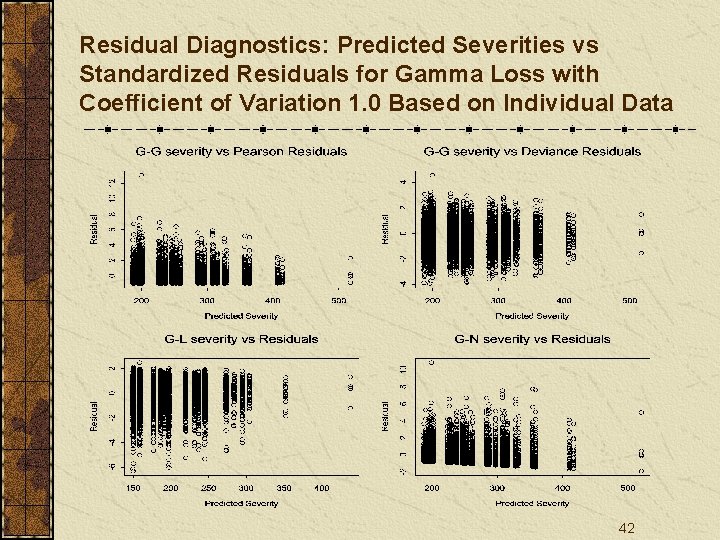
Residual Diagnostics: Predicted Severities vs Standardized Residuals for Gamma Loss with Coefficient of Variation 1. 0 Based on Individual Data 42

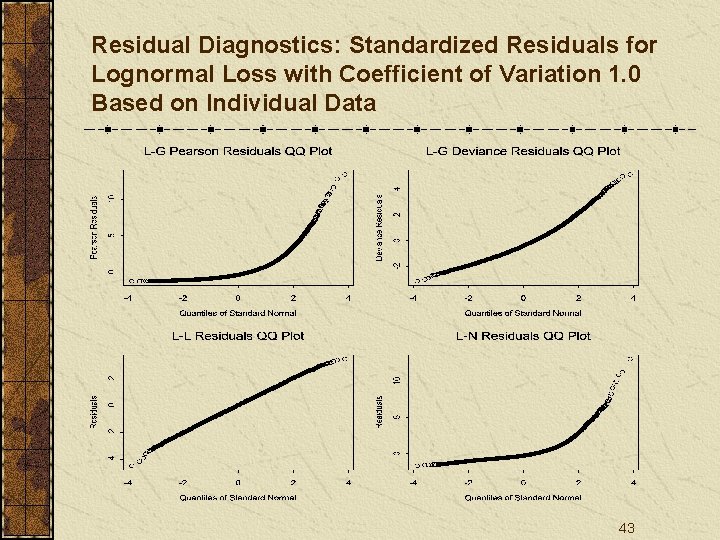
Residual Diagnostics: Standardized Residuals for Lognormal Loss with Coefficient of Variation 1. 0 Based on Individual Data 43

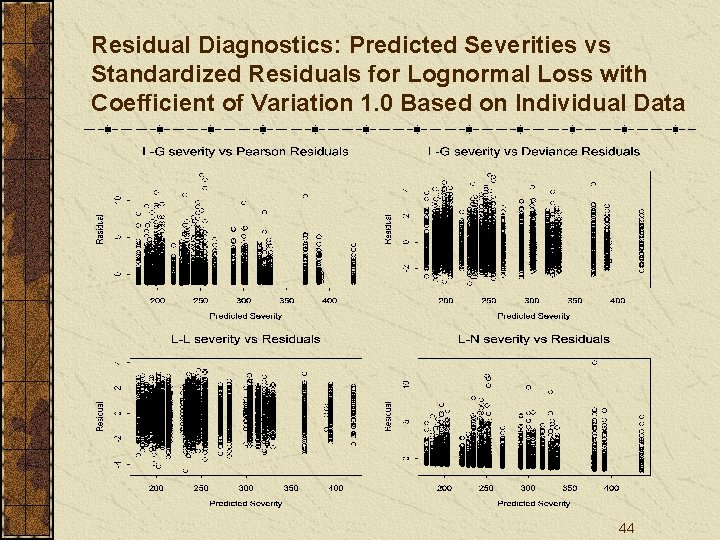
Residual Diagnostics: Predicted Severities vs Standardized Residuals for Lognormal Loss with Coefficient of Variation 1. 0 Based on Individual Data 44

Conclusions When the gamma distribution is “true”, the G-G model is dominant in both unbiasedness and stability (except the G-L model is slightly more stable in the case of large volatility). 45

Conclusions When the lognormal distribution is “true”, the L-L model is dominant in terms of stability. 46

Conclusions GLMs with a normal distribution never dominate based on any criteria, and they have the worst weighted standard error. 47

Conclusions GLMs with a gamma distribution are dominant in terms of unbiasedness, no matter whether the “true” distribution is gamma or lognormal. 48

Conclusions In general, GLMs with a gamma distribution are recommended because they perform slightly better than the log-transformed model. 49

Conclusions When the data is not volatile, the distribution selection for GLMs may not be as important because all distribution assumptions yield small biases and standard errors. 50

Conclusions When the data is very volatile, the log-transformed regression is recommended because it provides the most stable estimation. 51

Conclusions When the log-transformed model is used, the classification relativities should be adjusted by a volatility-adjustment factor. Without the adjustment, the relativities could be undervalued. 52

Conclusions Residual plots may work well to examine the distribution assumptions on individual data, but not necessarily on summarized/average data. 53

Questions & Answers Questions? Thank You! 54