Seventh Edition CHAPTER 9 VECTOR MECHANICS FOR ENGINEERS

Seventh Edition CHAPTER 9 VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University Distributed Forces: Moments of Inertia © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved.

Seventh Edition Vector Mechanics for Engineers: Dynamics Introduction The strength of structural members depends to a large extent on the properties of their cross sections, particularly on the second moments, or moments of inertia, of their areas. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 2

Seventh Edition Vector Mechanics for Engineers: Dynamics Introduction Chapter 9 – Moments of Inertia Moments of inertia are not actually used in Statics; however, since the calculations for moments of inertia are quite similar to those for centroids they are introduced at this point. Moments of inertia are used in courses such as mechanics of materials, dynamics, and fluid mechanics. The moment of inertia of an object is a measure of its resistance to change in rotation. Everyday experience tells us that it is harder to start (or stop) a large wheel turning than a small wheel. Mathematically, this is represented by the large wheel having a larger moment of inertia. Moments of inertia are used in various engineering calculations, including: • Locating the resultant of hydrostatic pressure forces on submerged bodies • Calculating stresses in beams – they are at times related to the moment of inertia of the cross-sectional area of the beam (resistance to bending) • Mass moments of inertia are used in studying the rotational motion of objects © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 3

Seventh Edition Vector Mechanics for Engineers: Dynamics Moment of Inertia (MOI) – Applications in everyday life Golf club design: © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 4

Seventh Edition Vector Mechanics for Engineers: Dynamics Moment of Inertia (MOI) Applications in everyday life Figure skating: This formula explains the speeding up of ice skaters when they pull in their arms. Since the ice is nearly frictionless, the kinetic energy should stay constant during their spin. When they pull in their arms, the skaters decrease their moment of inertia I (their mass is more concentrated close to the rotation axis). To keep the kinetic energy constant, the angular velocity ω must increase; hence, the skaters spin faster. References: Copyright 2001 -07 Physics Forums - Physics Help and Math Help. http: //www. physicsforums. com/showthread. php Here's a 564 k. B AVI movie of Paul Wylie doing a scratch spin, at 30 frames/sec. Reference: The Physics of Everyday Stuff main page. Sam Hokin / samh@fusion. kth. se © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 5

Seventh Edition Vector Mechanics for Engineers: Dynamics Introduction • We previously considered distributed forces which were proportional to the area or volume over which they act. - The resultant was obtained by summing or integrating over the areas or volumes. - The moment of the resultant about any axis was determined by computing the first moments of the areas or volumes about that axis. • We will now consider forces which are proportional to the area or volume over which they act but also vary linearly with distance from a given axis. - It will be shown that the magnitude of the resultant depends on the first moment of the force distribution with respect to the axis. - The point of application of the resultant depends on the second moment of the distribution with respect to the axis. • The current chapter will present methods for computing the moments and products of inertia for areas and masses. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 6

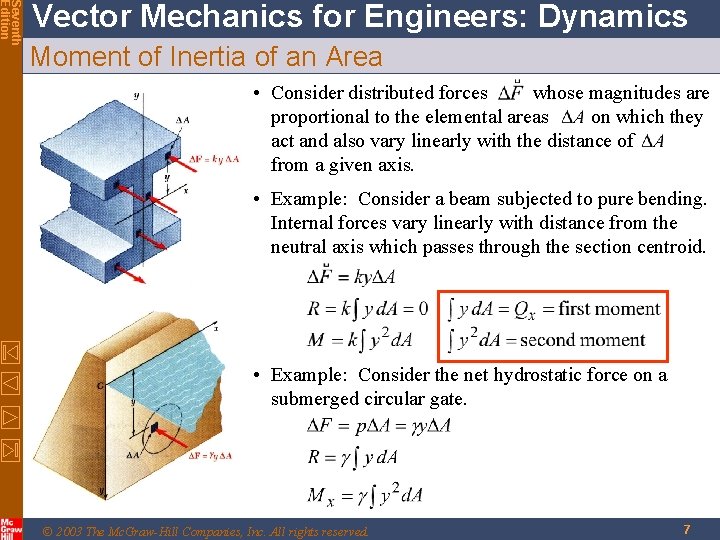
Seventh Edition Vector Mechanics for Engineers: Dynamics Moment of Inertia of an Area • Consider distributed forces whose magnitudes are proportional to the elemental areas on which they act and also vary linearly with the distance of from a given axis. • Example: Consider a beam subjected to pure bending. Internal forces vary linearly with distance from the neutral axis which passes through the section centroid. • Example: Consider the net hydrostatic force on a submerged circular gate. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 7

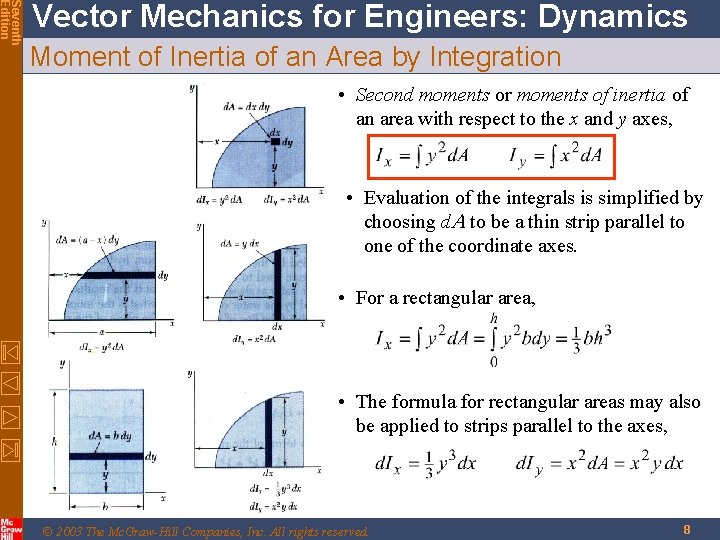
Seventh Edition Vector Mechanics for Engineers: Dynamics Moment of Inertia of an Area by Integration • Second moments or moments of inertia of an area with respect to the x and y axes, • Evaluation of the integrals is simplified by choosing d. A to be a thin strip parallel to one of the coordinate axes. • For a rectangular area, • The formula for rectangular areas may also be applied to strips parallel to the axes, © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 8

Seventh Edition Vector Mechanics for Engineers: Dynamics Polar Moment of Inertia • The polar moment of inertia is an important parameter in problems involving torsion of cylindrical shafts and rotations of slabs. • The polar moment of inertia is related to the rectangular moments of inertia, © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9

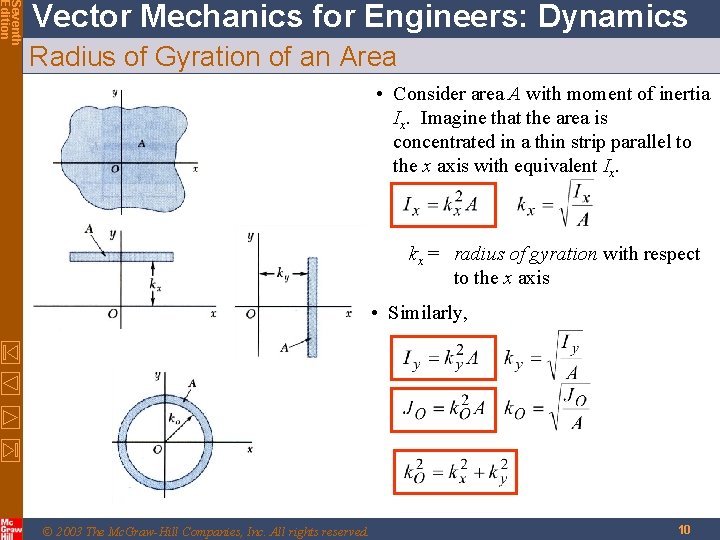
Seventh Edition Vector Mechanics for Engineers: Dynamics Radius of Gyration of an Area • Consider area A with moment of inertia Ix. Imagine that the area is concentrated in a thin strip parallel to the x axis with equivalent Ix. kx = radius of gyration with respect to the x axis • Similarly, © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 10

Seventh Edition Vector Mechanics for Engineers: Dynamics Determining moments of inertia Moments of inertia can be found using three methods: 1. Composites – If an object can be divided up into relatively simple shapes with known moments of inertia, then the moment of inertia of the entire is the sum of the moments of inertia of the composites. For N composite shapes: 2. Integration – If the area, volume, or line of an object can be described by a mathematical equations, then the moment of inertia can be determined through integration. 3. Solid modeling software – Software such as Auto. CAD can be used to construct 3 D models of objects. The software can also determine the centroid , volumes, moments of inertia and other mass properties of the object). This is not a required element of this course, but an example will be provided. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 11

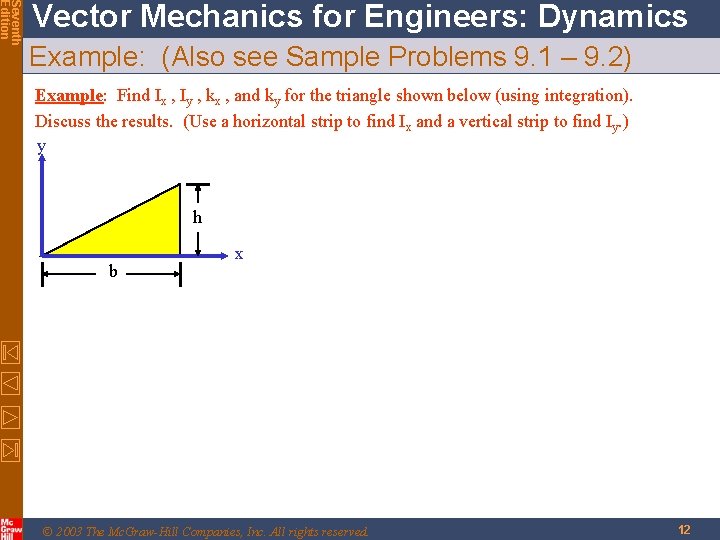
Seventh Edition Vector Mechanics for Engineers: Dynamics Example: (Also see Sample Problems 9. 1 – 9. 2) Example: Find Ix , Iy , kx , and ky for the triangle shown below (using integration). Discuss the results. (Use a horizontal strip to find Ix and a vertical strip to find Iy. ) y h b x © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 12

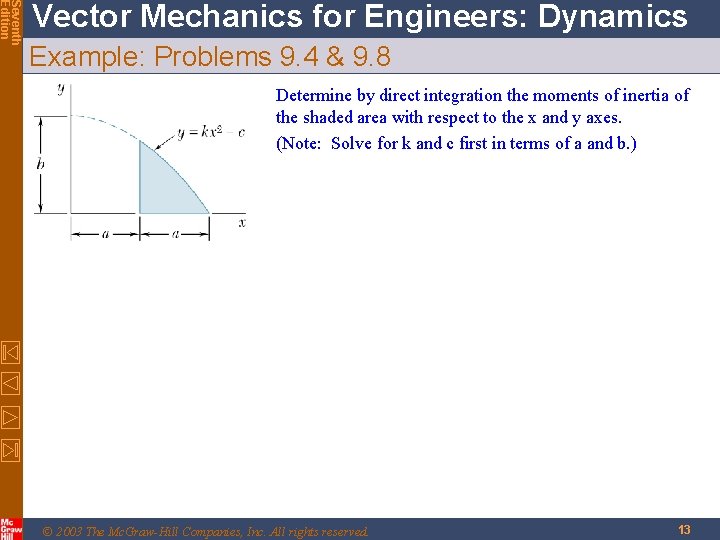
Seventh Edition Vector Mechanics for Engineers: Dynamics Example: Problems 9. 4 & 9. 8 Determine by direct integration the moments of inertia of the shaded area with respect to the x and y axes. (Note: Solve for k and c first in terms of a and b. ) © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 13

Seventh Edition Vector Mechanics for Engineers: Dynamics Parallel Axis Theorem Parallel-axis theorem Changing the axis of rotation can have a huge effect on the moment of inertia. Consider the case of trying to rotate a wheel about its axle (its centroidal axis) versus the much more difficult task of trying to rotate the wheel about a bar (axis) several feet away from the wheel. The parallel axis theorem is used to calculate the moment of inertia about a new axis if the moment of inertia about the centroidal axis is known. Important note: The parallel axis theorem shows how to find the moment of inertia about any other axis if the moment of inertia is known about the centroidal axis. So you must begin by finding the moment of inertia about the centroidal axis (i. e. , find Ix ' first to find Ix about any other axis). © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 14

Seventh Edition Vector Mechanics for Engineers: Dynamics Parallel Axis Theorem • Use the value of I for a circle from the table on the following page and the parallel-axis theorem to find IT , the moment of inertia about an axis tangent to the circle. • Use the value of IAA’ along the base of a triangle from the table on the following page and the parallel-axis theorem to find IBB’ , the moment of inertia along a parallel axis through the centroid of the triangle © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 15

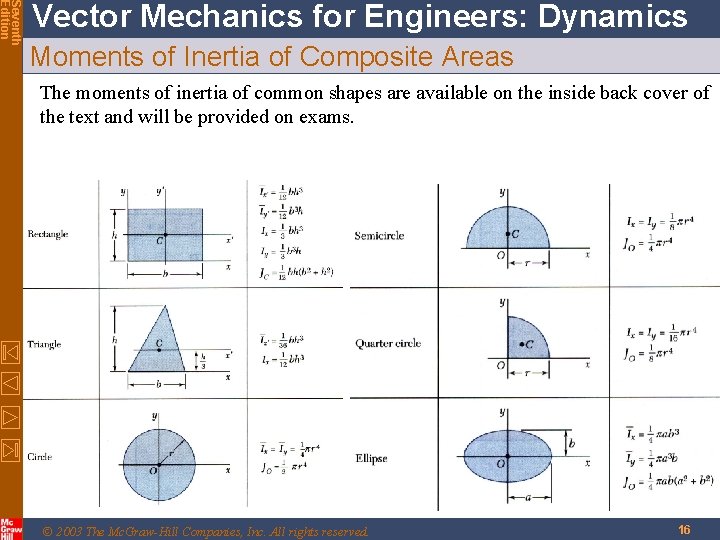
Seventh Edition Vector Mechanics for Engineers: Dynamics Moments of Inertia of Composite Areas The moments of inertia of common shapes are available on the inside back cover of the text and will be provided on exams. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 16

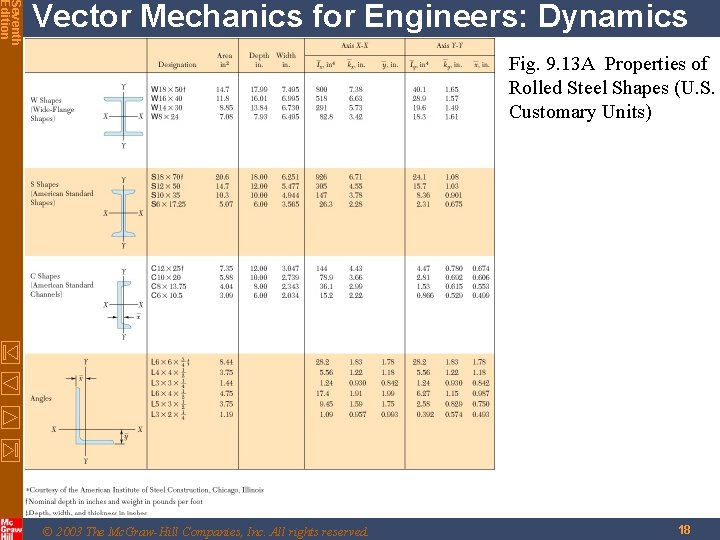
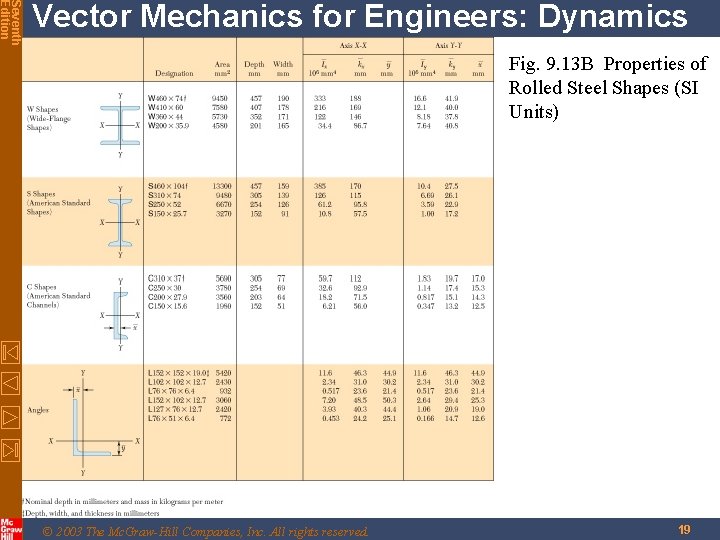
Seventh Edition Vector Mechanics for Engineers: Dynamics Moments of Inertia of Rolled-Steel Shapes Figure 9. 13 (following two pages) tabulates data for a small sample of the rolled-steel shapes that are readily available. Shown above are two examples of wide-flange shapes that are commonly used in the construction of buildings. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 17

Seventh Edition Vector Mechanics for Engineers: Dynamics Fig. 9. 13 A Properties of Rolled Steel Shapes (U. S. Customary Units) © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 18

Seventh Edition Vector Mechanics for Engineers: Dynamics Fig. 9. 13 B Properties of Rolled Steel Shapes (SI Units) © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 19

Seventh Edition Vector Mechanics for Engineers: Dynamics Demonstration: Moments of inertia Demonstration: The instructor will pass around two blocks of wood with dowels through them. Rotate the blocks using the dowels. 1) Which is easiest to rotate? 2) Where do you think that the dowel should be placed such that the block will be easiest to rotate? Why? © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 20

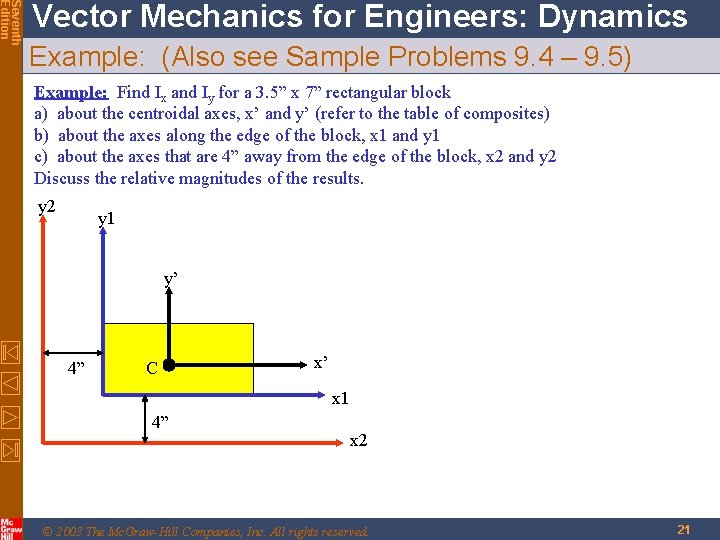
Seventh Edition Vector Mechanics for Engineers: Dynamics Example: (Also see Sample Problems 9. 4 – 9. 5) Example: Find Ix and Iy for a 3. 5” x 7” rectangular block a) about the centroidal axes, x’ and y’ (refer to the table of composites) b) about the axes along the edge of the block, x 1 and y 1 c) about the axes that are 4” away from the edge of the block, x 2 and y 2 Discuss the relative magnitudes of the results. y 2 y 1 y’ 4” C x’ x 1 4” x 2 © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 21

Seventh Edition Vector Mechanics for Engineers: Dynamics Moments of Inertia using composites Finding moments of inertia using composites: Moments of inertia are additive. If an object can be broken down into N composite shapes with known moments of inertia, then the total moment of inertia is the sum of the moments of inertia for each part. Also note that Ix and Iy are negative for negative areas. Example: The object below can be broken up into three areas with common shapes as shown. A 1 A 2 A 3 If Ix 1 and Iy 1 = the moments of inertia for area A 1 Ix 2 and Iy 2 = the moments of inertia for area A 2 Ix 3 and Iy 3 = the moments of inertia for area A 3 then Ix(total) = Ix 1 + Ix 2 + Ix 3 Iy(total) = Iy 1 + Iy 2 + Iy 3 © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 22

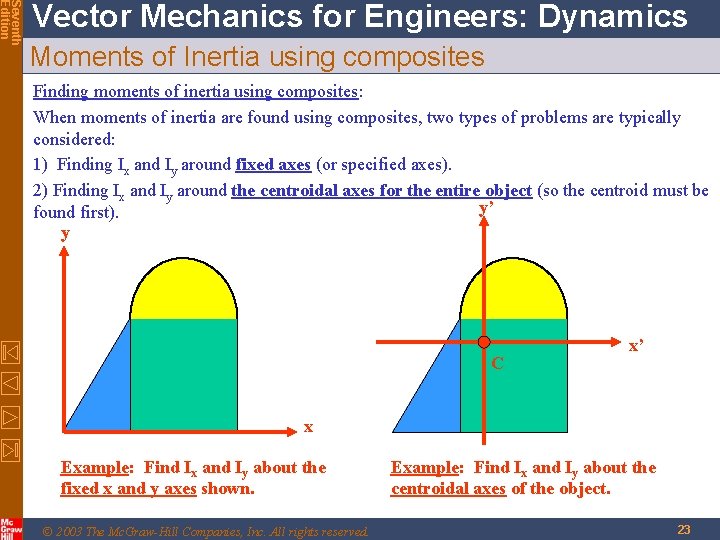
Seventh Edition Vector Mechanics for Engineers: Dynamics Moments of Inertia using composites Finding moments of inertia using composites: When moments of inertia are found using composites, two types of problems are typically considered: 1) Finding Ix and Iy around fixed axes (or specified axes). 2) Finding Ix and Iy around the centroidal axes for the entire object (so the centroid must be y’ found first). y C x’ x Example: Find Ix and Iy about the fixed x and y axes shown. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. Example: Find Ix and Iy about the centroidal axes of the object. 23

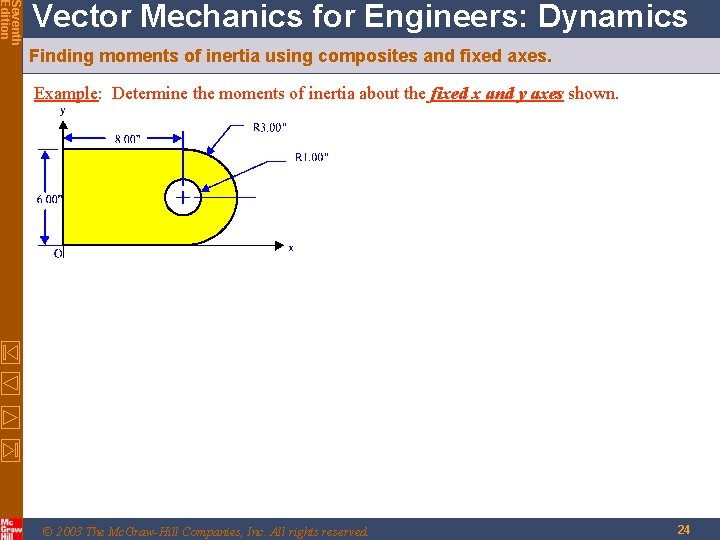
Seventh Edition Vector Mechanics for Engineers: Dynamics Finding moments of inertia using composites and fixed axes. Example: Determine the moments of inertia about the fixed x and y axes shown. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 24

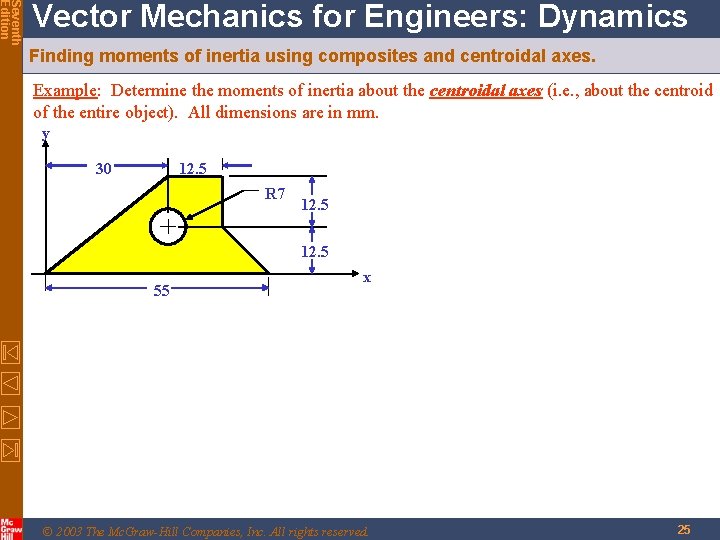
Seventh Edition Vector Mechanics for Engineers: Dynamics Finding moments of inertia using composites and centroidal axes. Example: Determine the moments of inertia about the centroidal axes (i. e. , about the centroid of the entire object). All dimensions are in mm. y 30 12. 5 R 7 12. 5 55 x © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 25

Seventh Edition Vector Mechanics for Engineers: Dynamics Example: Problem 9. 49 Two 1 -in. steel plates are welded to a rolled S section as shown. Determine the moments of inertia and the radii of gyration of the section with respect to the centroidal x and y axes. © 2003 The Mc. Graw-Hill Companies, Inc. All rights reserved. 26