Seven OClock A New Distributed GVT Algorithm using

Seven O’Clock: A New Distributed GVT Algorithm using Network Atomic Operations David Bauer, Garrett Yaun Christopher Carothers Computer Science Murat Yuksel Shivkumar Kalyanaraman ECSE
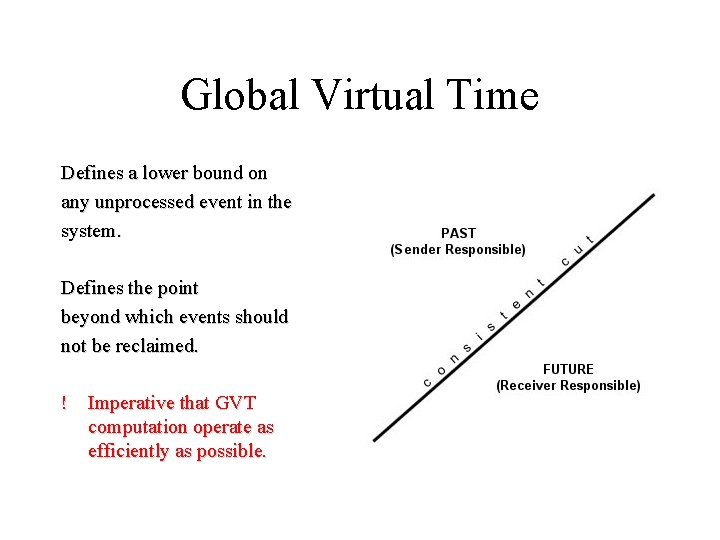
Global Virtual Time Defines a lower bound on any unprocessed event in the system. Defines the point beyond which events should not be reclaimed. ! Imperative that GVT computation operate as efficiently as possible.

Key Problems Simultaneous Reporting Problem Transient Message Problem arises “because not all processors will report their local minimum at precisely the same instant in wallclock time”. message is delayed in the network and neither the sender nor the receiver consider that message in their respective GVT calculation. Asynchronous Solution: create a synchronization, or “cut”, across the distributed simulation that divides events into two categories: past and future. Consistent Cut: a cut where there is no message scheduled in the future of the sending processor, but received in the past of the destination processor.
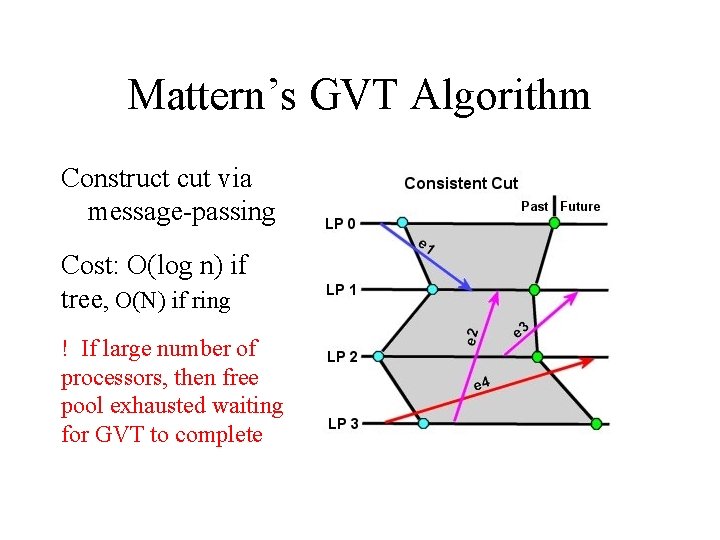
Mattern’s GVT Algorithm Construct cut via message-passing Cost: O(log n) if tree, O(N) if ring ! If large number of processors, then free pool exhausted waiting for GVT to complete
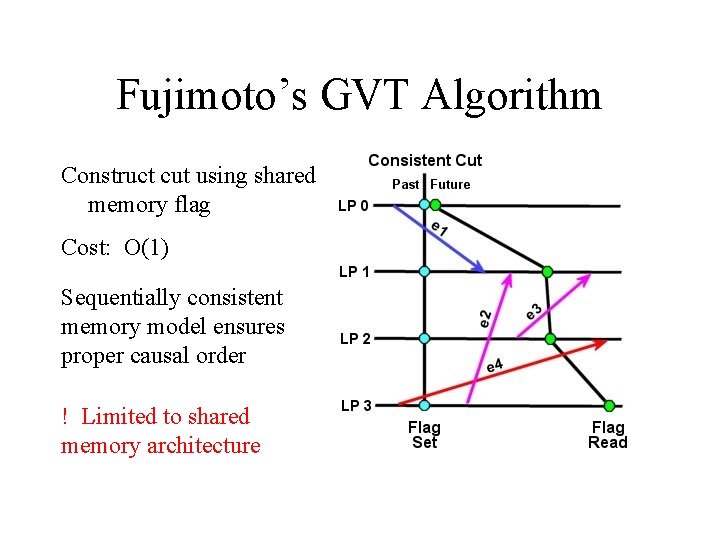
Fujimoto’s GVT Algorithm Construct cut using shared memory flag Cost: O(1) Sequentially consistent memory model ensures proper causal order ! Limited to shared memory architecture
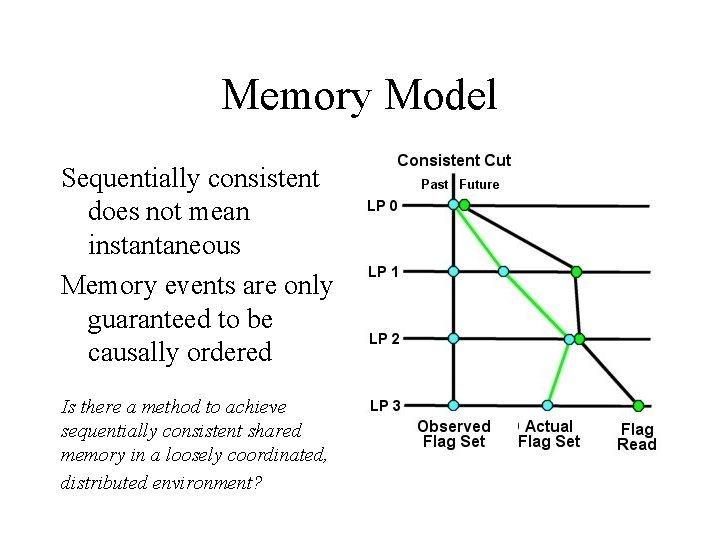
Memory Model Sequentially consistent does not mean instantaneous Memory events are only guaranteed to be causally ordered Is there a method to achieve sequentially consistent shared memory in a loosely coordinated, distributed environment?
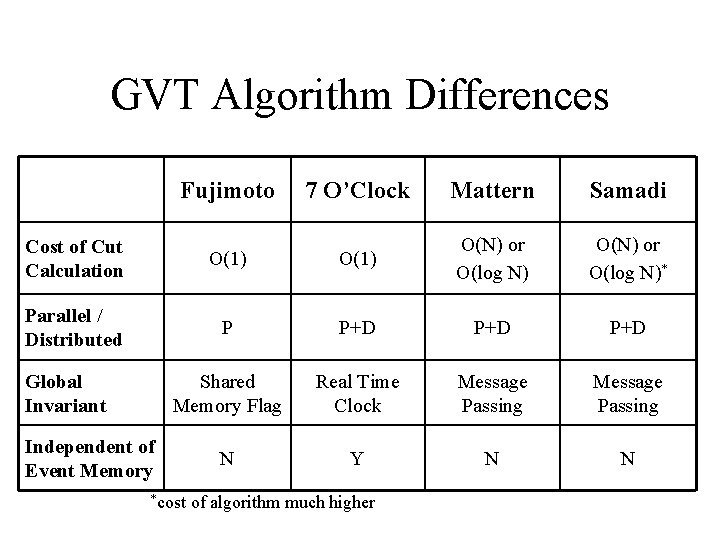
GVT Algorithm Differences Fujimoto 7 O’Clock Mattern Samadi O(N) or O(log N)* Cost of Cut Calculation O(1) O(N) or O(log N) Parallel / Distributed P P+D P+D Shared Memory Flag Real Time Clock Message Passing N Y N N Global Invariant Independent of Event Memory *cost of algorithm much higher
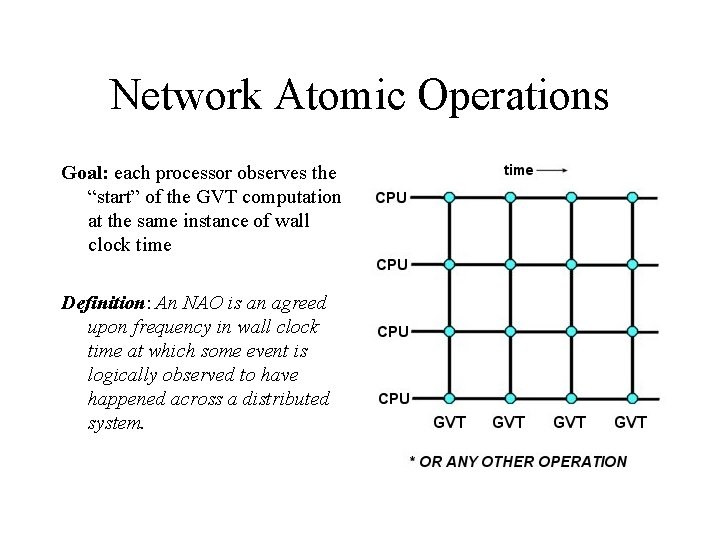
Network Atomic Operations Goal: each processor observes the “start” of the GVT computation at the same instance of wall clock time Definition: An NAO is an agreed upon frequency in wall clock time at which some event is logically observed to have happened across a distributed system.
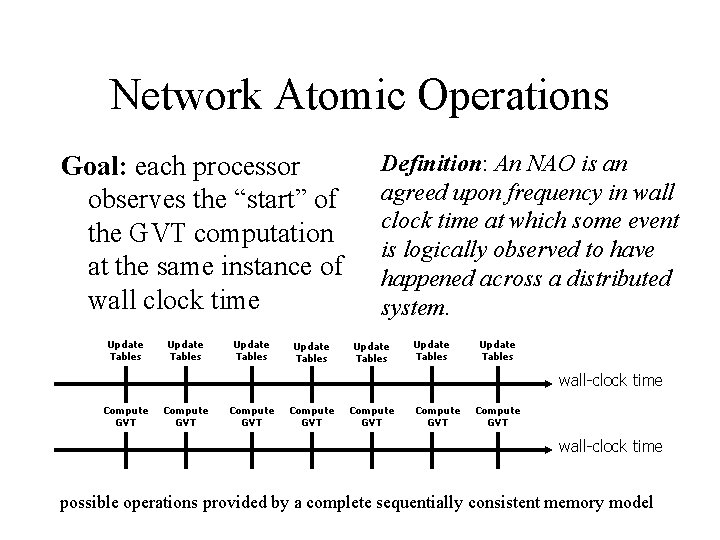
Network Atomic Operations Goal: each processor observes the “start” of the GVT computation at the same instance of wall clock time Update Tables Definition: An NAO is an agreed upon frequency in wall clock time at which some event is logically observed to have happened across a distributed system. Update Tables wall-clock time Compute GVT Compute GVT wall-clock time possible operations provided by a complete sequentially consistent memory model

Clock Synchronization • Assumption: all processors share a highly accurate, common view of wall clock time. • Basic building block: CPU timestamp counter – Measures time in terms of clock cycles, so a gigahertz CPU clock has granularity of 109 secs – Sending events across network is much larger granularity depending on tech: ~106 secs on 1000 base/T

Clock Synchronization • Issues: clock synchronization, drift and jitter • Ostrovsky and Patt-Shamir: – provably optimal clock synchronization – clocks have drift and the message latency may be unbounded • Well researched problem in distributed computing – we used simplified approach – simplified approach helpful in determining if system working properly

Max Send t • Definition: max_send_delta_t is maximum of – worst case bound on the time to send an event through the network – twice synchronization error – twice max clock drift over simulation time • add a small amount of time to the NAO expiration – Similar to sequentially consistent memory • Overcomes: – Transient message problem, clock drift/jitter and clock synchronization error

Max Send t: clock drift • Clock drift causes CPU clocks to become unsynchronized – Long running simulations may require multiple synchs – Or, we account for it in the NAO • Max Send t overcomes clock drift by ensuring no event “falls between the cracks”

Max Send t • What if clocks are not well synched? – Let Dmax be the maximum clock drift. – Let Smax be the maximum synchronization error. • Solution: Re-define tmax as tmax Dmax GVT LP 2 t’max = max( tmax , 2* Dmax , 2* Smax) • In practice both Dmax and Smax are very LP 1 small in comparison to tmax Dmax GVT wallclock time

Transient Message Problem • Max Send t: worst case bound on time to send event in network – guarantees events are accounted for by either sender of receiver

Simultaneous Reporting Problem • Problem arises when processors do not start GVT computation simultaneously • Seven O’Clock does start simultaneously across all CPUs, therefore, problem cannot occur
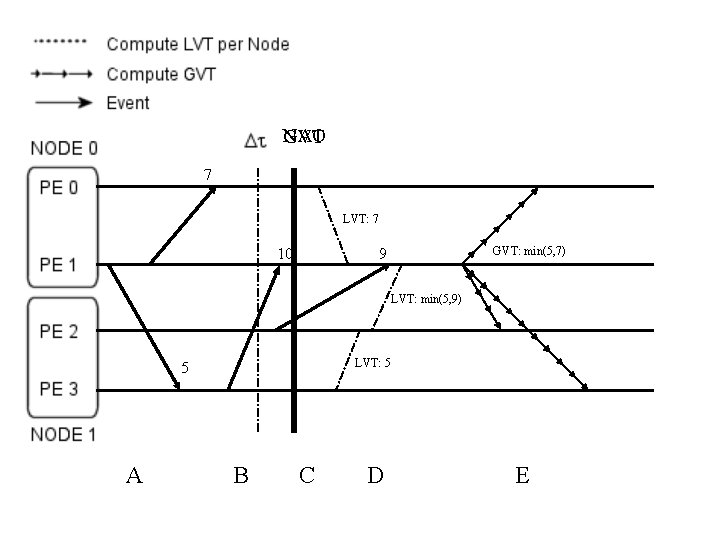
NAO GVT 7 LVT: 7 10 GVT: min(5, 7) 9 LVT: min(5, 9) LVT: 5 5 A B C D E
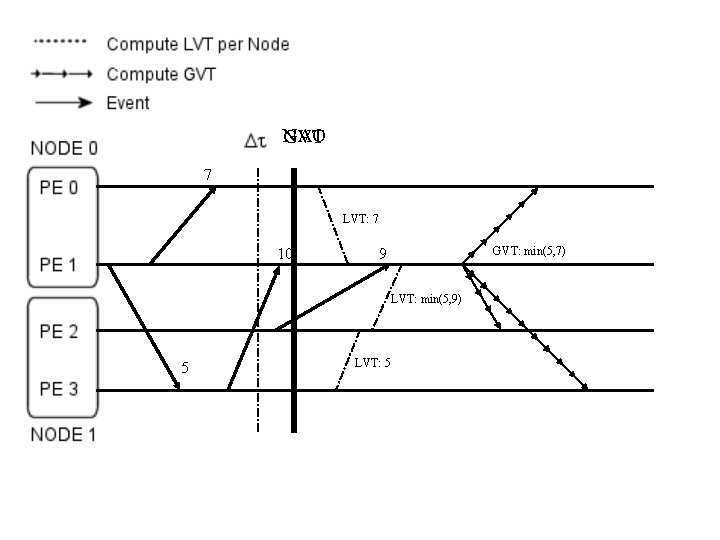
NAO GVT 7 LVT: 7 10 GVT: min(5, 7) 9 LVT: min(5, 9) 5 LVT: 5
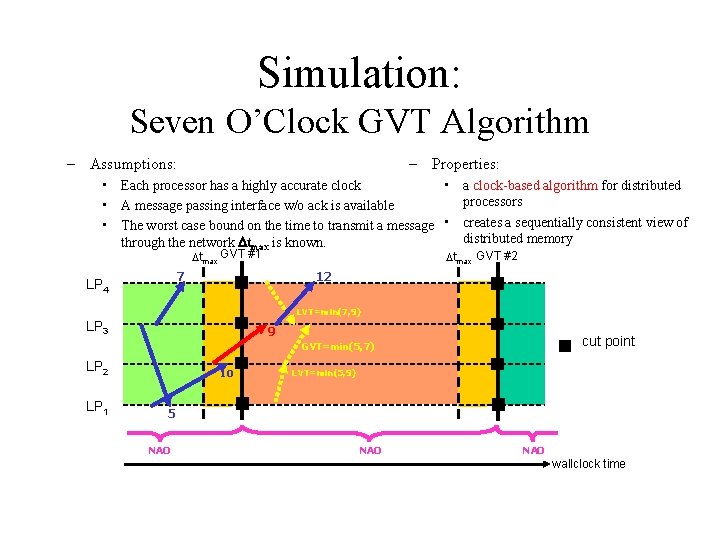
Simulation: Seven O’Clock GVT Algorithm – Assumptions: – Properties: • Each processor has a highly accurate clock • a clock-based algorithm for distributed processors • A message passing interface w/o ack is available • The worst case bound on the time to transmit a message • creates a sequentially consistent view of distributed memory through the network tmax is known. tmax GVT #1 tmax GVT #2 7 LP 4 12 LVT=min(7, 9) LP 3 9 cut point GVT=min(5, 7) LP 2 LP 1 10 LVT=min(5, 9) 5 NAO NAO wallclock time

Limitations • NAOs cannot be “forced” – agreed upon intervals cannot change • Simulation End Time – worst-case, complete NAO and only one event remaining to process – amortized over entire run-time, cost is O(1) • Exhausted Event Pool – requires tuning to ensure enough optimistic memory available

Uniqueness • Only real-time based GVT algorithm • Zero-cost consistent-cut truly scalable – O(1) cost optimal • Only algorithm which is entirely independent of available event memory – Event memory loosely tied to GVT algorithm

Performance Analysis: Models r-PHOLD • PHOLD with reverse computation • Modified to control percent remote events (normally 75%) • Destinations still decided using a uniform random number generator all LPs possible destination TCP-Tahoe • TCP-TAHOE ring of Campus Networks topology • Same topology design as used by PDNS in MASCOTS ’ 03 • Model limitations required us to increase the number of LAN routers in order to simulate the same network
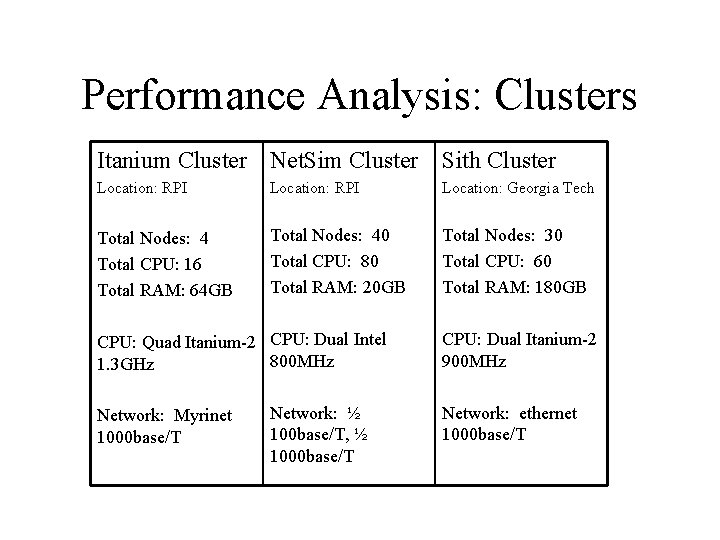
Performance Analysis: Clusters Itanium Cluster Net. Sim Cluster Sith Cluster Location: RPI Location: Georgia Tech Total Nodes: 4 Total CPU: 16 Total RAM: 64 GB Total Nodes: 40 Total CPU: 80 Total RAM: 20 GB Total Nodes: 30 Total CPU: 60 Total RAM: 180 GB CPU: Quad Itanium-2 CPU: Dual Intel 800 MHz 1. 3 GHz Network: Myrinet 1000 base/T Network: ½ 100 base/T, ½ 1000 base/T CPU: Dual Itanium-2 900 MHz Network: ethernet 1000 base/T
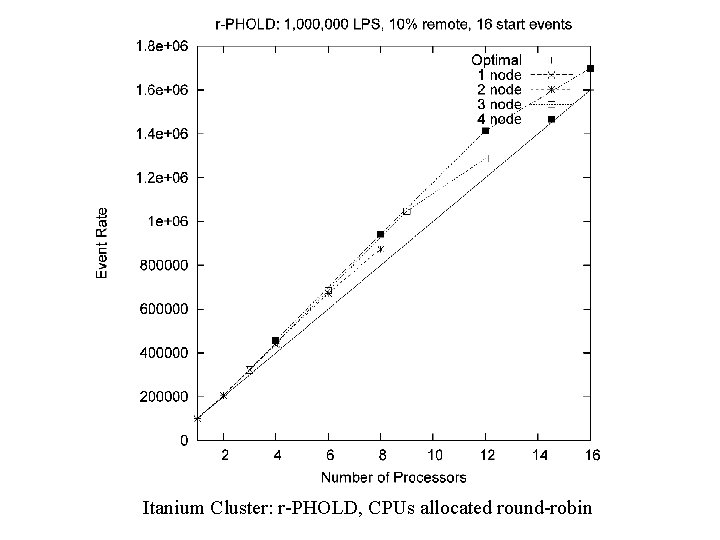
Itanium Cluster: r-PHOLD, CPUs allocated round-robin
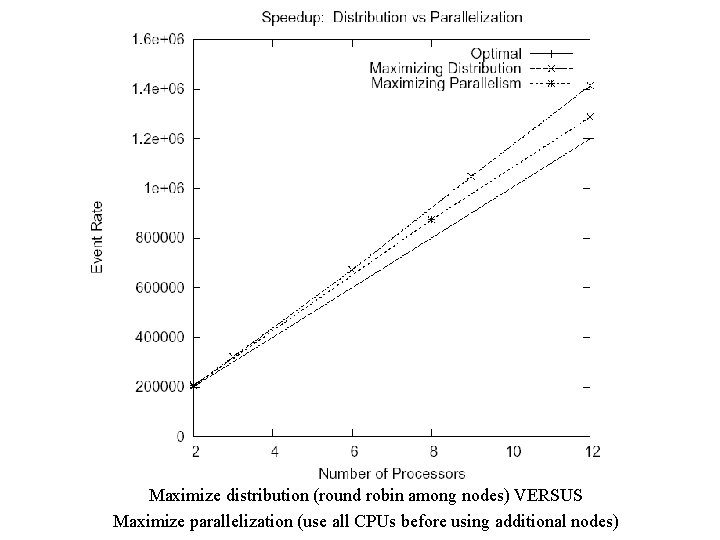
Maximize distribution (round robin among nodes) VERSUS Maximize parallelization (use all CPUs before using additional nodes)
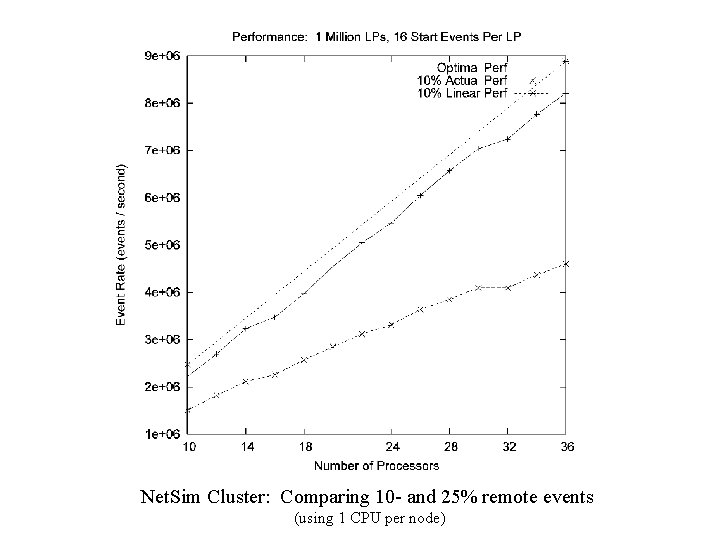
Net. Sim Cluster: Comparing 10 - and 25% remote events (using 1 CPU per node)
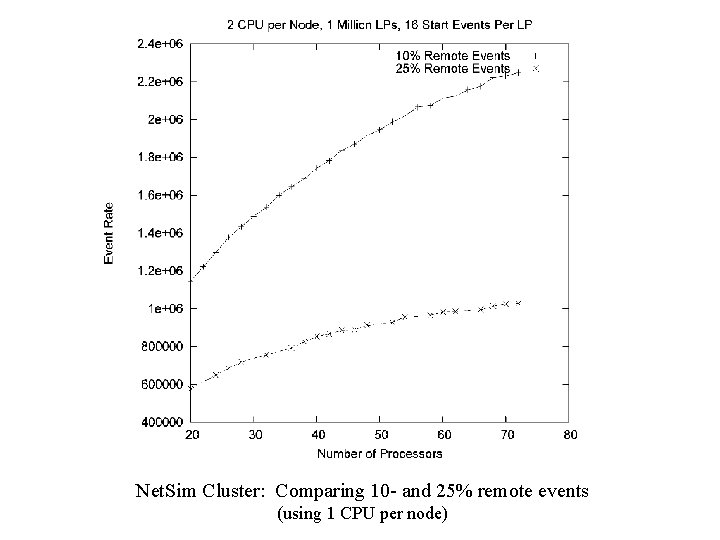
Net. Sim Cluster: Comparing 10 - and 25% remote events (using 1 CPU per node)
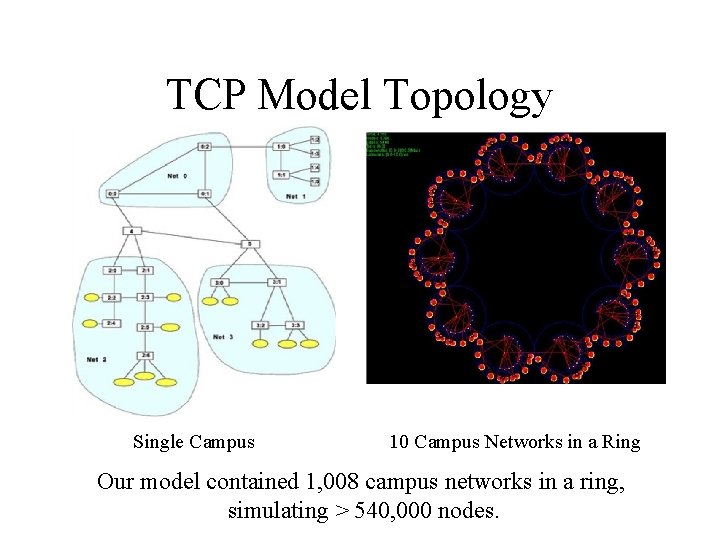
TCP Model Topology Single Campus 10 Campus Networks in a Ring Our model contained 1, 008 campus networks in a ring, simulating > 540, 000 nodes.
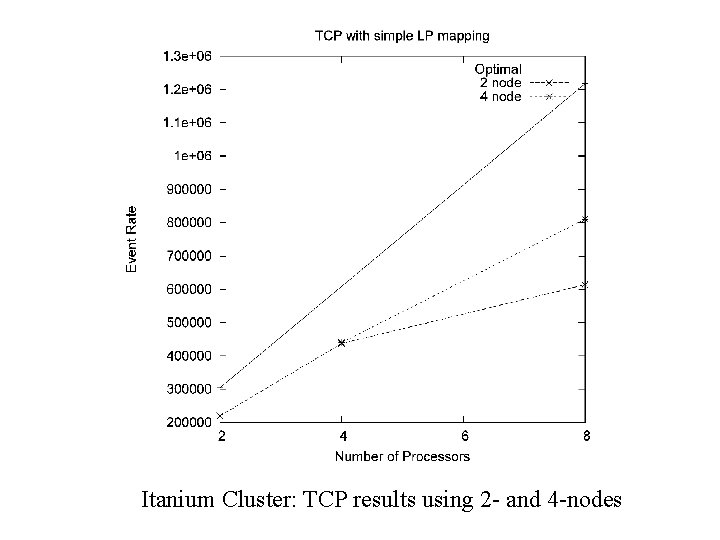
Itanium Cluster: TCP results using 2 - and 4 -nodes
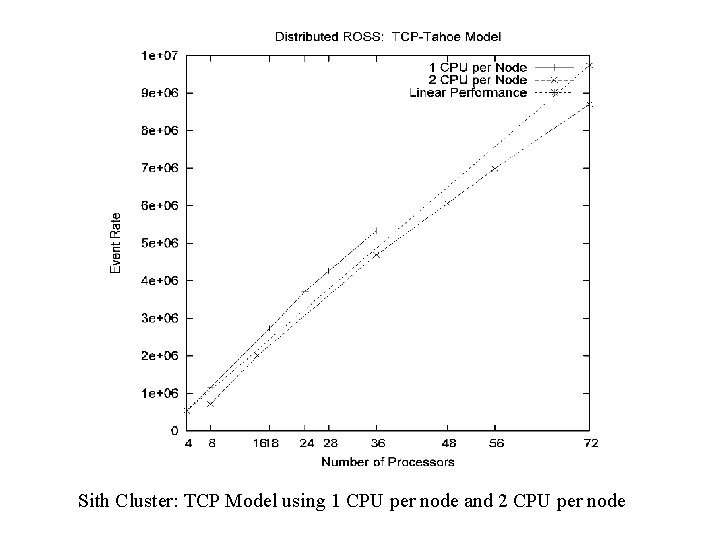
Sith Cluster: TCP Model using 1 CPU per node and 2 CPU per node

Future Work & Conclusions • Investigate “power” of different models by computing spectral analysis – GVT now in frequency domain – Determine max length of rollbacks • Investigate new ways of measuring performance – Models too large to run sequentially – Account for hardware affects (even in NOW there are fluctuations in HW performance) – Account for model LP mapping – Account for different cases, ie, 4 CPUs distributed across 1, 2, and 4 nodes
- Slides: 31