Setting the Stage for Students Conceptual Change in

Setting the Stage for Students’ Conceptual Change in Learning Statistics CAUSE Webinar June, 2008 Bob Del. Mas University of Minnesota Marsha Lovett Carnegie Mellon University College of Education and Human Development University of Minnesota

Main Premise • Much of student learning is driven by relatively few basic learning mechanisms • An effective course/lesson creates the conditions in which these learning mechanisms work together to support the learning goals we have set for our students College of Education and Human Development University of Minnesota

Learning Principle #1 • New knowledge is acquired through the lens of prior knowledge Students see things differently from the way we do What we intuitively feel will foster learning may not even be understood by students (This is called the expert blindspot) College of Education and Human Development University of Minnesota

Implications • Students often do not know: What features are important to attend to? How to find what is important in a problem, situation, question? Which situations are similar to each other in important ways? What ideas or concepts should be distinguished? College of Education and Human Development University of Minnesota

Illustration: Two Sides of the Elephant Students don’t always see things the way we do Okay, get this thing to look something like x = 4. Find the set of values which may be substituted for x and which make the statement true. Huh? ? There’s no answer!!! Solve for x Good, he’s shown that the statement is true no matter the value of x. College of Education and Human Development University of Minnesota

Illustration: Statistics Problems • Data-analysis problems involve lots of details and realworld issues • Experts know what to attend to, e. g. , variables measured, study design, possible confounds, etc. • Students may attend to other aspects, e. g. , cover story, how the question is phrased, number of variables presented College of Education and Human Development University of Minnesota

Instructional Strategies • Give students explicit direction about what features are important and what they should attend to • Give students practice identifying (and explaining) what is important Gradually build up the complexity of problems so students are not overwhelmed with too much information at once College of Education and Human Development University of Minnesota

Learning Principle #2 • The way students organize knowledge determines how they use it Just as prior knowledge influences how new knowledge is interpreted, the organization of new knowledge influences how it is used • Instructional strategies: Helping students see the connections and relationships – both in new knowledge and between old and new - will create more links for effective retrieval College of Education and Human Development University of Minnesota

Learning Principle #3 • Learners refine their knowledge and skills with timely feedback and subsequent opportunities to practice Without feedback, students often do not know their own gaps and inaccuracies Without additional opportunities to practice, they cannot strengthen their refined knowledge and skill College of Education and Human Development University of Minnesota

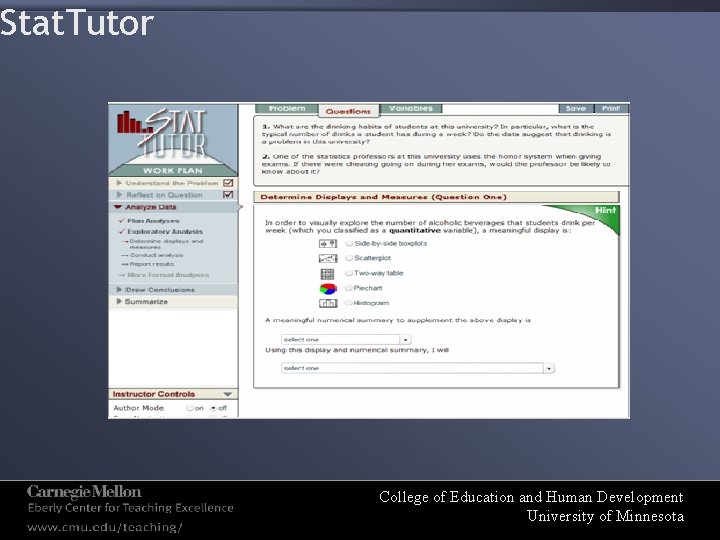
Illustration: Stat. Tutor Feedback • As compared to a traditional statistics lab assignment, where feedback comes days after the error was made, Stat. Tutor alerts students when they have made an error and offers multiple levels of feedback College of Education and Human Development University of Minnesota

Stat. Tutor College of Education and Human Development University of Minnesota

Instructional Strategies • Look for where you can give students feedback on key skills they are practicing • Look for how to make the feedback timely • Look for opportunities for students to get extra practice on the skills where they received feedback College of Education and Human Development University of Minnesota

Learning Principle #4 • Meaningful engagement is necessary for deeper learning Applying what they have learned is one way to get students actively engaged with the material Authentic practice motivates students and focuses their effort on important aspects of the task • Statistics examples and strategies Students work on projects (often in groups) Students do activities in class (e. g. , collecting data, running physical simulations) College of Education and Human Development University of Minnesota

Main Premise • Much of student learning is driven by relatively few basic learning mechanisms • An effective course/lesson creates the conditions in which these learning mechanisms work together to support the learning goals we have set for our students College of Education and Human Development University of Minnesota

Adapting and Implementing Innovative Materials in Statistics: The AIMS Curriculum • Transform an introductory statistics course into one that implements the Guidelines for Assessment and Instruction in Statistics Education (GAISE) (http: //www. amstat. org/education/gaise/) • Use research-based design principles to adapt innovative instructional materials (Cobb & Mc. Clain, 2004). College of Education and Human Development University of Minnesota

Research Basis for Lesson • • • Use of simulation throughout course Revisit concepts throughout course Informal to formal ideas of sampling Making and testing conjectures Simulation of Samples (SOS) Model: Organizational scheme to support abstraction of important concepts across simulations College of Education and Human Development University of Minnesota

Outline of a Lesson • • • Statement of a Research Question Whole class discussion Activity 1 • • Activity 2: Repeat cycle Wrap Up: Discussion and Summary of Main Ideas § Students work in small groups, make conjectures § Generate or Simulate data § Small group discussion of results § Whole class discussion College of Education and Human Development University of Minnesota

Sample Lesson: Reese’s Pieces • • Part of Unit on Sampling and Sampling Variability • Initial whole class discussion : Adapted from Rossman and Chance Workshop Statistics § If I get only five orange Reese’s Pieces in a cup of 25 candies, should I be surprised? § Out of 100, how many Yellow, Orange, Blue? § Conjecture: Expected count for Orange for each of 10 random samples, n = 25 College of Education and Human Development University of Minnesota

Each student group takes a random sample of n = 25 Separates and counts each color Then calculates and records proportion of Orange College of Education and Human Development University of Minnesota

Instructor creates dotplot of sample proportions Students work in small groups to answer questions • Did everyone have the same proportion of orange candies? • Describe the variability of this distribution of sample proportions in terms of shape, center, and spread. • Do you know the proportion of orange candies in the population? In the sample? • Which one can we always calculate? Which one do we have to estimate? • Based on the distribution, what would you ESTIMATE to be the population parameter, the proportion of orange Reese’s Pieces candies produced by Hershey's Company? • What if everyone in the class only took 10 candies? What if everyone in the class each took 100 candies? Would the distribution change? College of Education and Human Development University of Minnesota

Activity with Reese’s Pieces Applet http: //www. rossmanchance. com/applets/Reeses. Pieces. html Students work in groups of 3 to 4 to run the simulation, answer questions, and make and test conjectures: How does this compare to the dot plot on the board? Where does 0. 2 fall? Where does 0. 7 fall? [Informal idea of p-value] Conjecture what will happen if we change to n = 10? n = 100? Run the simulations to check your conjectures. College of Education and Human Development University of Minnesota

Three dotplots For each sample size (n=10, n=25, n=100), how close is the mean sample statistic (mean proportion), to the population parameter? • As the sample size increases, what happens to the distance the sample statistics are from the population parameter? • Describe the effect of sample size on the distribution of sample statistics in terms of shape, center and spread. • College of Education and Human Development University of Minnesota

Identifying the Important Parts & Immediate Feedback POPULATION Distribution of Sample Statistics Each time we do a simulation, we want to make sure we know what each part of the simulation represents. Can you identify: The Population? SAMPLE The Population Parameter? STATISTIC The Sample? The Sample Statistic? PARAMETER The Distribution of Sample Statistics? College of Education and Human Development University of Minnesota

Simulation of Samples (SOS) Model College of Education and Human Development University of Minnesota

More Practice with Follow Up Activities • Next day: simulations of sampling coins, words • Students discover the predictable pattern • Third day: Students “Discover” the central limit theorem” using stickers and Sampling SIM software College of Education and Human Development University of Minnesota

Remember that. . . It’s not teaching that causes learning. Attempts by the learner to perform cause learning, dependent upon the quality of feedback and opportunities to use it (Grant Wiggins, 1993). College of Education and Human Development University of Minnesota

AIMS Lessons, Lessons Plans, and Materials will be available at the end of summer 2008 at: http: //www. tc. umn. edu/~aims/ More information on Principles of Learning available at: http: //www. cmu. edu/teaching/principles/learning. html Reference Cobb, P. & Mc. Clain, K. (2004). Principles of instructional design for supporting the development of students’ statistical reasoning. In D. Ben-Zvi and J. Garfield (Eds. ), The Challenge of Developing Statistical Literacy, Reasoning, and Thinking (pp. 375 -395). Dordrecht, The Netherlands: Kluwer Academic Publishers. College of Education and Human Development University of Minnesota