Sets With Notation Demonstration This resource provides animated

Sets – With Notation – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

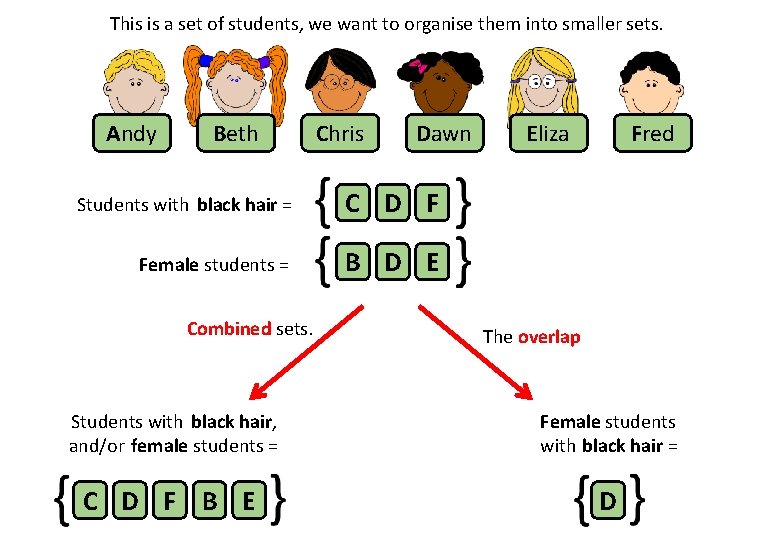
This is a set of students, we want to organise them into smaller sets. Andy Beth Chris Dawn Students with black hair = C D F Female students = B D E Combined sets. Eliza Fred The overlap Students with black hair, and/or female students = Female students with black hair = C D F B E D

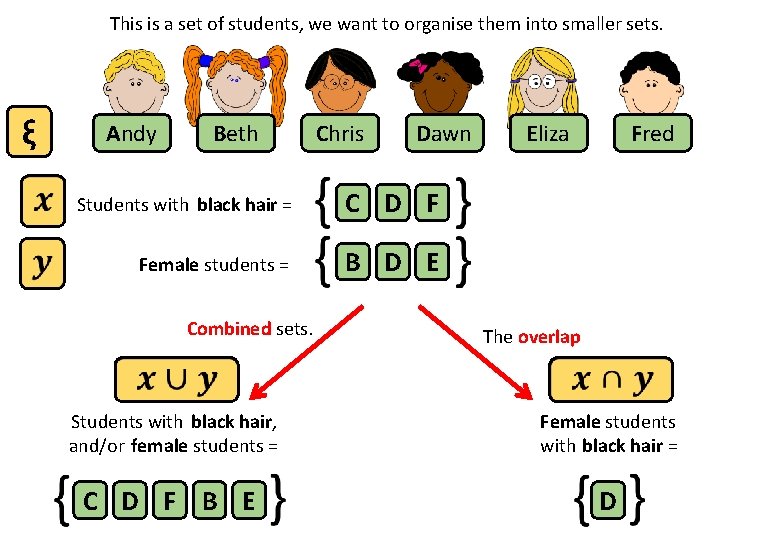
This is a set of students, we want to organise them into smaller sets. ξ Andy Beth Chris Dawn Students with black hair = C D F Female students = B D E Combined sets. Eliza Fred The overlap Students with black hair, and/or female students = Female students with black hair = C D F B E D

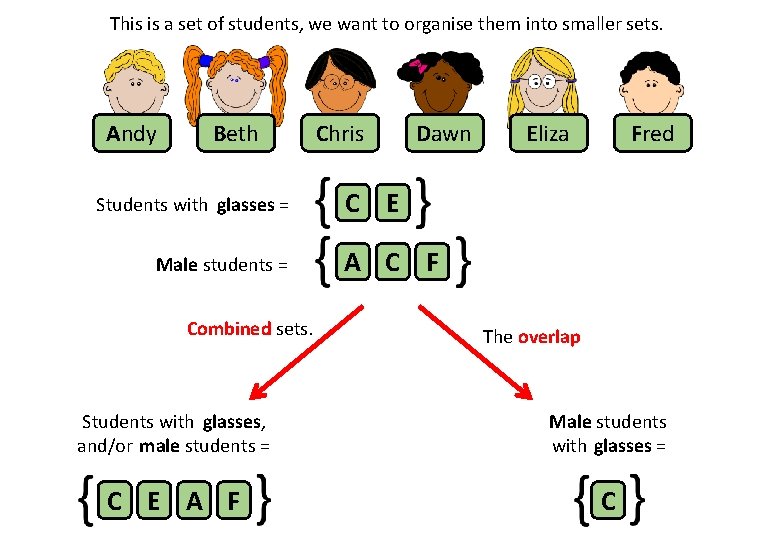
This is a set of students, we want to organise them into smaller sets. Andy Beth Students with glasses = Male students = Combined sets. Chris Dawn Eliza Fred C E A C F The overlap Students with glasses, and/or male students = Male students with glasses = C E A F C

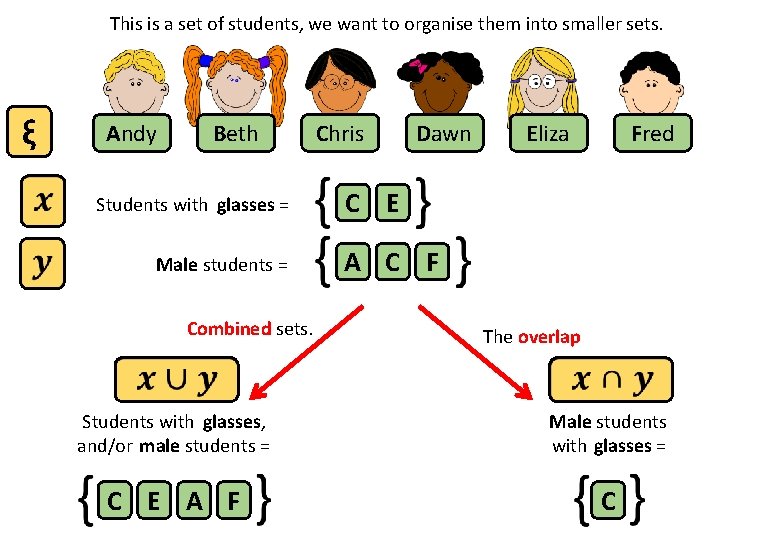
This is a set of students, we want to organise them into smaller sets. ξ Andy Beth Students with glasses = Male students = Combined sets. Chris Dawn Eliza Fred C E A C F The overlap Students with glasses, and/or male students = Male students with glasses = C E A F C

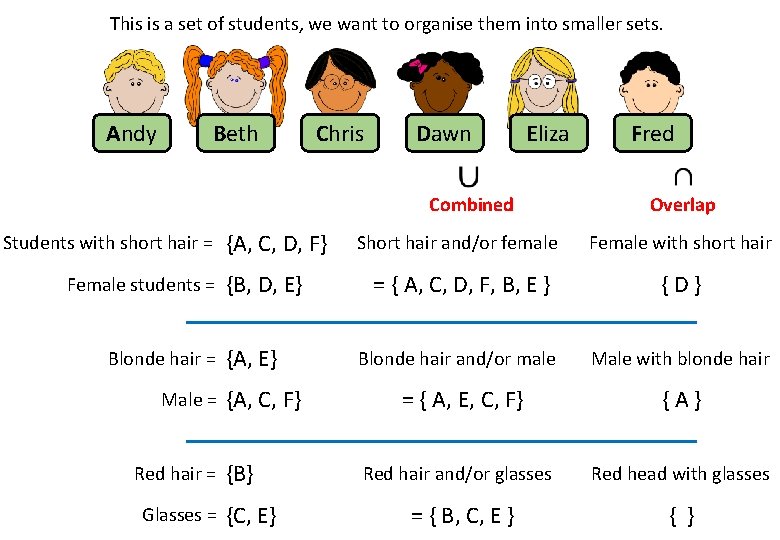
This is a set of students, we want to organise them into smaller sets. Andy Beth Chris Dawn Eliza Combined Students with short hair = Female students = Blonde hair = Male = Red hair = Glasses = {A, C, D, F} {B, D, E} {A, C, F} {B} {C, E} Fred Overlap Short hair and/or female Female with short hair = { A, C, D, F, B, E } {D} Blonde hair and/or male Male with blonde hair = { A, E, C, F} {A} Red hair and/or glasses Red head with glasses = { B, C, E } { }

Set Notation Universal Sets of Data ξ = {Numbers 1 to 20 inclusive} Elements A = {Square Numbers} = {1, 4, 9, 16} What is… B = {Multiples of 4} = {4, 8, 12, 16, 20} A ∪ B Union: the combination of A and B. A ∪ B = {1, 4, 8, 9, 12, 16, 20} A ∩ B Intersection: The overlap of A and B. A ∩ B = {4, 16} A’ Complement: Not in A. A’ = {2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20}

A ∪ B Union: the combination of A and B. A ∩ B Intersection: The overlap of A and B. A’ Complement: Not in A. ξ = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } A = { Multiples of 2 } = { 2, 4, 6, 8 } B = { Square numbers } = { 1, 4, 9 } A ∪ B = A ∩ B = B’ = { 2, 4, 6, 8, 1, 9 } {4} { 2, 3, 4, 5, 6, 7, 8 }

A ∪ B Union: the combination of A and B. A ∩ B Intersection: The overlap of A and B. A’ Complement: Not in A. ξ = { 10 to 20 inclusive } A = { Multiples of 5 } = { 10, 15, 20 } B = { Multiples of 4 } = { 12, 16, 20 } A ∪ B = A ∩ B = B’ = { 10, 15, 20, 12, 16 } { 20 } { 10, 11, 13, 14, 15, 17, 18, 19 }

A ∪ B Union: the combination of A and B. A ∩ B Intersection: The overlap of A and B. A’ Complement: Not in A. ξ = { 1 to 12 inclusive } A = { Factors of 24 } = { 1, 2, 3, 4, 6, 8, 12 } B = { Multiples of 3} = { 3, 6, 9, 12 } A ∪ B = A ∩ B = A’ = { 1, 2, 3, 4, 6, 8, 12, 9 } { 3, 6, 12 } { 5, 7, 9, 10, 11 }

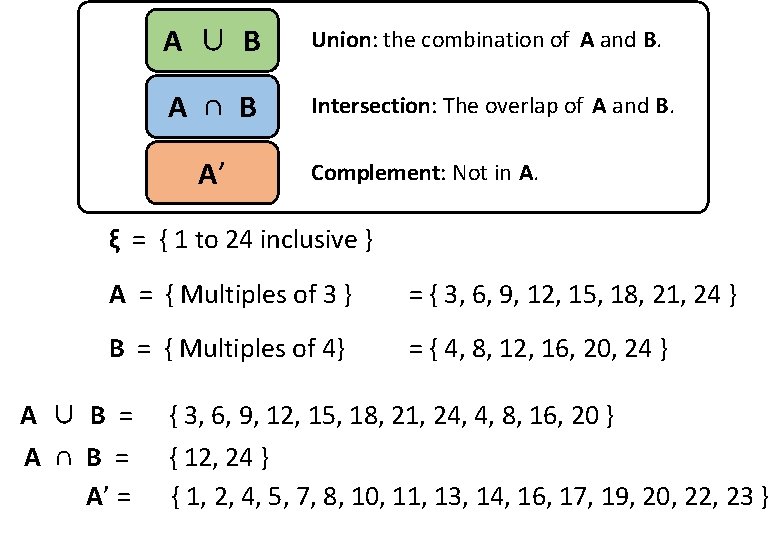
A ∪ B Union: the combination of A and B. A ∩ B Intersection: The overlap of A and B. A’ Complement: Not in A. ξ = { 1 to 24 inclusive } A = { Multiples of 3 } = { 3, 6, 9, 12, 15, 18, 21, 24 } B = { Multiples of 4} = { 4, 8, 12, 16, 20, 24 } A ∪ B = A ∩ B = A’ = { 3, 6, 9, 12, 15, 18, 21, 24, 4, 8, 16, 20 } { 12, 24 } { 1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23 }

ξ = { The alphabet } A = { O, R, A, N, G, E } B = { Vowels } A ∪ B = { O, R, A, N, G, E, I, U } A ∩ B = { O, A, E } ξ = { 1 to 20 inclusive } A = { Factors of 12 } B = { Multiples of 3 } A ∪ B = { 1, 2, 3, 4, 6, 12, 9, 15, 18 } ξ = { 10 to 30 inclusive } A = { Factors of 36 } B = { Multiples of 9 } A ∩ B = { 18 } ξ = { 3, 6, 7, 11, 12, 15, 17, 22, 25 } A = { Prime Numbers } B = { 3, 7, 12, 17, 25 } A ∩ B = { 3, 7, 17 } A’ = { 6, 12, 15, 22, 25 } ξ = { 1 to 30 inclusive } A = { Factors of 42 } B = { Multiples of 2 } (A ∪ B)’ = { 5, 9, 11, 13, 15, 17, 19, 23, 25, 27, 29 }

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk