Sets Set Operations 1 Basic discrete structures Discrete

Sets & Set Operations 1

Basic discrete structures • Discrete math: Study of the discrete structures used to represent discrete objects • Many discrete structures are built using sets • Sets : collection of objects • Examples of discrete structures built with the help of sets: • Combinations • Relations • Graphs 2

Set • Definition: A set is a (unordered) collection of objects. These objects are sometimes called elements or members of the set. (Cantor's naive definition). • A naïve theory in the sense of "naïve set theory" is a nonformalized theory, that is, a theory that uses a natural language to describe sets and operations on sets. 3

• • • Examples: – Vowels in the English alphabet V = { a, e, i, o, u } – First seven prime numbers. X = { 2, 3, 5, 7, 11, 13, 17 } 4

Representing sets • Representing a set by: • 1) Listing (tabulation method)) the members of the set. • 2) Definition by property, using the set builder notation. (Rule method) {x| x has property P}. • Example: • Even integers between 50 and 63. • 1) E = {50, 52, 54, 56, 58, 60, 62} • 2) E = {x| 50 <= x < 63, x is an even integer} 5

• • • If enumeration of the members is hard we often use ellipses. Example: a set of integers between 1 and 100 A= {1, 2, 3 …, 100} Rational numbers Q = {p/q | p ∈ Z, q ≠ 0} 6

Set can be § Finite set § Infinite set § Singleton set 7

• A set is determined only when we know definitely what object it contains. There must be no ambiguity or doubt in this regard. • Example: The collection of all tall students in a college does not define a set. • Because there will always be some doubt about as to which boys are to be regarded as tall. • For this reason the objects of a set are required to be “well defined”. • Thus, if we speak of the collection of all students in a college who are above 170 cms then we are actually speaking of set. 8

Interval Notation 9

Universal Set and Empty Set • The universal set U is the set containing everything currently under consideration. • Content depends on the context. • Sometimes explicitly stated, sometimes implicit. • The empty set is the set with no elements. • Symbolized by ∅ or { } 10

Things to remember 11

Equal sets • Definition: Two sets are equal if and only if they have the same elements. Example: • {1, 2, 3} = {3, 1, 2} = {1, 2, 1, 3, 2} Note: Duplicates don't contribute anything new to a set, so remove them. The order of the elements in a set doesn't contribute anything new. 12

Subsets • Definition: A set A is said to be a subset of B if and only if every element of A is also an element of B. • We use A ⊆ B to indicate A is a subset of B. • Example: A={1, 2, 3}, B={1, 2, 3, 4, 5}, C={2, 3, 5, 6} Clearly A ⊆ B and A ⊄ C 13

Proper Subset • In the example A={1, 2, 3}, B={1, 2, 3, 4, 5} We observe that the set B which contains A as subset, contains elements that are not in A. In such a situation we say that the set A is Properly contained in B or is a Proper subset of B. A⊂B proper subset / strict subset 14

Things to remember • • • Every set is a subset of itself Two sets A and B are equal if and only if A ⊆ B and B ⊆ A. The Null set ∅ is a subset of every set A. For any sets A, B, and C if A ⊆ B and B ⊆ C then A ⊆ C. For any sets A, B, C if A=B AND B=C, then A=C. 15

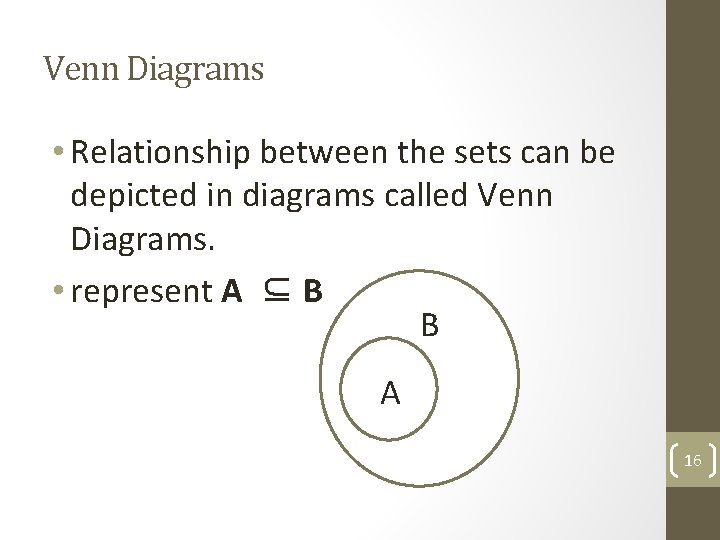
Venn Diagrams • Relationship between the sets can be depicted in diagrams called Venn Diagrams. • represent A ⊆ B B A 16

For any sets A, B, and C if A ⊆ B and B ⊆ C then A ⊆ C. • The truth of the above statement is obvious from the following Venn diagram. C B A 17

The Null set ∅ is a subset of every set S 18

Power Set • Given a set S, the power set of S is the set of all subsets of S. The power set is denoted by P(S). • Example: Consider set A={a, b} P(A)={∅, {a}, {b}, {a, b}= )={∅, {a}, {b}, A} If A={1, 2, 3} P(A)={∅, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, A} If a finite set A has n elements, then P(A) has 2 n elements. 19

If a finite set has n elements, prove that the power set of A has 2 n elements • If a finite set has n elements, then subset of A can have • No element(Null set) • One element(singleton set) • Two elements(each combination of two elements of A) • Three elements(each combination of three elements of A) • …… n-1 elements and n elements(A itself) n Binomial theorem: (1+x) • Null set( 1 in number) • Singleton sets: n in number: nc 1 • Each combination of two elements of A gives a subset of A containing two elements: nc 2 • Each combination of 3 elements of A gives a subset of A containing 3 elements : nc 3 • . . . ncn-1 • n elements… ncn 1+nc 2+nc 3……………+ncn-1+ncn= (1+1)n= 2 n 20

Cardinality 21 |{∅}| = 1

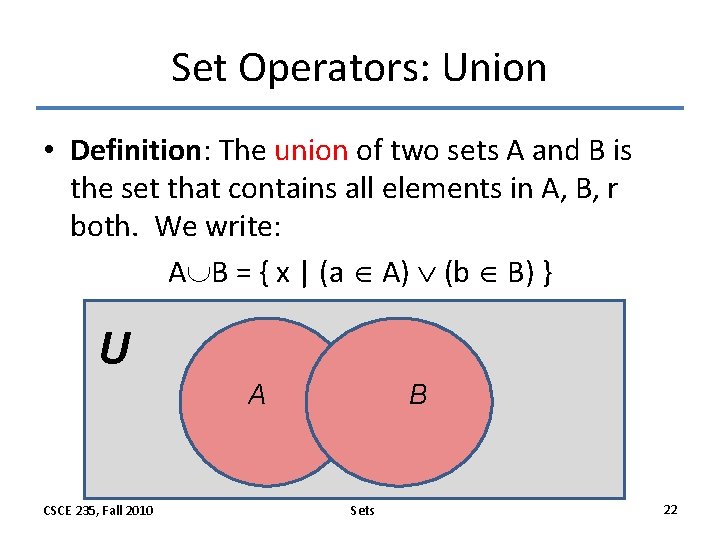
Set Operators: Union • Definition: The union of two sets A and B is the set that contains all elements in A, B, r both. We write: A B = { x | (a A) (b B) } U A CSCE 235, Fall 2010 B Sets 22

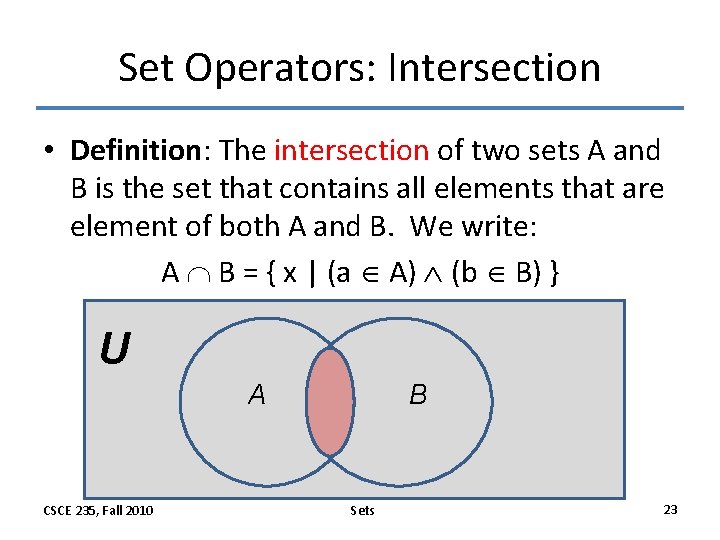
Set Operators: Intersection • Definition: The intersection of two sets A and B is the set that contains all elements that are element of both A and B. We write: A B = { x | (a A) (b B) } U A CSCE 235, Fall 2010 B Sets 23

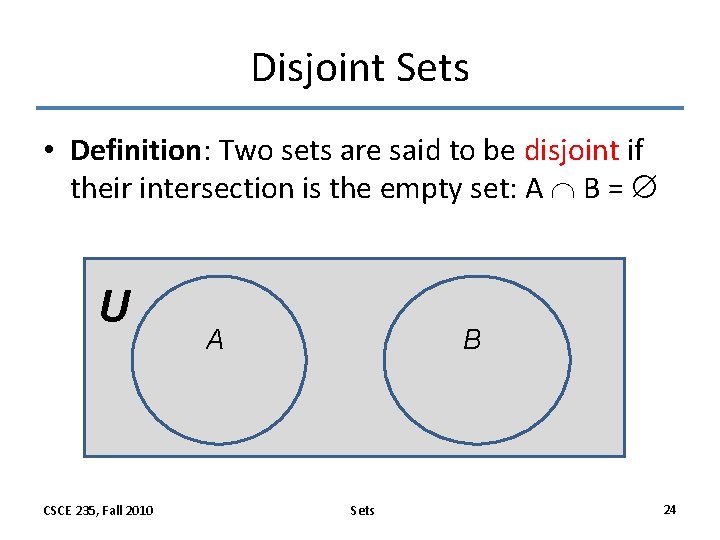
Disjoint Sets • Definition: Two sets are said to be disjoint if their intersection is the empty set: A B = U CSCE 235, Fall 2010 A B Sets 24

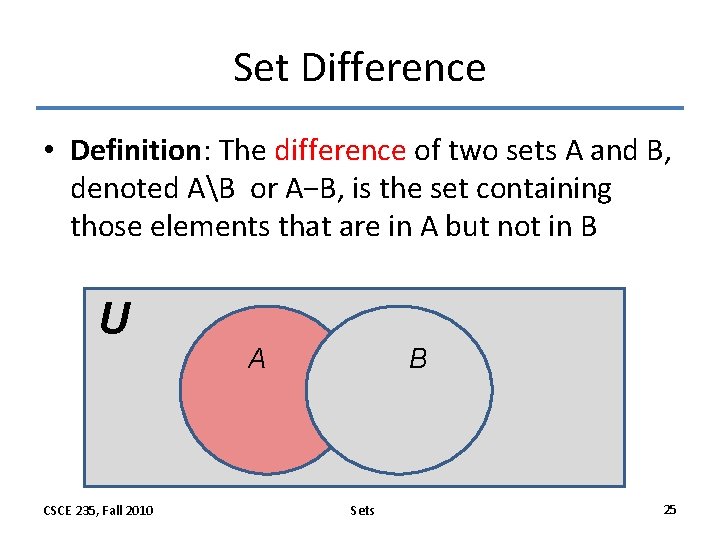
Set Difference • Definition: The difference of two sets A and B, denoted AB or A−B, is the set containing those elements that are in A but not in B U CSCE 235, Fall 2010 A B Sets 25

Set Complement • Definition: The complement of a set A, denoted A ($bar$), consists of all elements not in A. That is the difference of the universal set and A: UA A= AC = {x | x A } U CSCE 235, Fall 2010 A A Sets 26

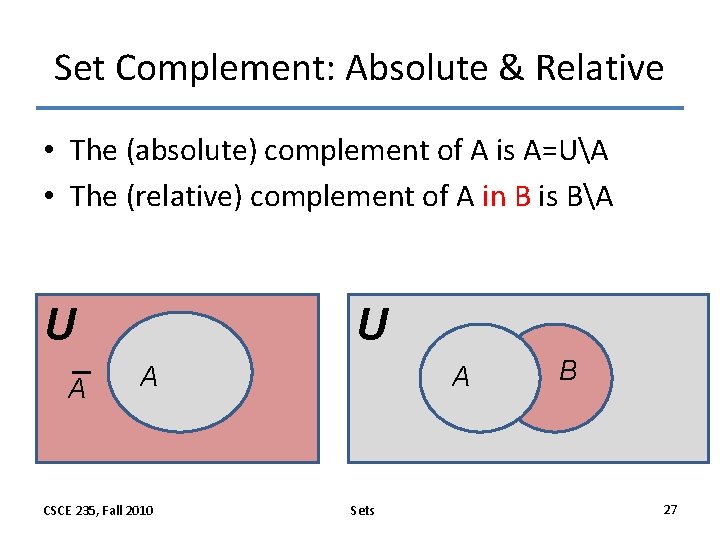
Set Complement: Absolute & Relative • The (absolute) complement of A is A=UA • The (relative) complement of A in B is BA U A CSCE 235, Fall 2010 A Sets B 27

Relative Compliment • Given two sets A and B, the set of all the elements that belong to B but not A is called the compliment of A relative to B(or relative compliment of A in B) and is denoted as B-A={x|x∈B and x ∉ A}. The set A-B(Relative compliment of B in A) can be defined similarly. B-A and A-B are not same CSCE 235, Fall 2010 Sets 28

Things to remember • • • For any sets A and B, the sets A-B and B-A are disjoint. If A and B are disjoint, then A-B=A, B-A=B. If U is a universal set and A ⊆ U, the U-A= Ac A=(A U B)-(B-A), B=(AUB)-(A-B) A=(A ∩ B)U(A-B), B=(A ∩ B)U(B-A) 29

Symmetric Difference • For Two sets A and B, the releative compliment of A ∩ B in A U B is called symmetric difference of A and B denoted as A∆B or A⊖B. • Simply A∆B= (A – B) ∪ (B – A) • A⊖B=(A U B)-(A ∩ B ) ={x|x ∈ A U B and x ∉ A ∩ B } 30

Set Identities Identity laws Domination laws Idempotent laws Complementation law A ∪ ∅= A A ∪U = U A ∪A = A A ∩U = A A ∩ ∅= ∅ A ∩A = A (A) = A Complement laws A ∩A = ∅ A ∪A = U 22 / 74

Set Identities (cont. ) Commutative laws A ∪B = B ∪A A ∩B = B ∩A Associative laws A ∪ (B ∪ C) = (A ∪ B) ∪ C A ∩ (B ∩ C) = (A ∩ B) ∩ C Distributive laws A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) Absorption laws A ∪ (A ∩ B) = A A ∩ (A ∪ B) = A De Morgan’s laws A ∪ B = A ∩B A ∩ B = A ∪B 23 / 74

Duality • • Each union replaced by intersection Each intersection replaced by union U by ∅ and ∅ by U If two sets P and Q are equal then their duals also equal. 33

Cartesian Product of sets • Definition: Let A and B be two sets. The Cartesian product of A and B, denoted Ax. B, is the set of all ordered pairs (a, b) where a A and b B Ax. B = { (a, b) | (a A) (b B) } • The Cartesian product is also known as the cross product 34

Cartesian Product • Cartesian Products can be generalized for any n-tuple • Definition: The Cartesian product of n sets, A 1, A 2, …, An, denoted A 1 A 2 … An, is A 1 A 2 … An ={ (a 1, a 2, …, an) | ai Ai for i=1, 2, …, n} CSCE 235, Fall 2010 Sets 35

36