SET THEORY Outline l l What is a

SET THEORY

Outline l l What is a set? Set Theory – Union – Intersection – etc l Sets in C – Pseudocode – Data Structures – Code

What is a set? l l l Set is an unordered collection of objects Written as: {9, 5, 3, 7, 1}, {red, blue, white} Can be – finite number of elements (no. students in this class) – infinite (number of real numbers) l l l Can contain any type of object Order of listing of set elements not important Duplicate elements do not appear

Examples l { 5, 6, 2, 1, 9, 8 } okay? – YES – unordered set of elements l { 1, 2, 3, 5, 8, 9 } okay? – YES – set of elements (order not important) l { 3, 7, 7, 9, 1, 5 } okay? – NO (Almost!) – wouldn’t contain duplicate elements, e. g. two ‘ 7’s

John Venn (1857 – 1923)

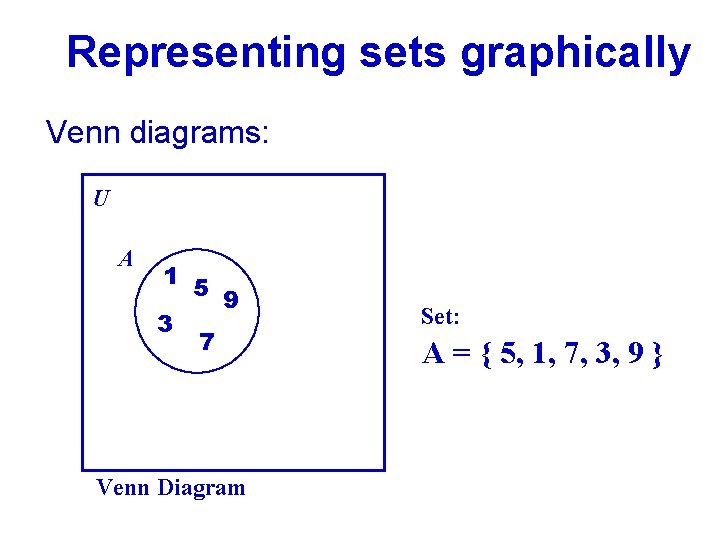
Representing sets graphically Venn diagrams: U A 1 3 5 9 7 Venn Diagram Set: A = { 5, 1, 7, 3, 9 }

Set terminology l Empty set (no elements): Æ – e. g. Set A = { }, A = Æ l If an object x is in a set A, write x Î A – e. g. Set A = { 1, 3, 5, 7, 9 } x=7 Then x Î A (Read: “x is in the set A”) l If not, write x A

Examples Set B = { 4, 9, 1, 2, 7, 6 } X=8 Y=9 XÎB? YÎB?

Universal sets l l Can define a universal set for particular area Universal set contains all possible elements under consideration E. g. could define U = set of all positive ints less than 10: U = {1, 2, 3, 4, 5, 6, 7, 8, 9} U A 1 59 37 Venn Diagram Universal set

Cardinality l Number of elements a set contains A = { 1, 2, 5, 6 } Cardinality of A = 4 B = { 2, 17 } Cardinality of B = 2

Set operations

Set intersection Intersection of sets A and B, written A B, is a new set containing only members common to A and B A = {1, 3, 5, 7, 9} B = {1, 2, 3, 4, 5} A B = ? {1, 3, 5}

Example A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 } B = { 21, 22, 10, 34, 12 } A B = ? { 10 }

Set operations : Union of two sets A and B, written A B, is a new set containing all members of A and B A = {1, 3, 5, 7, 9} A B = {1, 2, 3, 4, 5} ? {1, 2, 3, 4, 5, 7, 9} Note: Elements not duplicated in a union

Example A = { 1, 2, 3, 4 } B = { 2, 1, 3, 5 } C = { 3, 2, 1, 6 } A B C = ? { 1, 2, 3, 4, 5, 6 }

Set difference Difference of sets A and B, written A - B, is a new set containing members of A not in B A = {1, 3, 5, 7, 9} B = {1, 2, 3, 4, 5} A - B = ? {7, 9}

Set difference Difference of sets A and B, written A - B, is a new set containing members of A not in B A = {1, 3, 5, 7, 9} B = {1, 2, 3, 4, 5} B - A = ? {2, 4}

Subsets Set A is a subset of another set B, if all elements of A are contained within B. E. g. B = {1, 2, 3, 4, 5, 6, 7, 8, 9} A = {1, 3, 5, 7} then, A is a subset of B. Notation: A B

Venn Diagrams revisited

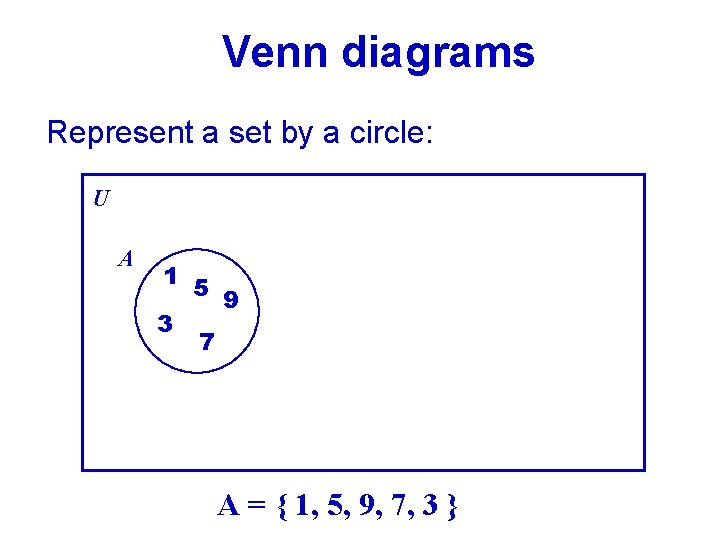
Venn diagrams Represent a set by a circle: U A 1 5 9 3 7 A = { 1, 5, 9, 7, 3 }

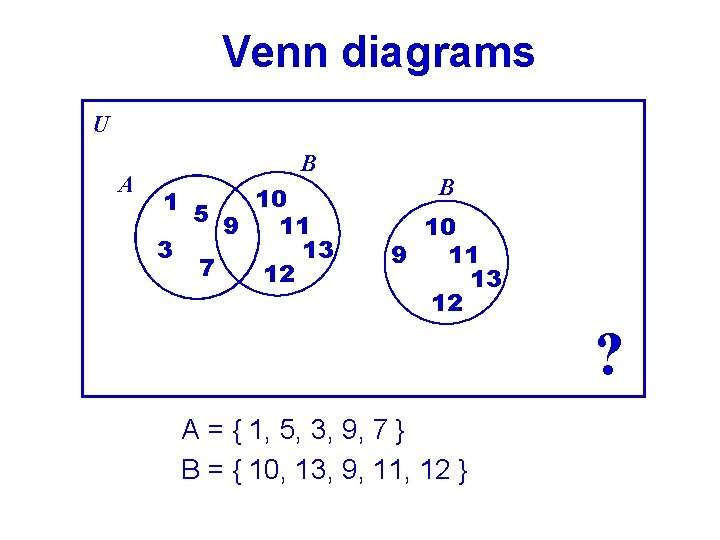
Venn diagrams U A B 10 1 5 11 9 3 13 7 12 B 10 9 11 13 12 ? A = { 1, 5, 3, 9, 7 } B = { 10, 13, 9, 11, 12 }

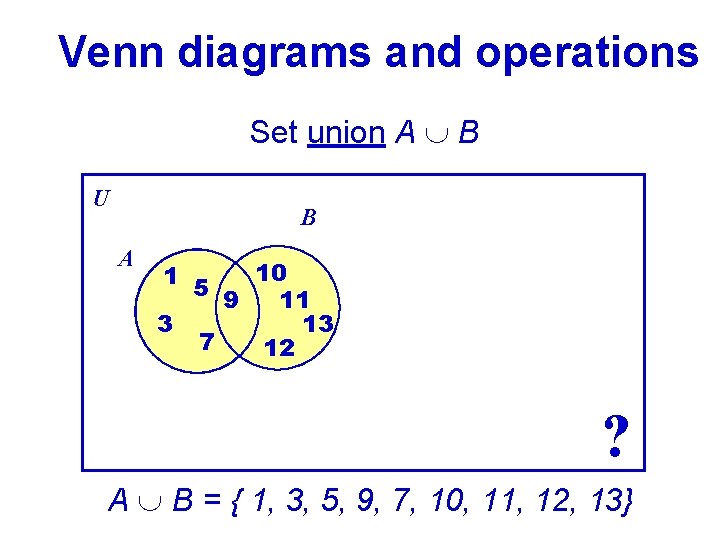
Venn diagrams and operations Set union A B U B A 10 1 5 9 11 3 13 7 12 ? A B = { 1, 3, 5, 9, 7, 10, 11, 12, 13}

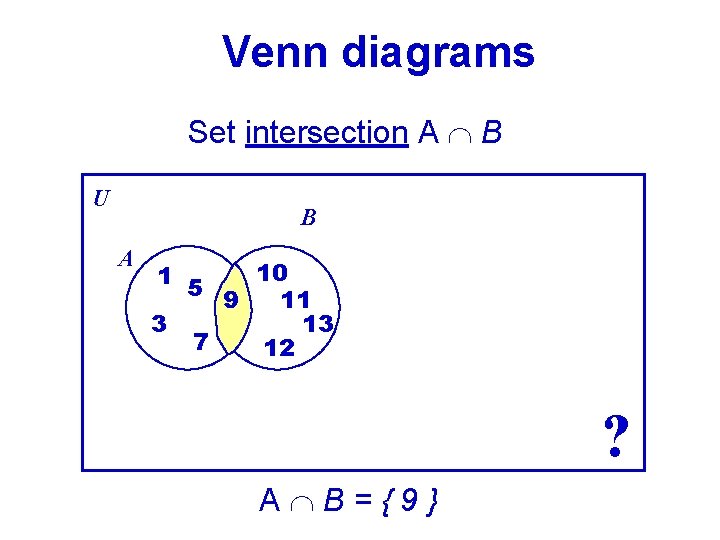
Venn diagrams Set intersection A B U B A 10 1 5 9 11 3 13 7 12 ? A B={9}

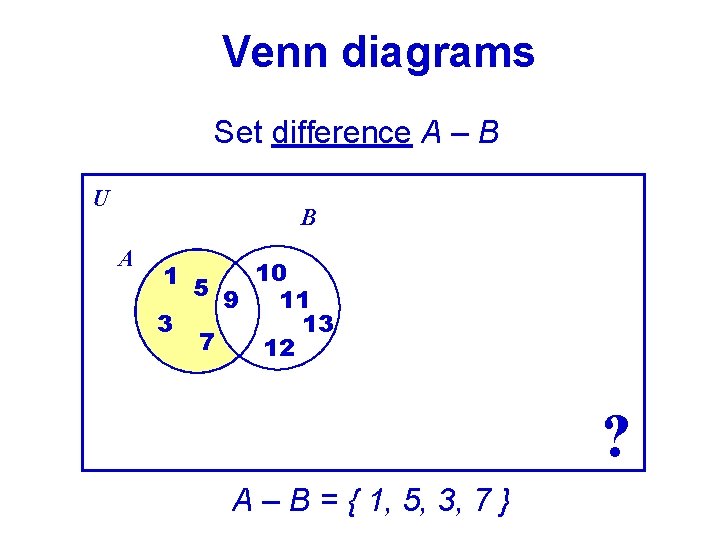
Venn diagrams Set difference A – B U B A 10 1 5 9 11 3 13 7 12 ? A – B = { 1, 5, 3, 7 }

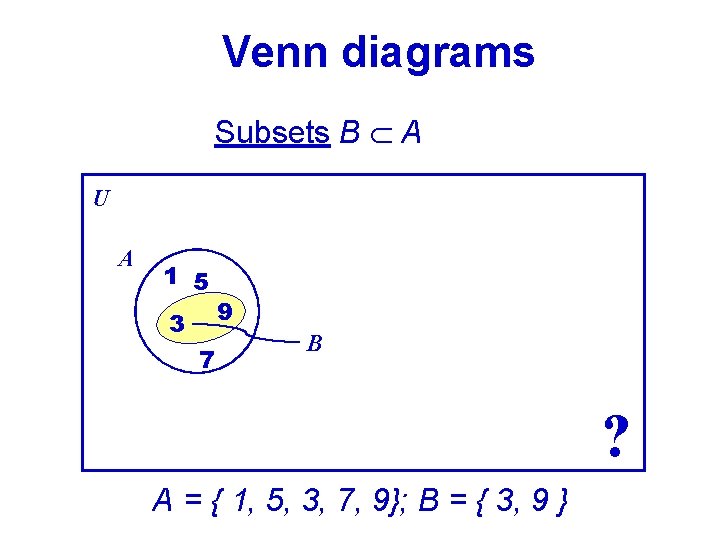
Venn diagrams Subsets B A U A 1 5 3 7 9 B ? A = { 1, 5, 3, 7, 9}; B = { 3, 9 }

l How would we represent sets using ‘c’ using linked lists?

Summary l Sets – Unordered collection of objects • No duplicates – Terminology • Empty set Æ • x Î A (“x is in the set A”) – Cardinality • Number of elements in a set – Operations • Union , intersection , difference -, subset – Representation : Venn Diagrams