SET IDENTITIES Lecture 09 SETS IDENTITIES Let A

SET IDENTITIES Lecture # 09

SETS IDENTITIES Let A, B, C be subsets of a universal set U. Idempotent Laws a. A A = A b. A A=A Commutative Laws a. A B = B A b. A B=B A Associative Laws a. A (B C) = (A B) C b. A (B C) = (A B) C

Distributive Laws a. A (B C) = (A B) (A C) b. A (B C) = (A B) (A C) Identity Laws a. A =A c. A U=U b. A = d. A U = A Complement Laws a. A Ac = U c. Uc = b. A Ac = d. c = U

Double Complement Law (Ac) c = A De-Morgan’s Laws a. (A B)c = Ac Bc b. (A B)c = Ac Bc Alternative Representation for Set Difference A – B = A Bc

Subset Laws a. A B C iff A C and B C b. C A B iff C A and C B Absorption Laws a. A (A B) = A b. A (A B) = A

EXERCISE Let A, B & C be subsets of a universal set U. Show that: A A B 2. A – B A 3. If A B and B C then A C 4. A B if, and only if, Bc Ac 1.

SOLUTION 2. A–B A Solution: Let x A – B x A and x B x A (by definition of A – B) (in particular) But x is an arbitrary element of A – B A–B A (proved)

SOLUTION 3. If A B and B C, then A C Solution: Suppose that A B and B C Consider x A x B (as A B) x C (as B C) But x is an arbitrary element of A A C (proved)

SOLUTION 4. Prove that A B iff Bc Ac Solution: Suppose A B Let x Bc x B x Ac {To prove Bc Ac} (by definition of Bc) (A B if x A then x B contrapositive: if x B then x A) (by definition of Ac) Thus if we show for any two sets A and B, if x B then x A. But x is an arbitrary element of Bc Ac

CONT… Conversely, Suppose Bc Ac {To prove A B} Let x Ac x Bc x B (by definition of Ac) ( Bc Ac) (by definition of Bc) But x is an arbitrary element of A. A B (proved)

SOLUTION 1. A A B Solution: Let x be the arbitrary element of A, that x A or x B x A B But x is an arbitrary element of A. A A B (proved)

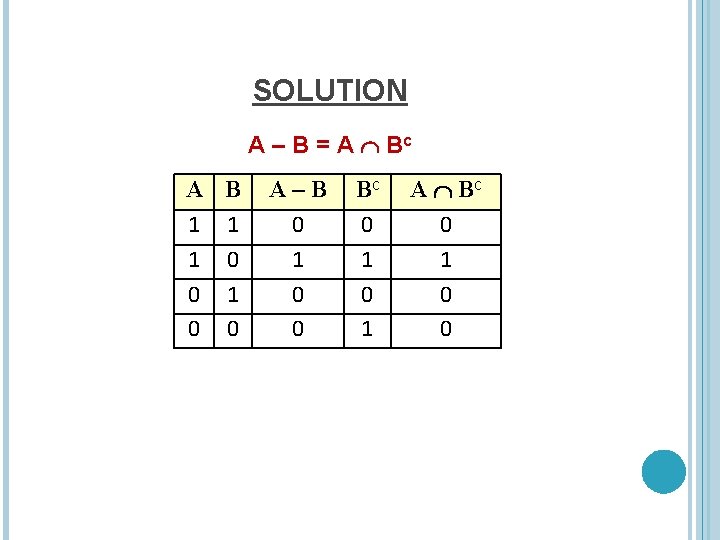
EXERCISE Let A, B & C be subsets of a universal set U. Prove that: A – B = A Bc EQUAL SETS: Two sets are equal if first is subset of second and second is subset of first. A – B A Bc and A Bc A – B

SOLUTION Let x A – B A and x B (definition of set difference) x A and x Bc (definition of complement) x A Bc (definition of intersection) x But x is an arbitrary element of A – B So we can write: A – B A Bc…………. (1)

CONT… Conversely, Let y A Bc y A and y Bc (definition of intersection) y A and y B (definition of complement) y A–B (definition of set difference) But y is an arbitrary element of A Bc A – B…………. (2) From (1) and (2) it follows that A – B = A Bc (as required)

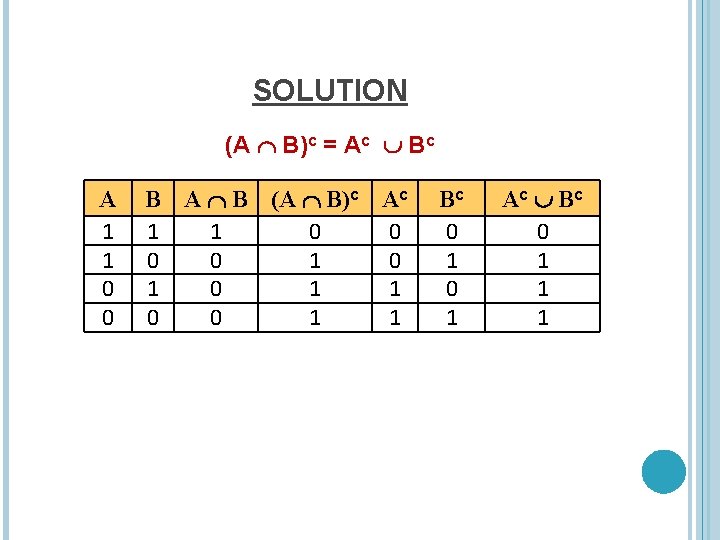
DEMORGAN’S LAW (A B)c = Ac Bc EQUAL SETS: Two sets are equal if first is subset of second and second is subset of first. (A B)c Ac Bc and Ac Bc (A B)c

PROOF First we show that (A B)c Ac Bc Let x (A B) c x A B (definition of complement) x A and x B (De. Morgan’s Law of Logic) x Ac and x Bc (definition of complement) x Ac Bc (definition of intersection) But x is an arbitrary element of (A B)c so we have proved that: (A B) c Ac Bc………(1)

CONT… Conversely, Let y Ac Bc y Ac and y Bc y A and y B y A B y (A B) c (definition of intersection) (definition of complement) (definition of set difference) (definition of complement) But y is an arbitrary element of Ac Bc A B…………. (2) From (1) and (2) it follows that (A B) c = Ac Bc (Demorgans Law)

ASSOCIATIVE LAW A (B C) = (A B) C PROOF: First we show that A (B C) (A B) C Consider x A (B C) x A and x B C (definition of intersection) x A and x B and x C (definition of intersection) x A B and x C (definition of intersection) x (A B) C (definition of intersection) But x is an arbitrary element of A (B C) (A B) C……(1)

CONT… Conversely, Let y (A B) C y A B and y C (definition of intersection) y A and y B and y C (definition of intersection) y A and y B C (definition of intersection) y A (B C) (definition of intersection) But y is an arbitrary element of (A B) C A (B C)……. . (2) From (1) & (2), we conclude that A (B C) = (A B) C (proved)

USING SET IDENTITIES For all subsets A and B of a universal set U, prove that (A – B) (A B) = A PROOF: LHS: = (A – B) (A B) = (A Bc) (A B) (Alternative representation for set difference) = A (Bc B) Distributive Law =A U Complement Law =A Identity Law = RHS (proved)

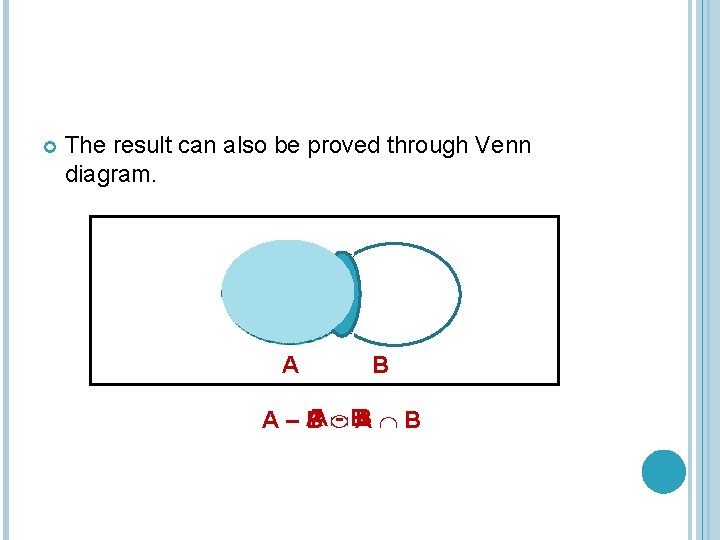
The result can also be proved through Venn diagram. A B A -B B A–A B

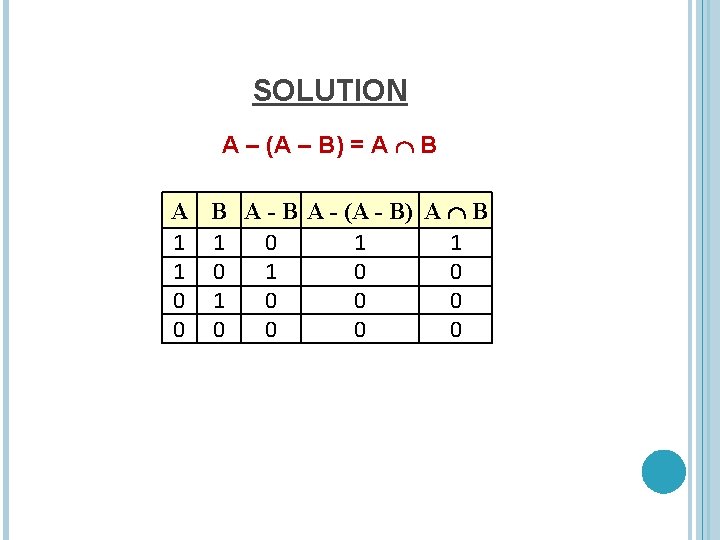
EXERCISE A – (A – B) = A B PROOF: LHS = A – (A – B) = A – (A Bc) Alternative representation for set difference = A (A Bc)c Alternative representation for set difference = A ((Ac (Bc)c) De. Morgan’s Law = A (Ac B) Double Complement Law = (A Ac) (A B) Distributive Law = (A B) Complement Law =A B Identity Law = RHS (proved)

EXERCISE (A – B) – C = (A – C) – B PROOF: LHS = (A – B) – C = (A Bc) – C Alternative representation for set difference = (A Bc) Cc Alternative representation for set difference = A (Bc Cc) Associative Law = A (Cc Bc) Commutative Law = (A Cc) Bc Associative Law = (A – C) Bc Alternative representation of set difference = (A – C) – B Alternative representation of set difference = RHS (proved)

EXERCISE Simplify Solution: (Bc – A))c = (Bc Ac))c Alternative representation for set difference = (Bc)c (Bc Ac)c De. Morgan’s Law = B (Bc Ac)c Double Complement Law = B ((Bc)c (Ac)c) De. Morgan’s Law = B (B A) Double Complement Law =B Absorption Law

PROVING SET IDENTITIES BY MEMBERSHIP TABLE Prove the following using Membership Table: 1. A – (A – B) = A B 2. (A B)c = Ac Bc 3. A – B = A Bc

SOLUTION A – (A – B) = A B A - (A - B) A B 1 1 0 1 0 0 0 0

SOLUTION (A B)c = Ac Bc A 1 1 0 0 B A B (A B)c Ac 1 1 0 0 1 0 1 1 0 0 1 1 Bc 0 1 Ac B c 0 1 1 1

SOLUTION A – B = A Bc A B 1 1 1 0 0 A–B 0 1 0 0 Bc 0 1 A Bc 0 1 0 0