SET 2 NETWORKS Network inference from repeated observations

SET 2 NETWORKS: Network inference from repeated observations of node sets Tanima Chatterjee CS 502

Overview Network inference – Uncovering the relation between entities through indirect evidence. • A general class of network inference problem. • Network inference approach. • Application: I. Inference of physical interactions: PPI II. Mount Sinai collaboration network.

Inference Approach ( using repeated sets ) • Vertices are entities and edges are relations. • Subsets of related molecular components are observed. Underlying network is not known. • Popular method of gene set enrichment analysis(GSEA) uses libraries of related gene sets stored in a Gene transposed matrix(GMT) format. • Each subset of related genes provides coarse info about underlying network structure.

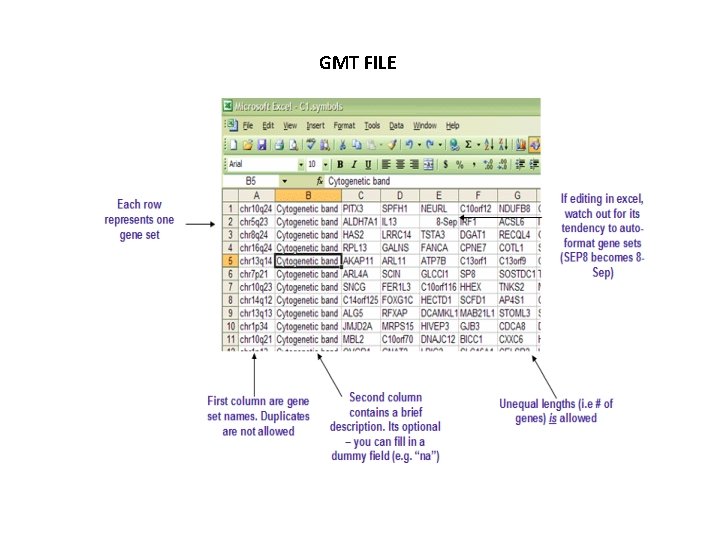
GMT FILE

The Inference P roblem • Input: a set of entities (genes or proteins or. . . ) in the form of a GMT file the results of experiments, or sampling more generally. • Assumptions: 1. An underlying network exists which relates the interactions between the entities in the GMT file 2. Each line of the GMT file contains information on the connectivity of the underlying network • The problem: Given a GMT file can we extract enough information to resolve the underlying network?

Exponential random graphs model • Used to generate an ensemble of network with statistical properties. • Set of graphs G represents a sample space in the model and , {xi}, i=1, 2…r , represent the set of r empirical values observed. • Probability distribution is P(G) defined over elements g of G, such that expected value of xi takes the empirical values. The following are the mathematical equations involved:

Dependence Graphs • ERGM can be generated in terms of dependence graphs • Dependence graphs can be represented in terms of adjacency matrix gi, j which is symmetric and has elements: gi, j = 1 , if vi and vj are connected by a vertex in G = 0 otherwise • The edges of Dependence graph D identifies pairs of edges whose presence in the model network depends on each other.

Approach • Given unknown underlying network Gu with vertices V. Set C ={ci , ci∈ V}, i = 1, . . , Nc. • Sets ci consist of vertices that are empirically observed to be related in the network. • The network inference problem is thus: Given the set of Nc subsets c, and no other information, to what extent can the underlying network Gu be inferred ?

• Observable graph functions, xi(G) can be defined as: xi(G)= 1 if the elements of ci form a connected subgraph of G = 0 otherwise. • If we have a confidence α that the elements in each line are locally connected, the constraints on the ensemble are: ∑G P(G)xi(G)=α • G is the sample set that consists of simple undirected graphs. • C is the accumulation of coarse information on the connectivity of the underlying network.

Algorithm for generating G For i = 1 to Ng Randomly permute the order of lines in the GMT file Ei ={} (Start with a graph with no links) For j = 1 to NC Randomly introduce the minimal number of edges between the vertices ci such that they are connected and continually append to set Ei. End for j End for i Calculate the mean adjacency matrix of ensemble, Gens

Analytic Approximation • When applying this approach to real data typically there are large numbers of nodes • Sample space of networks can be very large -> computationally demanding • Write a simple analytical approximation which mimics the action of the algorithm. • The probability that a given edge is present in Gu :

Bias Adjustment: • GMT file data is randomly permuted, by conserving the lengths of each set and frequency of each element. • Allow only one of each type in a given set/line, calculate edge weights. • Process is repeated and null distributions for each edge weights are calculated. • Actual edge weight is compared to the null distribution, under the hypothesis of no interaction, p-value is obtained.

Matthews correlation coefficient • Evaluates quality of predicted edges MCC = (TP*TN – FP*FN) / √( (TP+ FP)(TP + FN)(TN + FP)TN + FN) FN and FP are false positives and negatives respectively TN and TP are true positives and negatives respectively

Accuracy of Inference • How similar is the inferred network to the underlying network ? • Quality of the inference depends on three parameters: 1. GMT file. 2. Length of lines in GMT file. 3. Number of nodes in the underlying network.

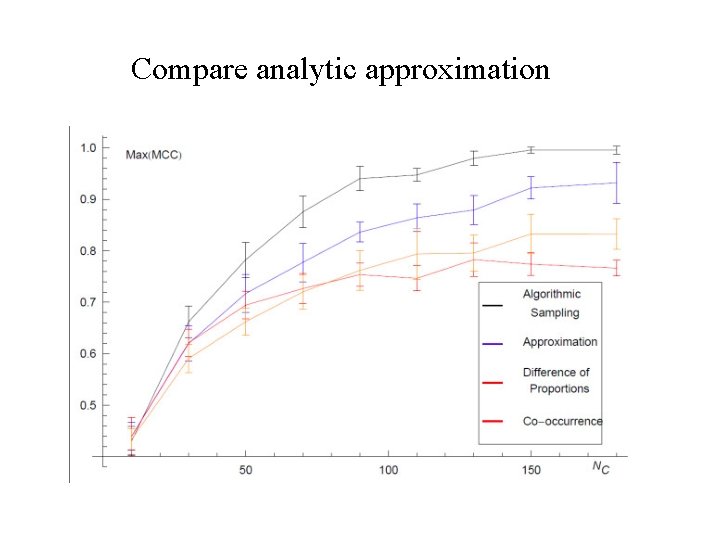
Compare analytic approximation

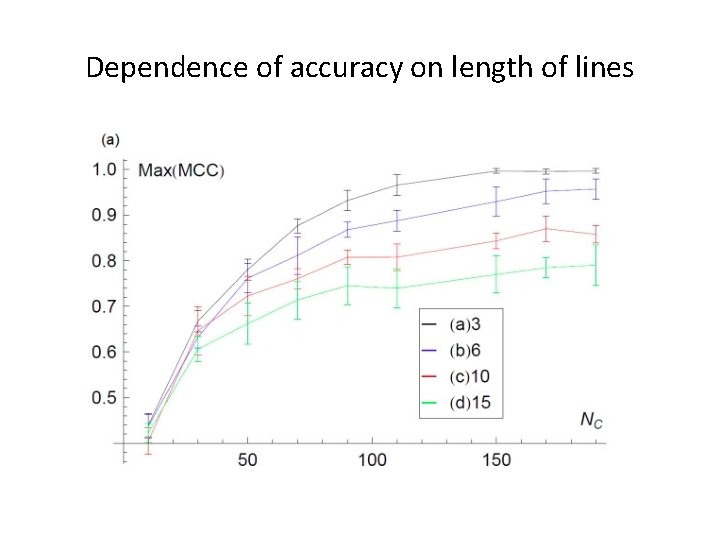
Dependence of accuracy on length of lines

Applications • The applications of the network inference from repeated observations of sets to systems biology which are discussed by the authors are: 1. inference of physical interactions: PPI 2. Inference of gene associations: Stem cell genes 3. inference of statistical interactions: Drug/side effect network • We discuss here in detail the first one of protein interactions

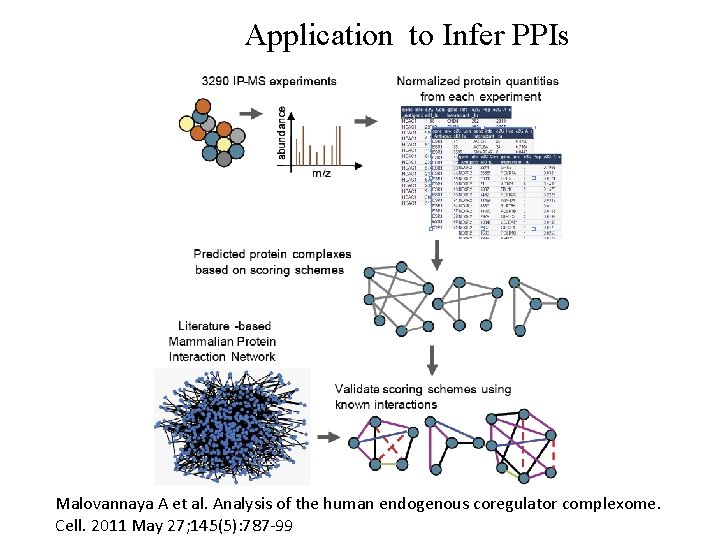
Application to Infer PPIs Malovannaya A et al. Analysis of the human endogenous coregulator complexome. Cell. 2011 May 27; 145(5): 787 -99

Validation of Inferred Network • Compare inferred PPI network to the following databases: Ø Bio. Carta Ø HPRD PPIInnate. DB Ø Int. Act Ø KEGG Ø MINT mammalia Ø MIPS Ø Bio. Grid

Mount Sanai Collaboration network • This is a broader application of the network inference approach. • The GMT representation lends naturally to the inference of co-authorship networks • Pub. Med E-utilities’ E-search function used to search the latest (early May 2012) publications that contain an affiliation equal to the term Mount Sinai School of Medicine. • Extracted the author list using the E fetch function. • For each paper, the data was formatted into a GMT file with the Pub. Med ID as the set label and each author of each paper as the members of each set.

Conclusion • In cases where direct determination of the network is difficult or impossible it is necessary to use indirect evidence which can be more easily obtained. • The authors have shown by providing statistical results that approximation is a better technique rather than using full algorithm when data set is huge and a GMT file. • Useful for addressing problems in current biology and biomedicine, the approach is of general significance and can be applied in other fields that study complex systems.

Future Work Three Future research questions on the following topic would be: • Relevance of network inference in Detecting congenital disorders. • Social network analysis using network inference on related sets. (FB and Twitter) • Use of informative network priors to streamline and sharpen the questions answered by network inference problem.

Thank you for your patience!!