Session 7 b Example Preventive Maintenance At the

Session 7 b

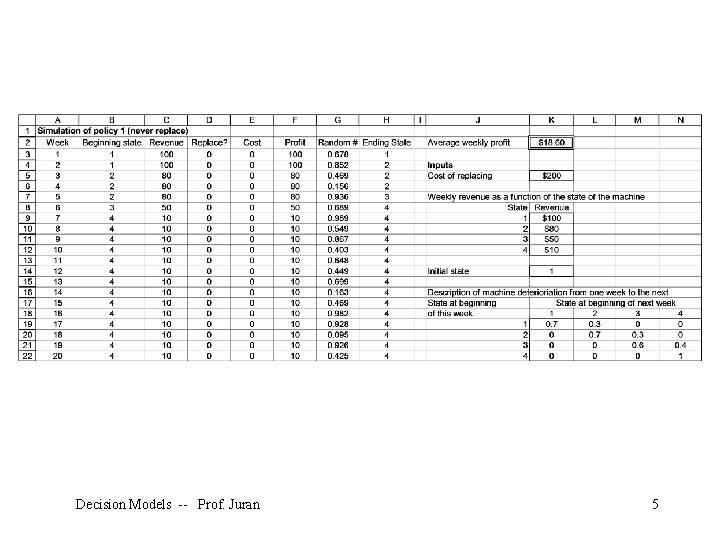
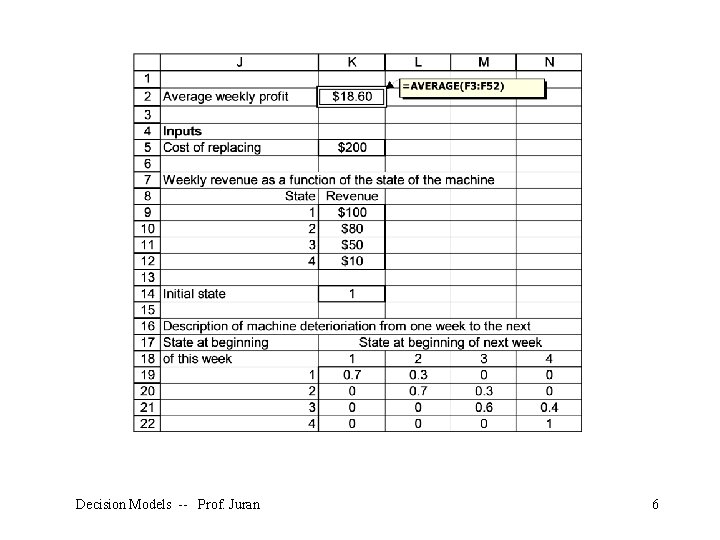
Example: Preventive Maintenance At the beginning of each week, a machine is in one of four conditions: 1 = excellent; 2 = good; 3 = average; 4 = bad. The weekly revenue earned by a machine in state 1, 2, 3, or 4 is $100, $90, $50, or $10, respectively. After observing the condition of the machine at the beginning of the week, the company has the option, for a cost of $200, of instantaneously replacing the machine with an excellent machine. Decision Models -- Prof. Juran 2

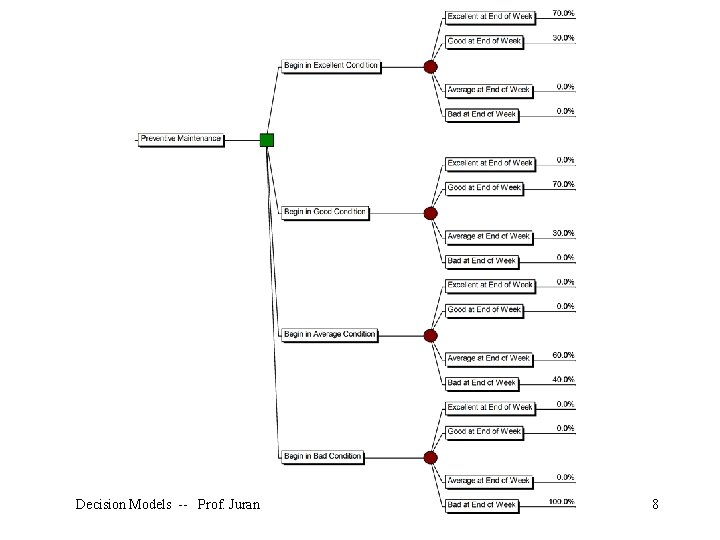
The quality of the machine deteriorates over time, as shown here. Decision Models -- Prof. Juran 3

Four maintenance policies are under consideration: § Policy 1: Never replace a machine. § Policy 2: Immediately replace a bad machine. § Policy 3: Immediately replace a bad or average machine. § Policy 4: Immediately replace a bad, average, or good machine Simulate each of these policies for 50 weeks (using 250 iterations each) to determine the policy that maximizes expected weekly profit. Assume that the machine at the beginning of week 1 is excellent. We’ll make use of the IF and RAND() functions Decision Models -- Prof. Juran 4

Decision Models -- Prof. Juran 5

Decision Models -- Prof. Juran 6

Decision Models -- Prof. Juran 7

Decision Models -- Prof. Juran 8

Boole argued that logic was principally a discipline of mathematics, rather than philosophy Developed a way to encode logical arguments into a language that could be manipulated and solved mathematically A binary system, with basic operations AND, OR and NOT, that is one of the principles of modern computing Decision Models -- Prof. Juran 9

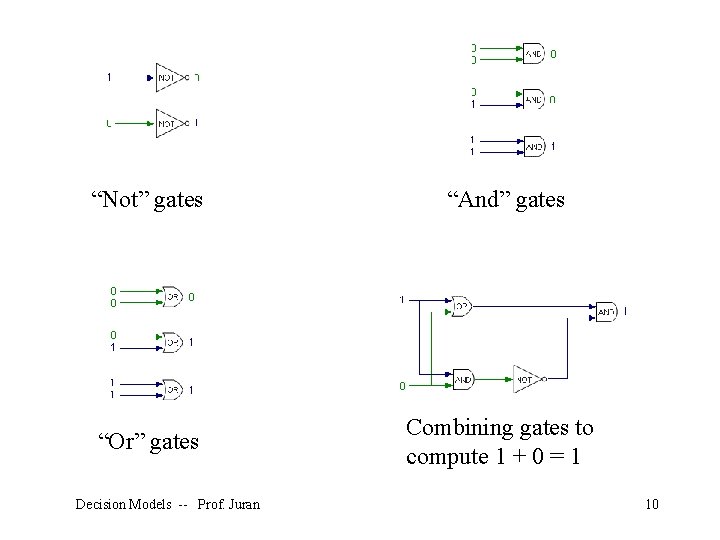
“Not” gates “And” gates “Or” gates Combining gates to compute 1 + 0 = 1 Decision Models -- Prof. Juran 10

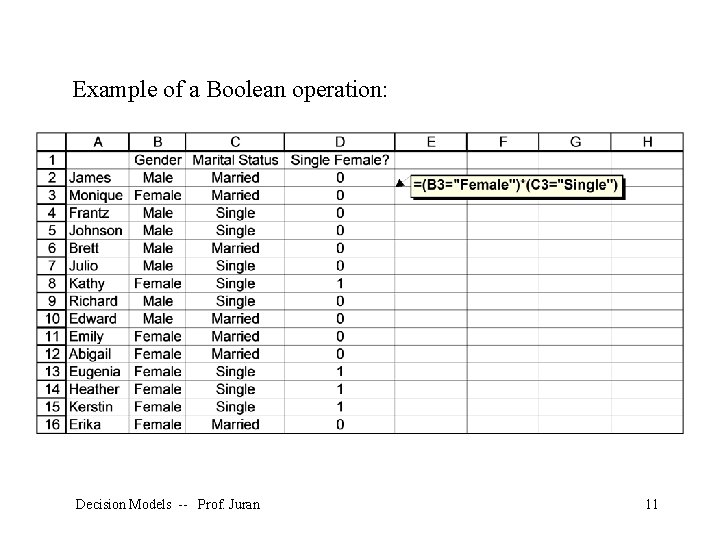
Example of a Boolean operation: Decision Models -- Prof. Juran 11

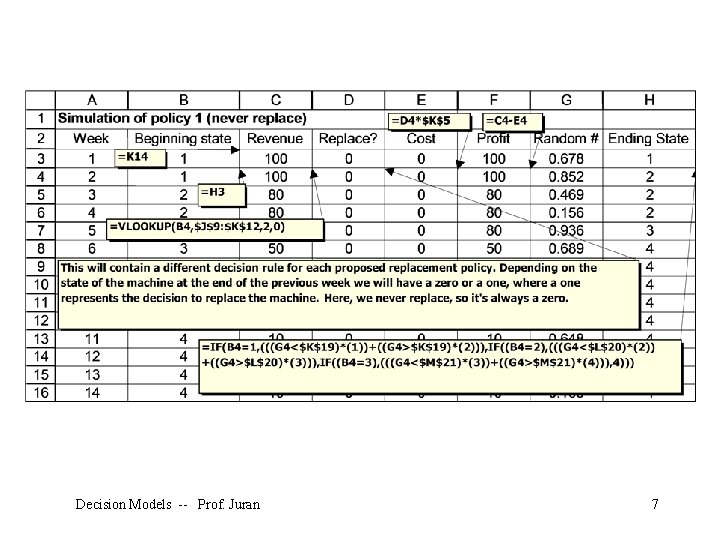
=((G 5<$K$19)*(1))+((G 5>$K$19)*(2)) In English, this translates as “ 1 if G 5 is less than K 19 and 2 if G 5 is not less than K 19”. We can have this cell return a 1 or a 2, based on the probability that G 5 is less than K 19. Our model uses statements like this, where G 5 is a uniform random variable between 0 and 1. Decision Models -- Prof. Juran 12

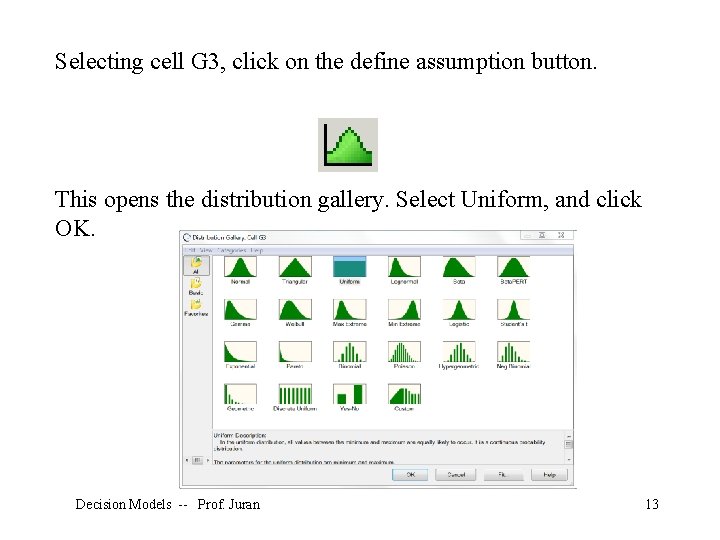
Selecting cell G 3, click on the define assumption button. This opens the distribution gallery. Select Uniform, and click OK. Decision Models -- Prof. Juran 13

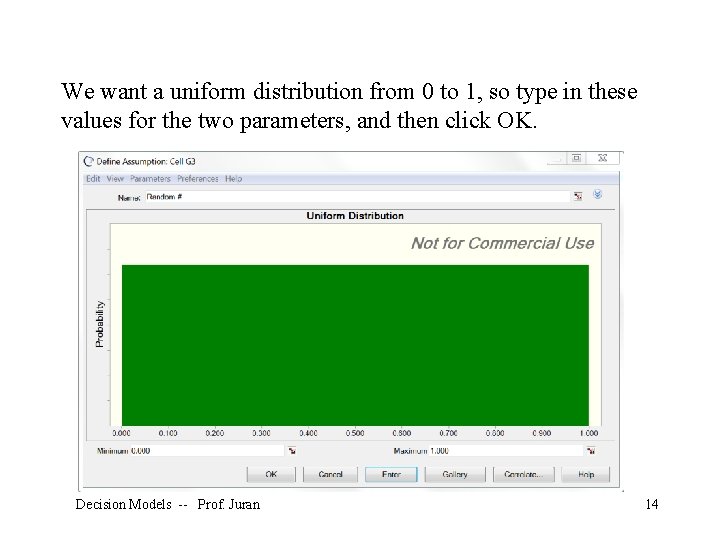
We want a uniform distribution from 0 to 1, so type in these values for the two parameters, and then click OK. Decision Models -- Prof. Juran 14

Decision Models -- Prof. Juran 15

We could use the same procedure to define all of the other assumption cells, but that would be tedious. Luckily, Crystal Ball has copy and paste buttons: Select the assumption cell you want to copy (G 3), and click the Crystal Ball copy button (not the regular Excel copy button). Then select the cells you want to define as assumptions (G 4: G 52), and click the Crystal Ball paste button. They will all turn green. Decision Models -- Prof. Juran 16

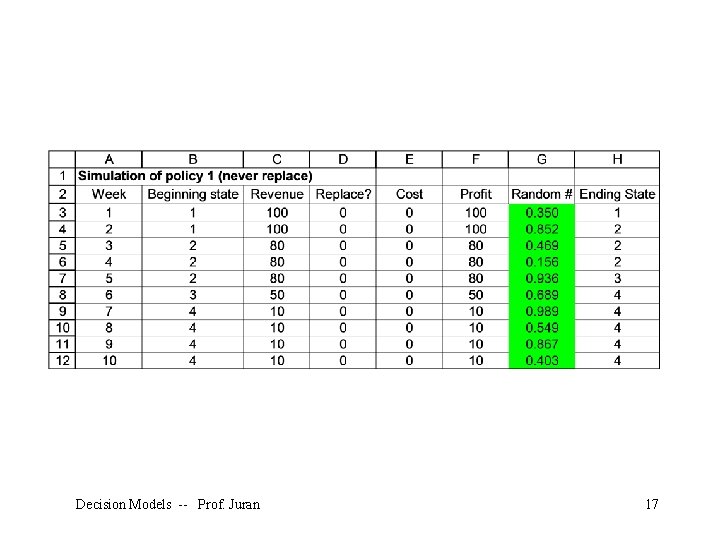
Decision Models -- Prof. Juran 17

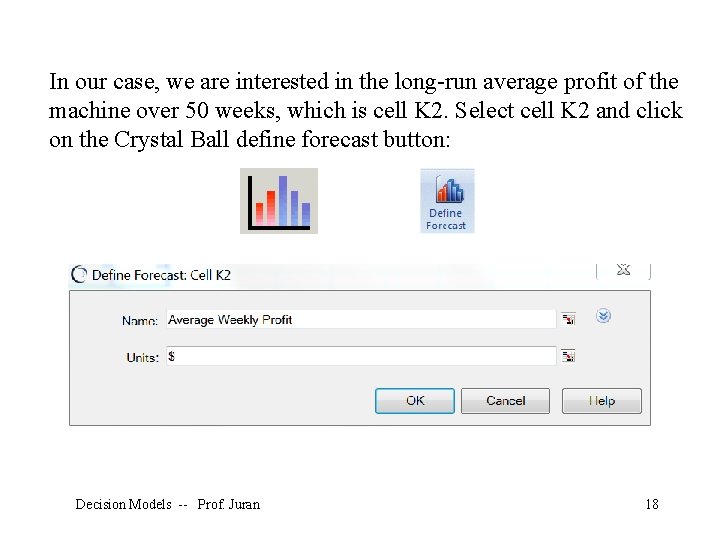
In our case, we are interested in the long-run average profit of the machine over 50 weeks, which is cell K 2. Select cell K 2 and click on the Crystal Ball define forecast button: Decision Models -- Prof. Juran 18

Decision Models -- Prof. Juran 19

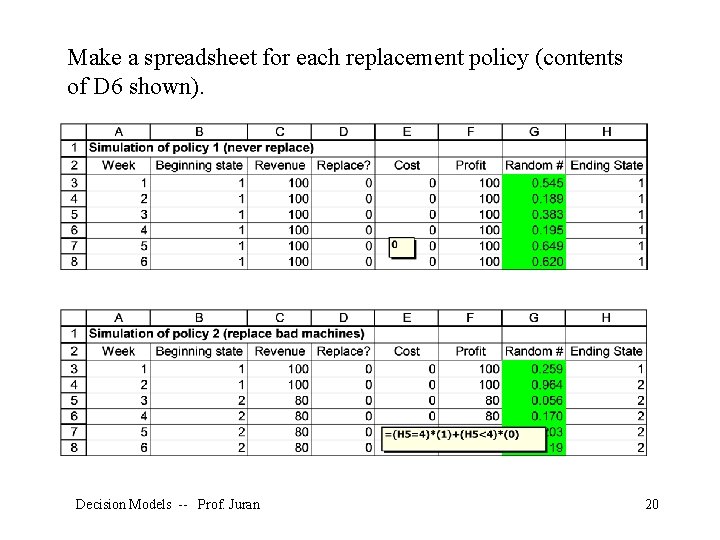
Make a spreadsheet for each replacement policy (contents of D 6 shown). Decision Models -- Prof. Juran 20

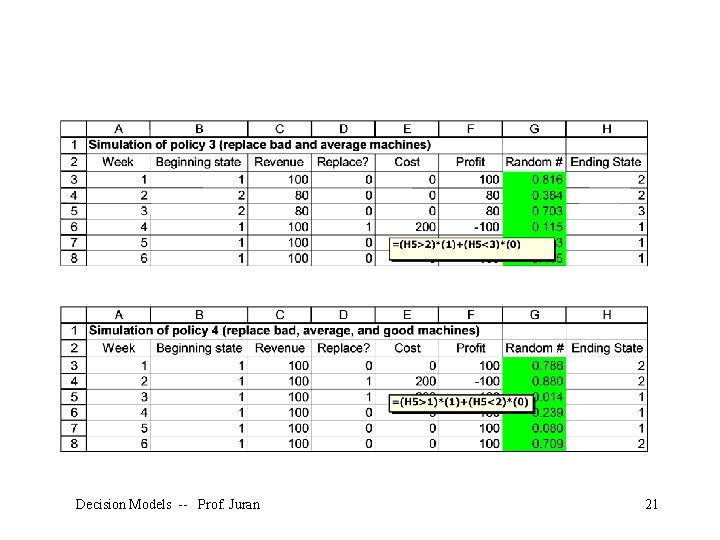
Decision Models -- Prof. Juran 21

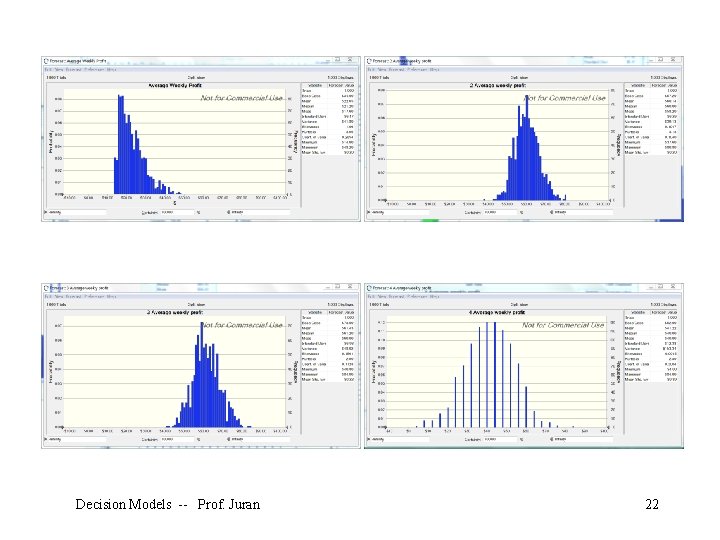
Decision Models -- Prof. Juran 22

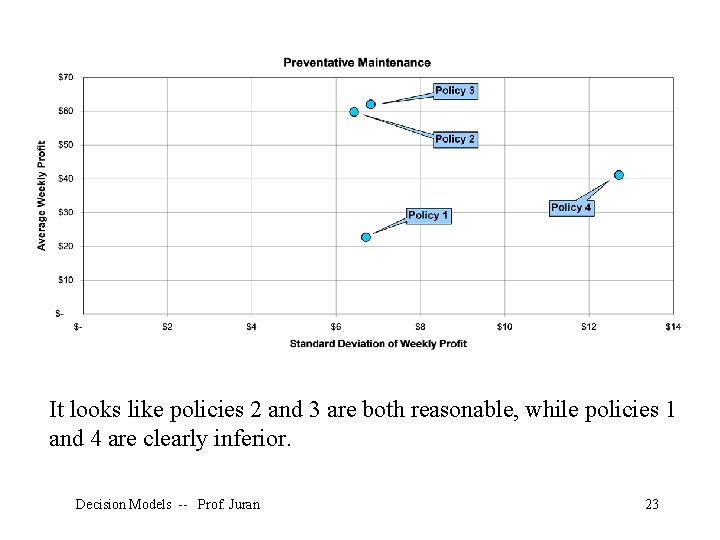
It looks like policies 2 and 3 are both reasonable, while policies 1 and 4 are clearly inferior. Decision Models -- Prof. Juran 23

Summary • Monte Carlo Simulation – Basic concepts and history • Excel Tricks – RAND(), IF, Boolean • Crystal Ball – Probability Distributions • Normal, Gamma, Uniform, Triangular – Assumption and Forecast cells – Run Preferences – Output Analysis • Examples – Coin Toss, TSB Account, Preventive Maintenance, NPV Decision Models -- Prof. Juran 24