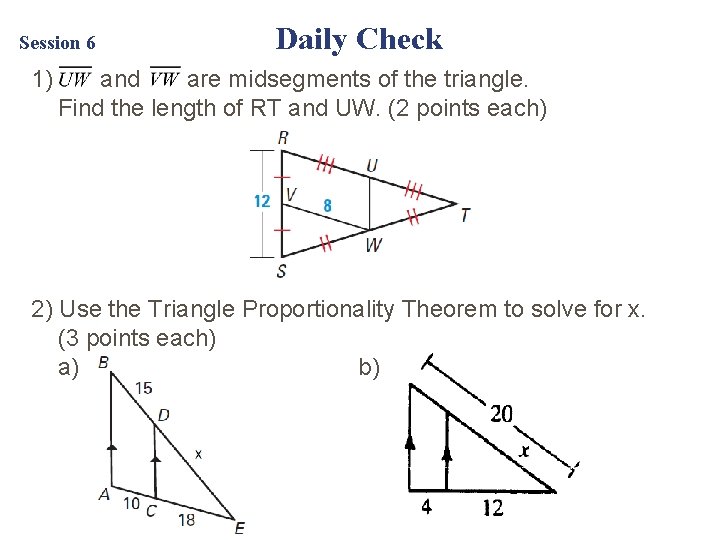
Session 6 1 Daily Check and are midsegments












- Slides: 33

Session 6 1) Daily Check and are midsegments of the triangle. Find the length of RT and UW. (2 points each) 2) Use the Triangle Proportionality Theorem to solve for x. (3 points each) a) b)

Homework Review Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

CCGPS Analytic Geometry Day 6 UNIT QUESTION: How do I prove geometric theorems involving lines, angles, triangles and parallelograms? Standards: MCC 9 -12. G. SRT. 1 -5, MCC 9 -12. A. CO. 6 -13 Today’s Question: What does it mean for two triangles to be congruent? Standard: MCC 9 -12. G. SRT 5, CO. 7 -8

Congruent triangles have congruent sides and congruent angles. The parts of congruent triangles that “match” are called corresponding parts. Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

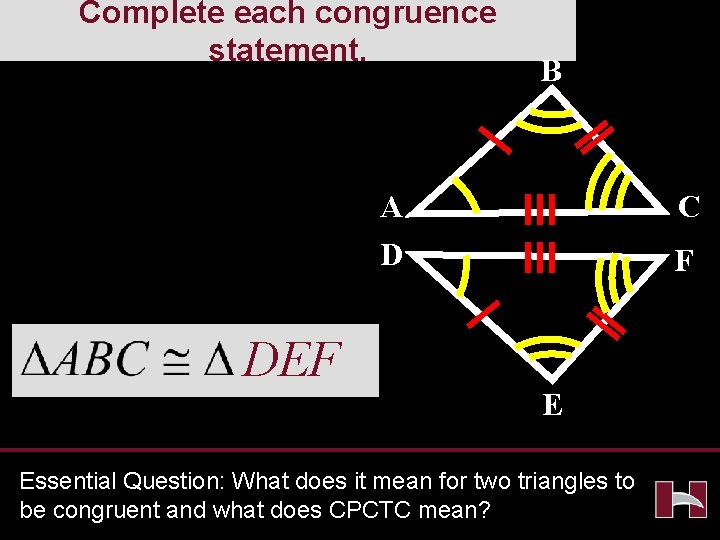
Complete each congruence statement. B A D DEF C F E Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

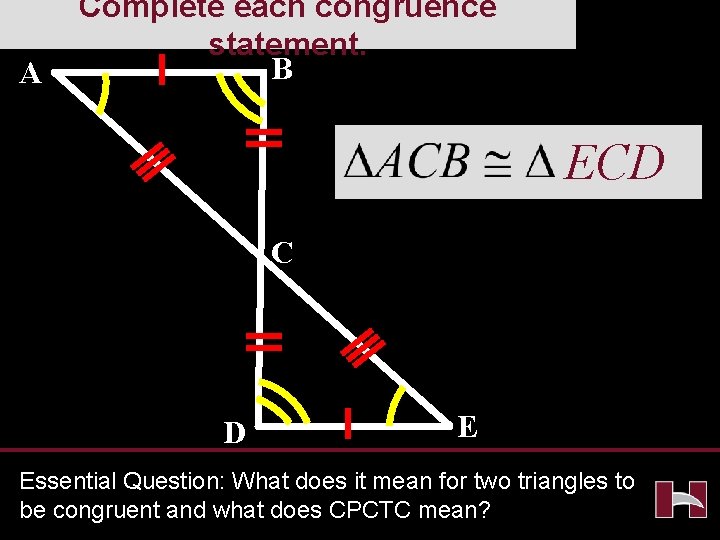
A Complete each congruence statement. B ECD C D E Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

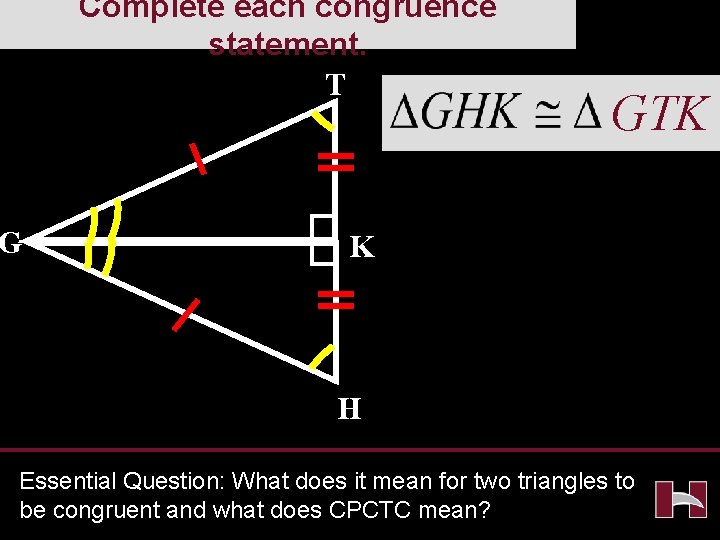
Complete each congruence statement. T G GTK K H Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

Corresponding Parts of Congruent Triangles are Congruent Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

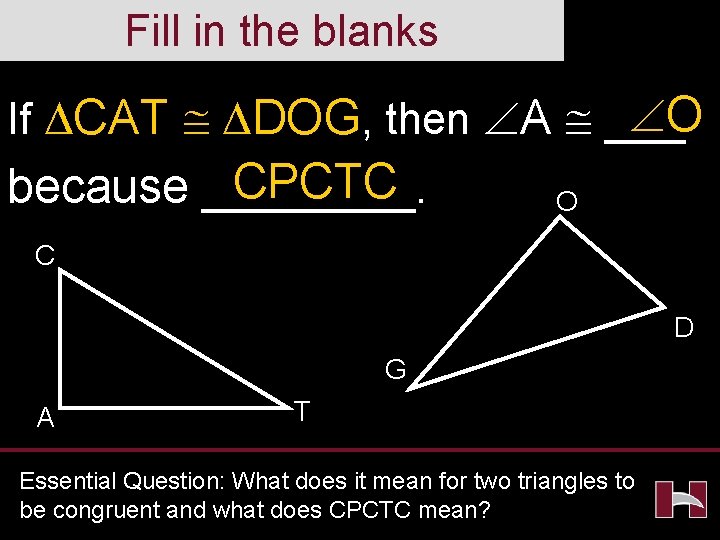
Fill in the blanks O If CAT DOG, then A ___ CPCTC because ____. O C D G A T Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

Fill in the blanks If FJH QRS, then ___ Q because _______. CPCTC and F ___ If XYZ ABC, then ___ CPCTC B because _______. and Y ___ Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

Essential Question: What does it mean for two triangles to be congruent and what does CPCTC mean?

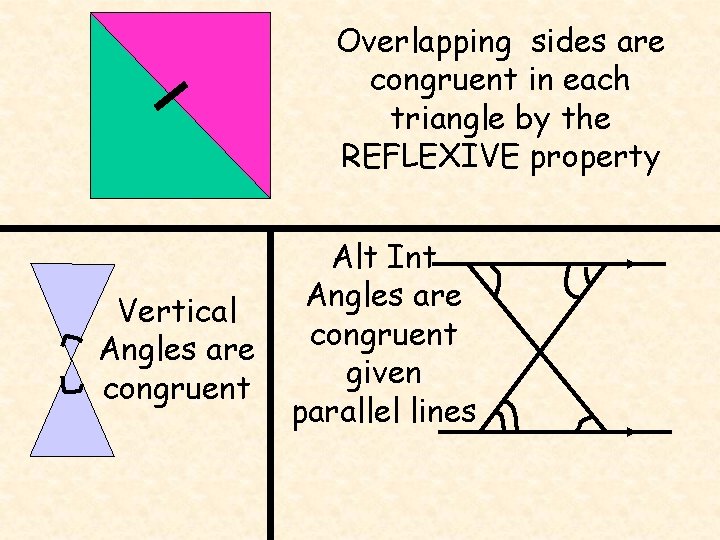
Overlapping sides are congruent in each triangle by the REFLEXIVE property Vertical Angles are congruent Alt Int Angles are congruent given parallel lines

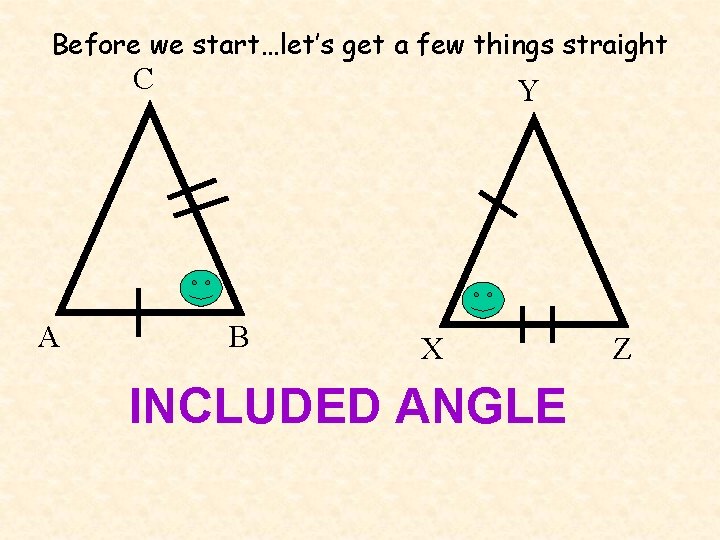
Before we start…let’s get a few things straight C A Y B X INCLUDED ANGLE Z

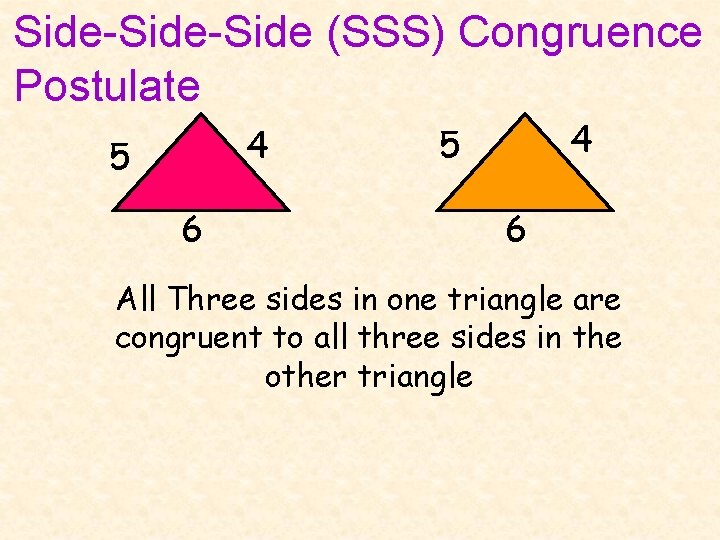
Side-Side (SSS) Congruence Postulate 4 5 6 All Three sides in one triangle are congruent to all three sides in the other triangle

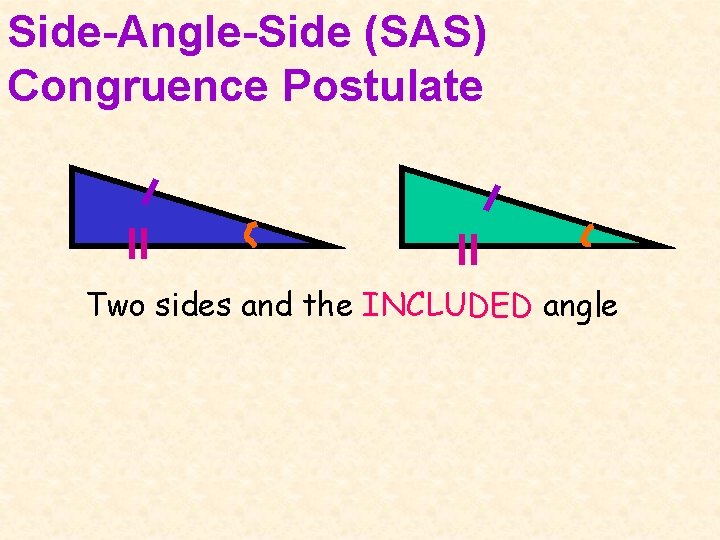
Side-Angle-Side (SAS) Congruence Postulate Two sides and the INCLUDED angle

Ex 1 DFE UVW SSS by ____

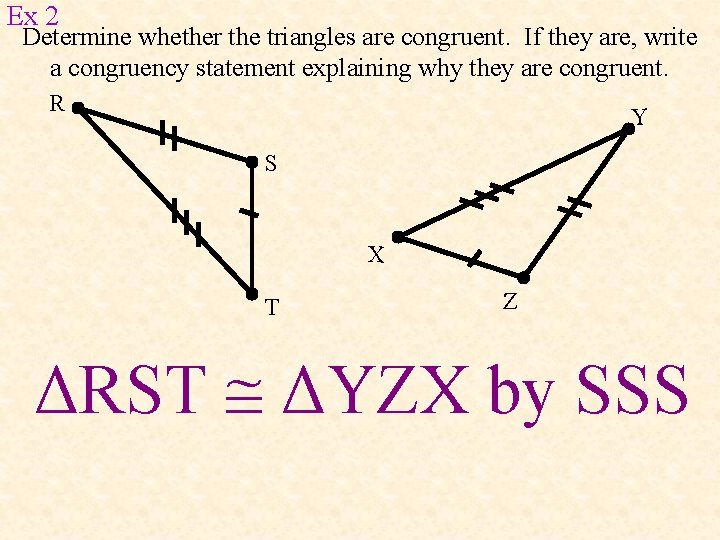
Ex 2 Determine whether the triangles are congruent. If they are, write a congruency statement explaining why they are congruent. R Y S X T Z ΔRST ΔYZX by SSS

Ex 3 Determine whether the triangles are congruent. If they are, write a congruency statement explaining why they are congruent. R B A T S Not congruent. Not enough Information to Tell C

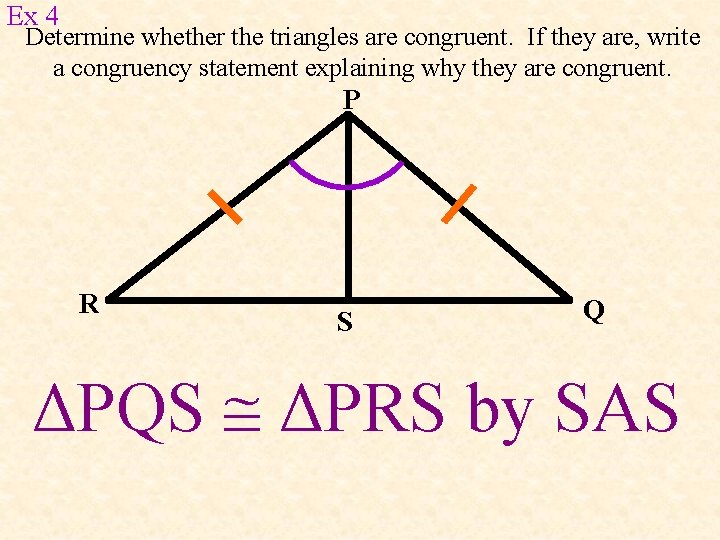
Ex 4 Determine whether the triangles are congruent. If they are, write a congruency statement explaining why they are congruent. P R S Q ΔPQS ΔPRS by SAS

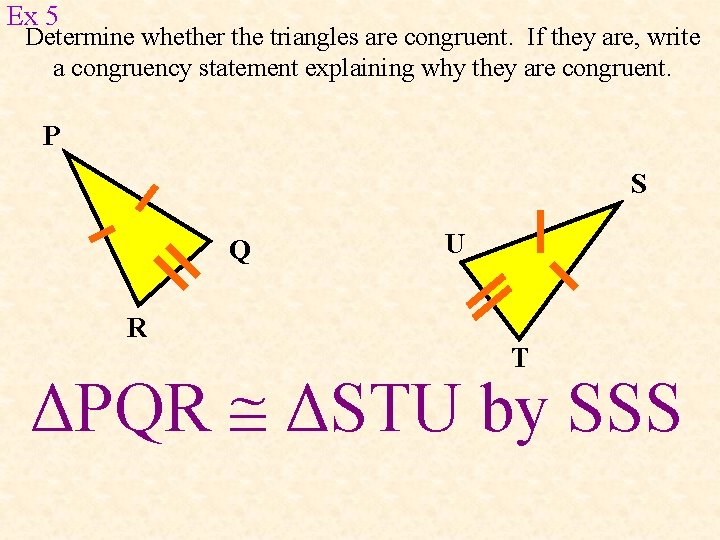
Ex 5 Determine whether the triangles are congruent. If they are, write a congruency statement explaining why they are congruent. P S Q R U T ΔPQR ΔSTU by SSS

Ex 6 Determine whether the triangles are congruent. If they are, write a congruency statement explaining why they are congruent. M P R N Q Not congruent. Not enough Information to Tell

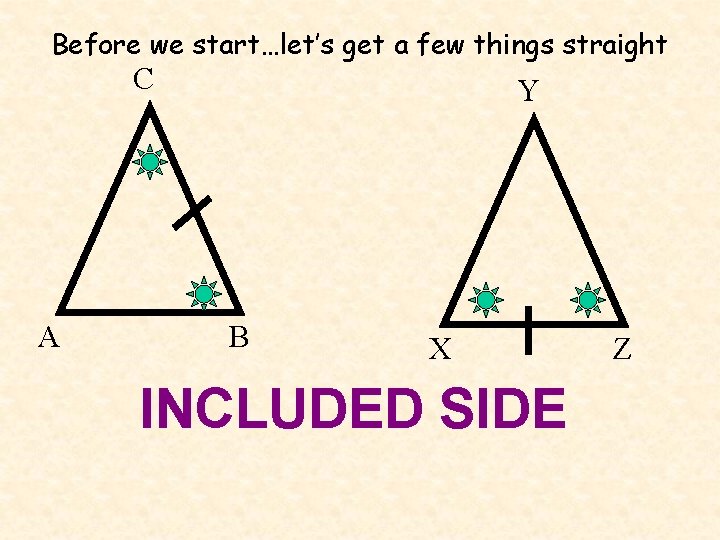
Before we start…let’s get a few things straight C A Y B X INCLUDED SIDE Z

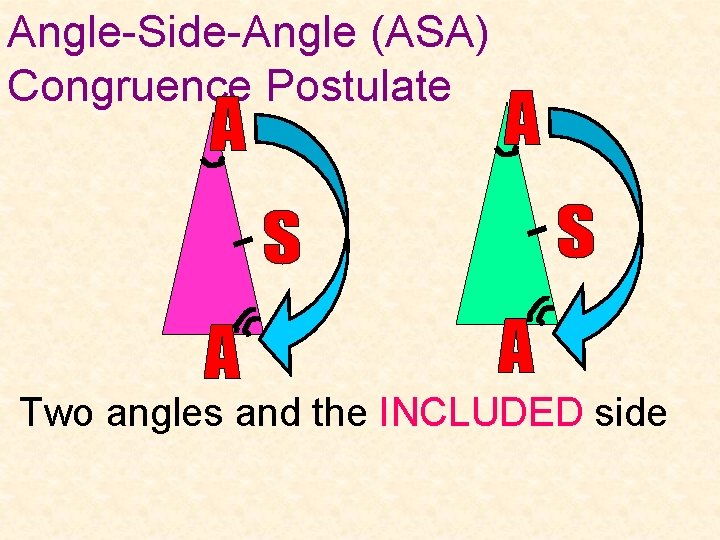
Angle-Side-Angle (ASA) Congruence Postulate Two angles and the INCLUDED side

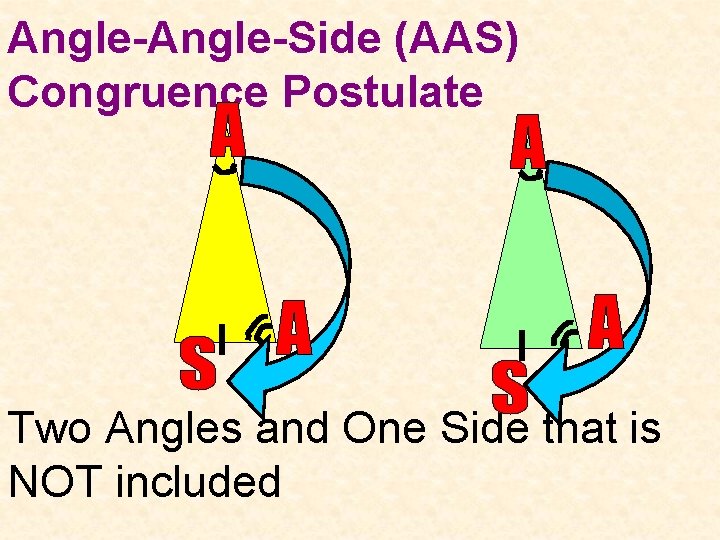
Angle-Side (AAS) Congruence Postulate Two Angles and One Side that is NOT included

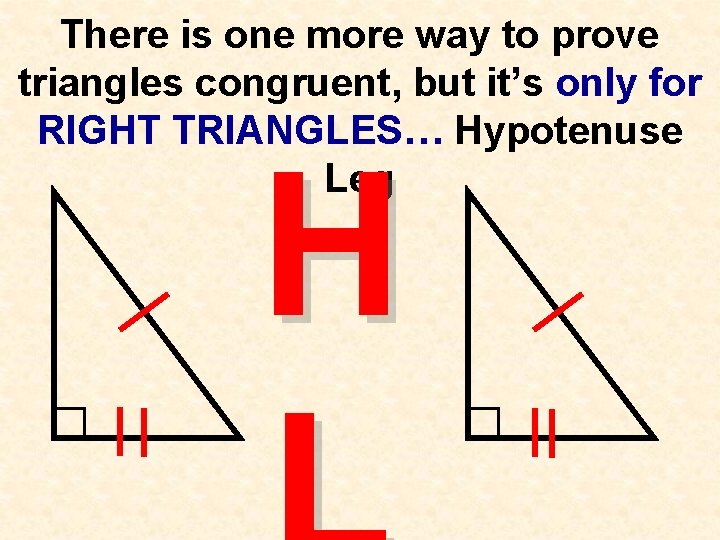
There is one more way to prove triangles congruent, but it’s only for RIGHT TRIANGLES… Hypotenuse Leg H

NO BAD WORDS Your Only Ways To Prove Triangles Are Congruent

Ex 1 DEF NLM ASA by ____

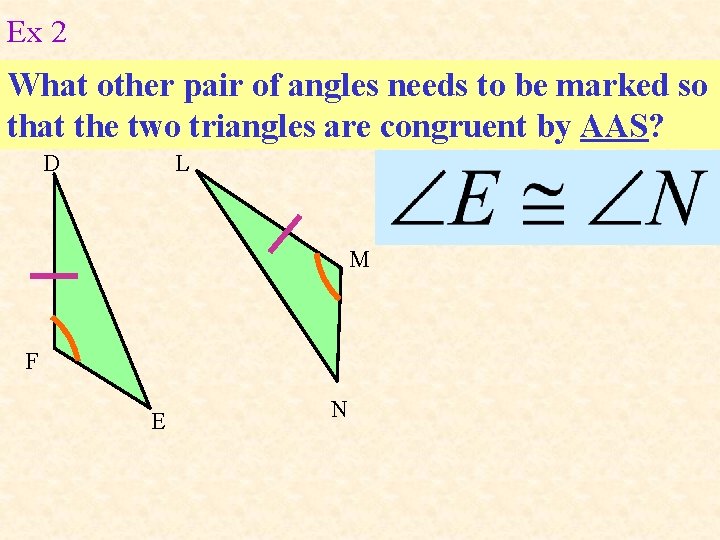
Ex 2 What other pair of angles needs to be marked so that the two triangles are congruent by AAS? D L M F E N

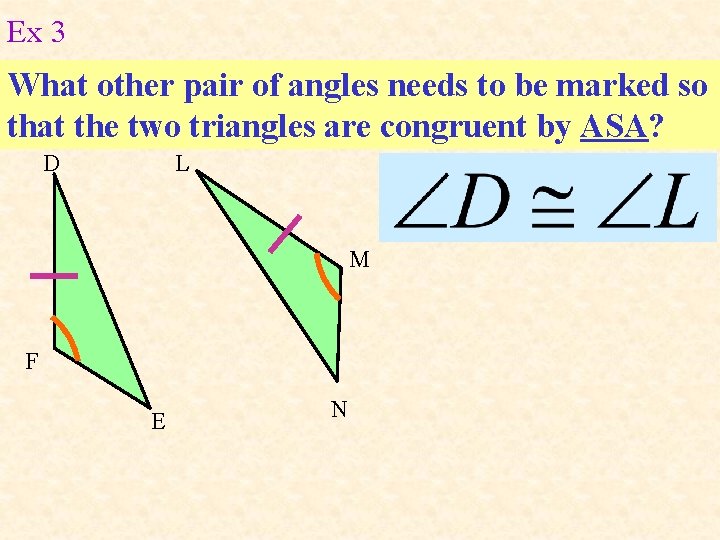
Ex 3 What other pair of angles needs to be marked so that the two triangles are congruent by ASA? D L M F E N

Determine whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 4 G K I H J ΔGIH ΔJIK by AAS

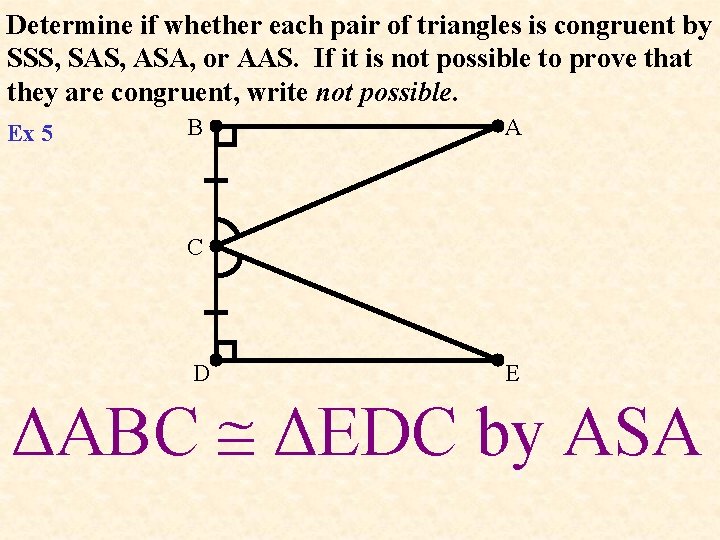
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 5 B A C D E ΔABC ΔEDC by ASA

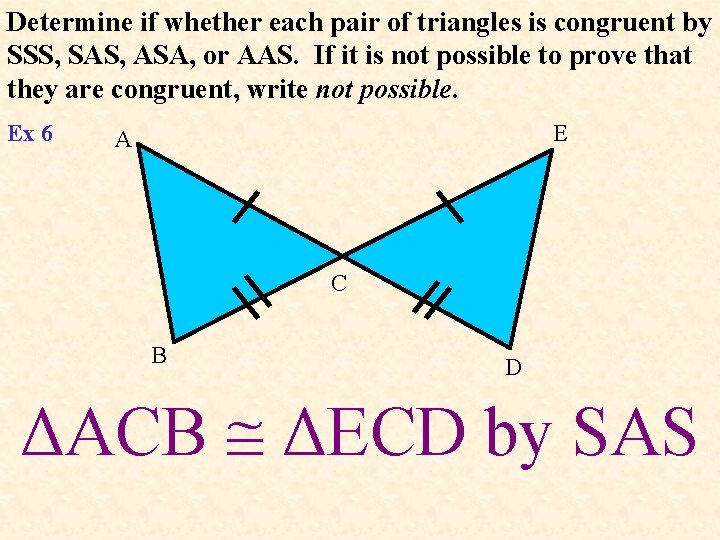
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 6 E A C B D ΔACB ΔECD by SAS

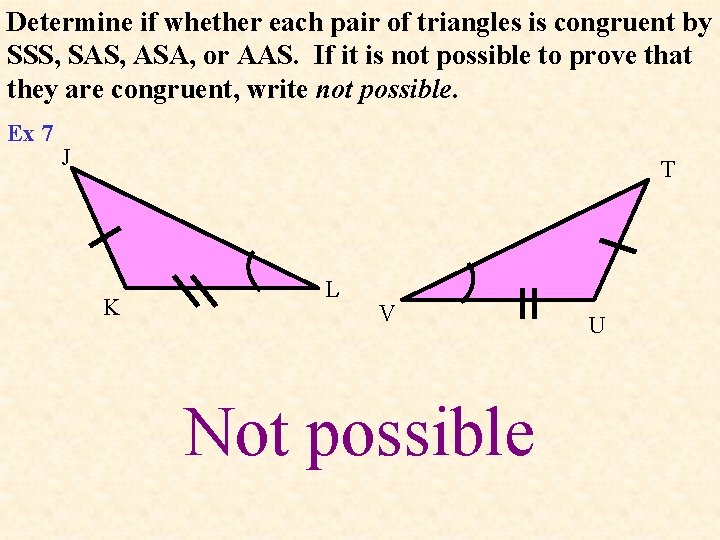
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 7 J T K L V Not possible U