SESSION 3 STIFFNESS MATRIX FOR BRIDGE FOUNDATION AND

SESSION # 3 STIFFNESS MATRIX FOR BRIDGE FOUNDATION AND SIGN CONVETIONS

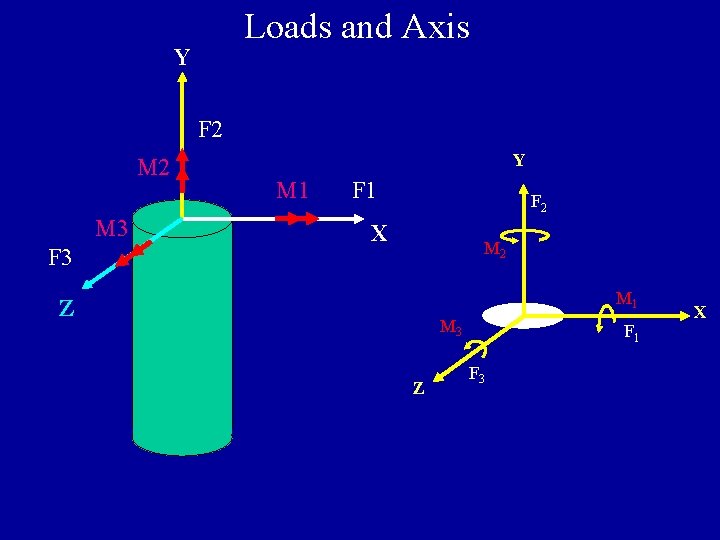
Loads and Axis Y F 2 M 3 F 3 Y M 1 F 2 X M 2 M 1 Z M 3 Z F 1 F 3 X

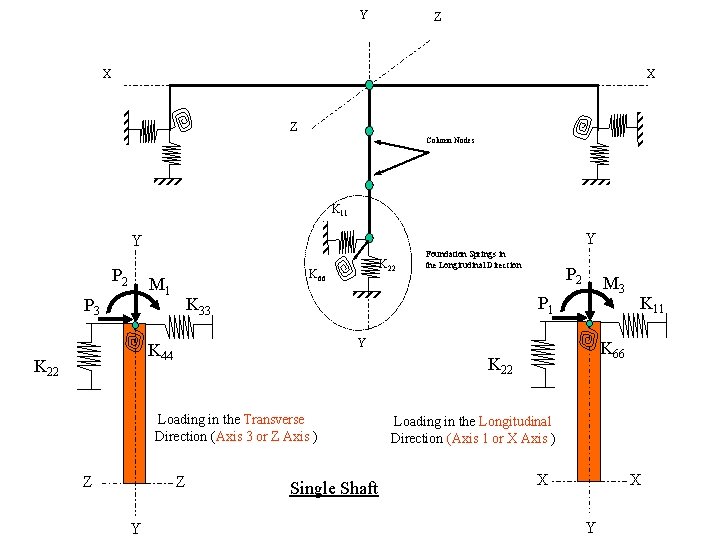
Y Z X X Z Column Nodes K 11 Y Y P 2 M 1 P 3 Single Shaft K 11 K 66 K 22 Z Y M 3 Y Loading in the Transverse Direction (Axis 3 or Z Axis ) Z P 2 P 1 K 33 K 44 K 22 K 66 Foundation Springs in the Longitudinal Direction Loading in the Longitudinal Direction (Axis 1 or X Axis ) X X Y

Steps of Analysis • Using SEISAB, calculate the forces at the base of the fixed column (Po, Mo, Pv) • Use S-SHAFT with special shaft head conditions to calculate the stiffness elements of the required stiffness matrix • Longitudinal (X-X) • KF 1 F 1 = K 11 = Po / (fixed-head, = 0) • KM 3 F 1 = K 61 = MInduced / • KM 3 M 3 = K 66 = Mo / • KF 1 M 3 = K 16 = PInduced / (free-head, = 0)

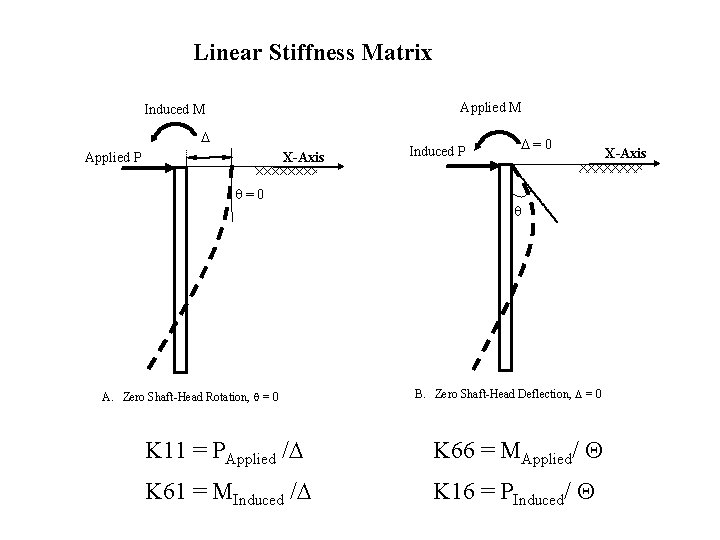
Linear Stiffness Matrix Applied M Induced M Applied P X-Axis =0 A. Zero Shaft-Head Rotation, = 0 Induced P =0 B. Zero Shaft-Head Deflection, = 0 K 11 = PApplied / K 66 = MApplied/ K 61 = MInduced / K 16 = PInduced/ X-Axis

Steps of Analysis F 1 1 2 3 • KF 1 F 1 0 0 -KM 3 F 1 F 2 0 KF 2 F 2 0 0 F 3 M 1 0 0 KF 3 F 3 KF 3 M 1 KM 1 F 3 KM 1 M 1 0 0 M 2 0 0 KM 2 M 2 0 M 3 -KF 1 M 3 0 0 KM 3 M 3 Using SEISAB and the above spring stiffnesses at the base of the column, determine the modified reactions (Po, Mo, Pv) at the base of the column (shaft head)

Steps of Analysis • Keep refining the elements of the stiffness matrix used with SEISAB until reaching the identified tolerance for the forces at the base of the column Why KF 3 M 1 KM 1 F 3 ? KF 3 M 1 = K 34 = F 3 / 1 and KM 1 F 3 = K 43 = M 1 / 3 Does the linear stiffness matrix represent the actual behavior of the shaft-soil interaction?

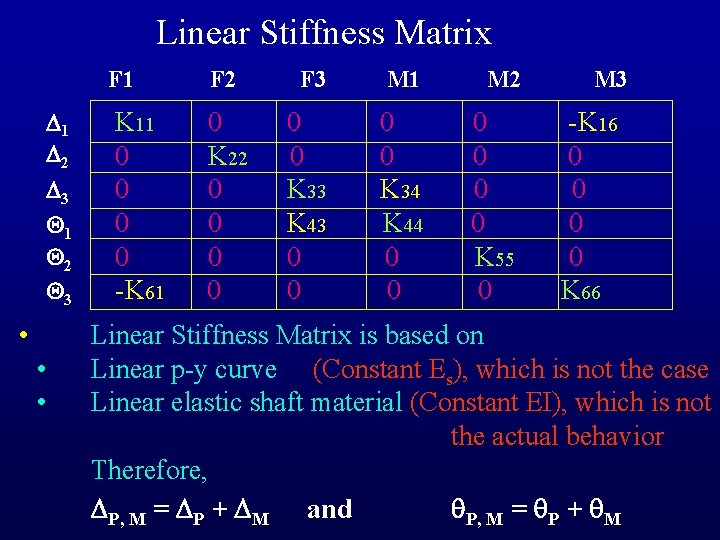
Linear Stiffness Matrix F 1 1 2 3 • • • K 11 0 0 -K 61 F 2 F 3 M 1 M 2 0 K 22 0 0 0 K 33 K 43 0 0 K 34 K 44 0 0 0 K 55 0 M 3 -K 16 0 0 K 66 Linear Stiffness Matrix is based on Linear p-y curve (Constant Es), which is not the case Linear elastic shaft material (Constant EI), which is not the actual behavior Therefore, P, M = P + M and P, M = P + M

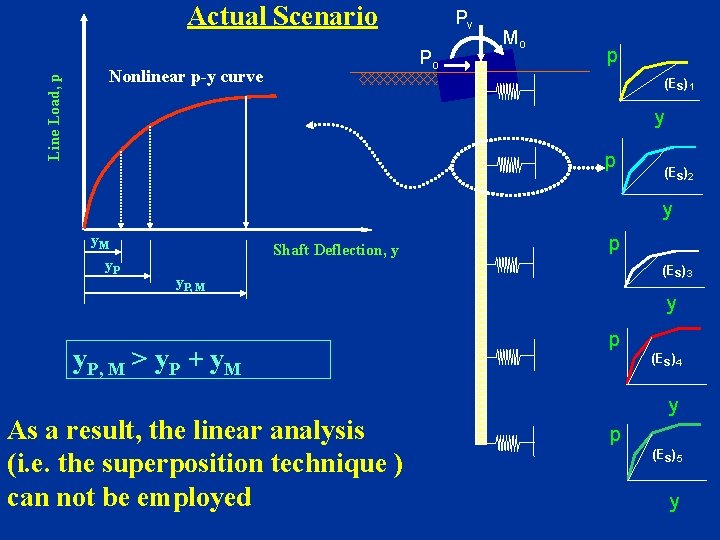
Actual Scenario Po Nonlinear p-y curve Line Load, p Pv Mo p (Es)1 y p (Es)2 y y. M y. P Shaft Deflection, y p (Es)3 y. P, M > y. P + y. M As a result, the linear analysis (i. e. the superposition technique ) can not be employed y p (Es)4 y p (Es)5 y

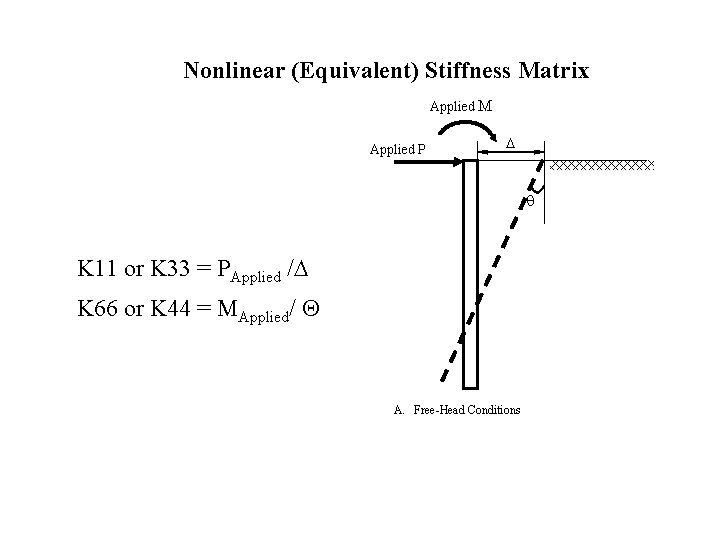
Nonlinear (Equivalent) Stiffness Matrix Applied M Applied P K 11 or K 33 = PApplied / K 66 or K 44 = MApplied/ A. Free-Head Conditions

Nonlinear (Equivalent) Stiffness Matrix F 1 1 2 3 K 11 0 0 0 • • • F 2 F 3 M 1 M 2 0 K 22 0 0 0 K 33 0 0 0 K 44 0 0 0 K 55 0 Nonlinear Stiffness Matrix is based on Nonlinear p-y curve Nonlinear shaft material (Varying EI) P, M > P + M M 3 0 0 0 K 66

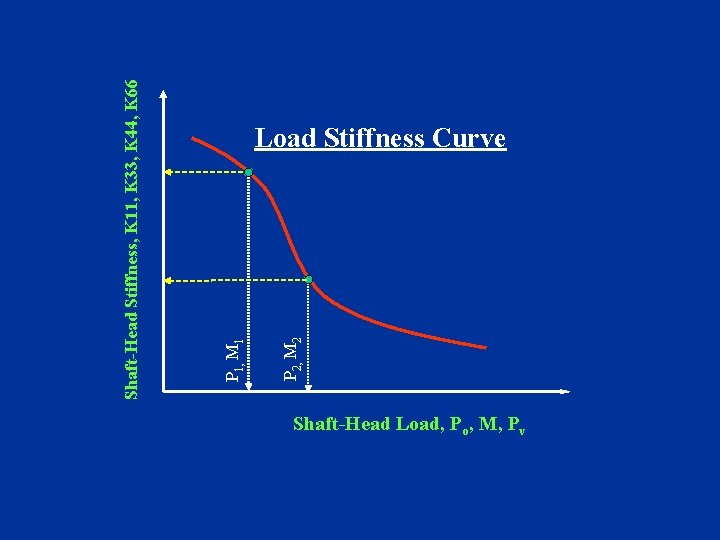
P 2, M 2 P 1, M 1 Shaft-Head Stiffness, K 11, K 33, K 44, K 66 Load Stiffness Curve Shaft-Head Load, Po, M, Pv

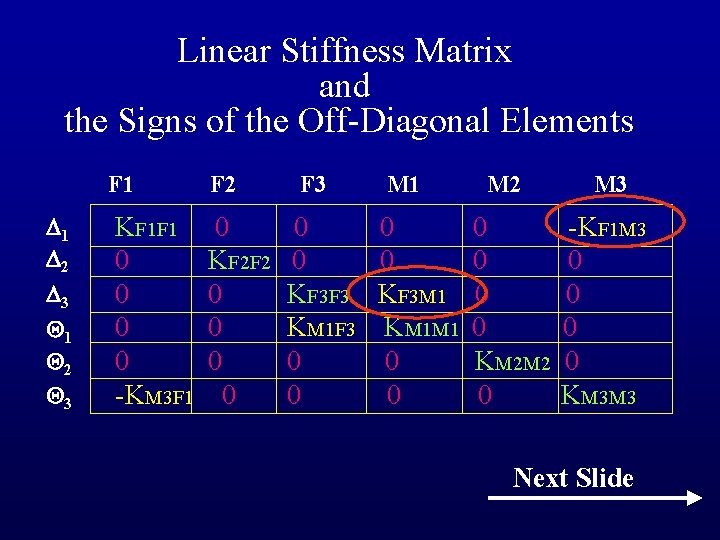
Linear Stiffness Matrix and the Signs of the Off-Diagonal Elements F 1 1 2 3 KF 1 F 1 0 0 -KM 3 F 1 F 2 0 KF 2 F 2 0 0 F 3 M 1 0 0 KF 3 F 3 KF 3 M 1 KM 1 F 3 KM 1 M 1 0 0 M 2 0 0 KM 2 M 2 0 M 3 -KF 1 M 3 0 0 KM 3 M 3 Next Slide

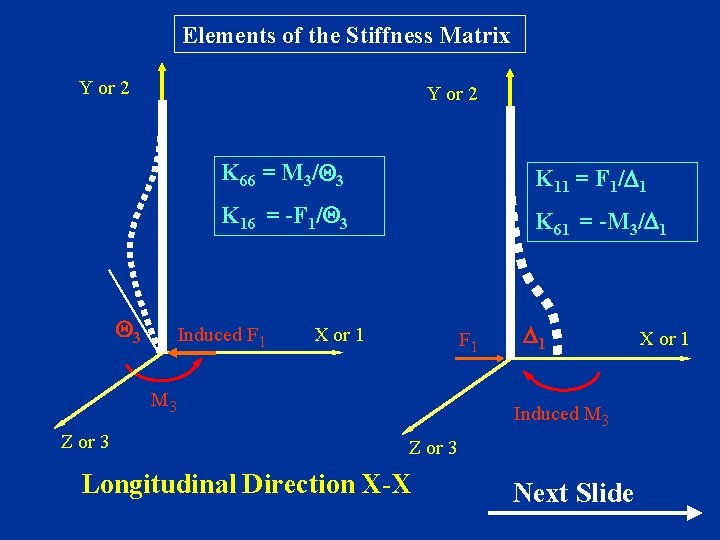
Elements of the Stiffness Matrix Y or 2 3 K 66 = M 3/ 3 K 11 = F 1/ 1 K 16 = -F 1/ 3 K 61 = -M 3/ 1 Induced F 1 X or 1 F 1 M 3 Z or 3 1 Induced M 3 Z or 3 Longitudinal Direction X-X Next Slide X or 1

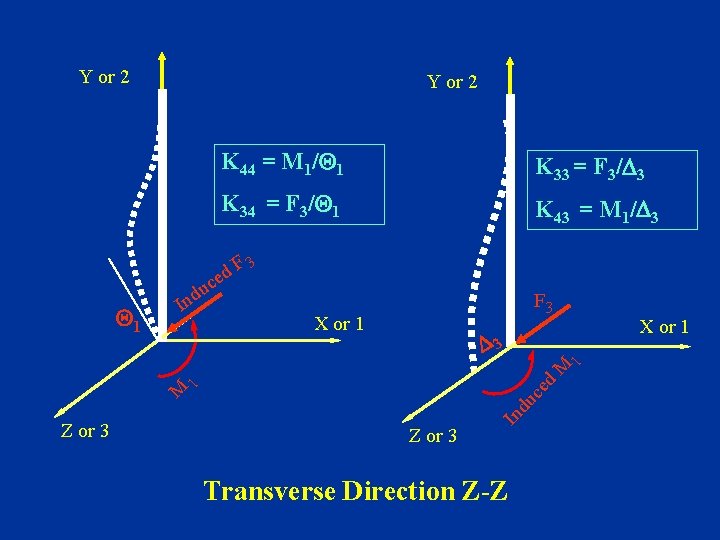
Y or 2 K 34 = F 3/ 1 K 43 = M 1/ 3 3 F 3 X or 1 3 Z or 3 In du ce M 1 d M 1 1 K 33 = F 3/ 3 F d e c u d n I K 44 = M 1/ 1 Transverse Direction Z-Z

MODELING OF INDIVIDUAL SHAFTS AND SHAFT GROUPS WITH/WITHOUT SHAFT CAP

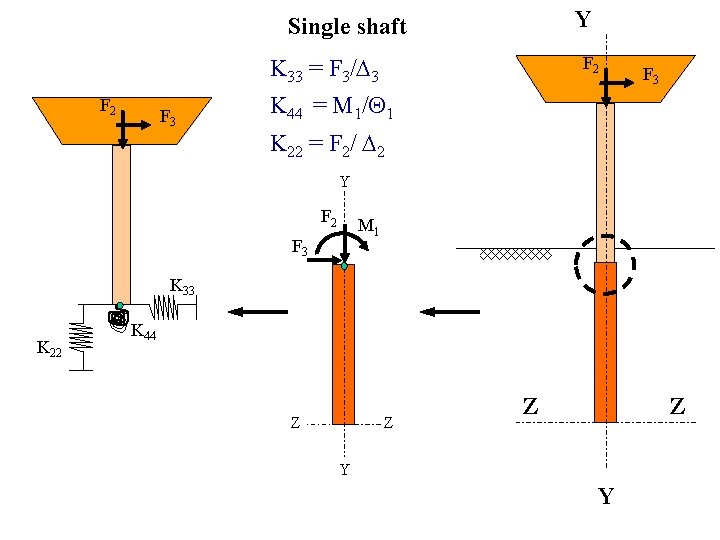
Y Single shaft F 2 K 33 = F 3/ 3 F 2 F 3 K 44 = M 1/ 1 K 22 = F 2/ 2 Y F 2 M 1 F 3 K 33 K 22 K 44 Z Z Y Y

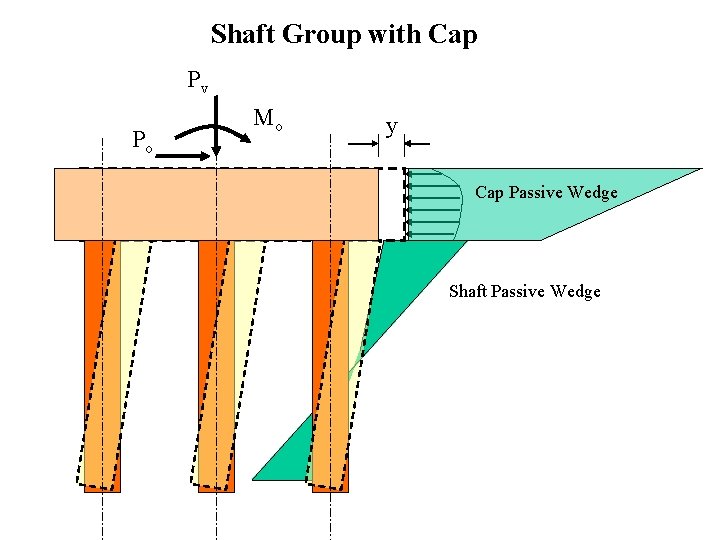
Shaft Group with Cap Pv Po Mo y Cap Passive Wedge Shaft Passive Wedge

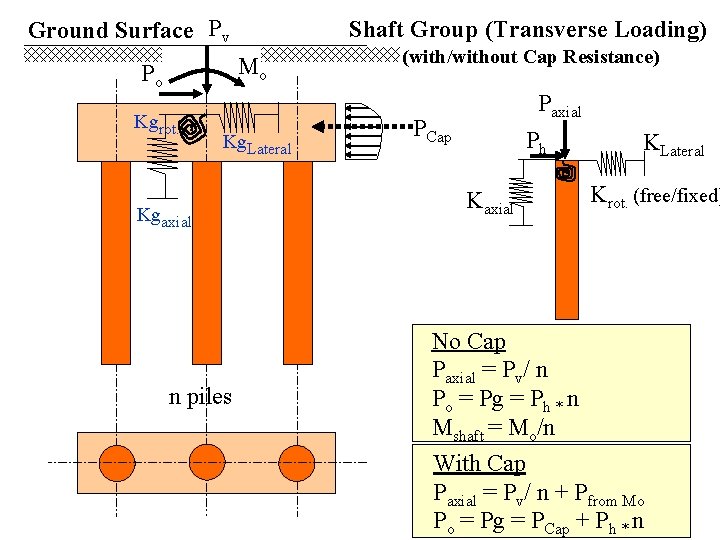
Ground Surface Pv Shaft Group (Transverse Loading) Mo Po Kgrot. Kg. Lateral Kgaxial n piles (with/without Cap Resistance) Paxial PCap Ph Kaxial KLateral Krot. (free/fixed) No Cap Paxial = Pv/ n Po = Pg = Ph * n Mshaft = Mo/n With Cap Paxial = Pv/ n + Pfrom Mo Po = Pg = PCap + Ph * n

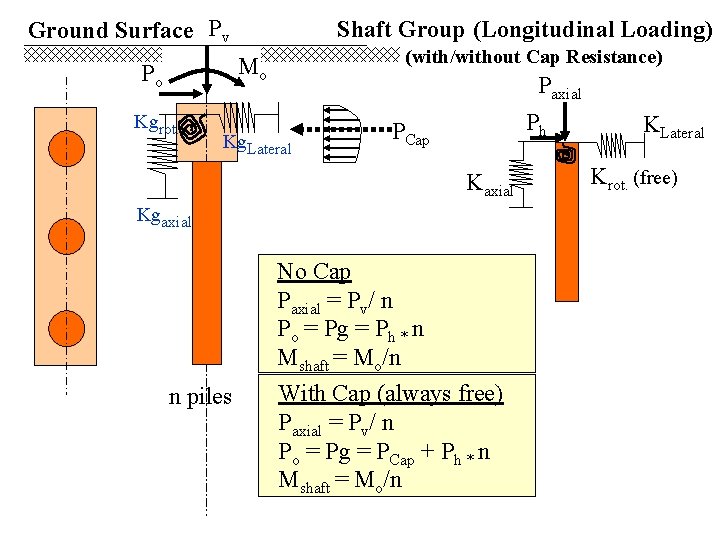
Ground Surface Pv Shaft Group (Longitudinal Loading) (with/without Cap Resistance) Mo Po Kgrot. Paxial Kg. Lateral Ph PCap Kaxial Kgaxial n piles No Cap Paxial = Pv/ n Po = Pg = Ph * n Mshaft = Mo/n With Cap (always free) Paxial = Pv/ n Po = Pg = PCap + Ph * n Mshaft = Mo/n KLateral Krot. (free)

SHAFT GROUP EXAMPLE PROBLEMS

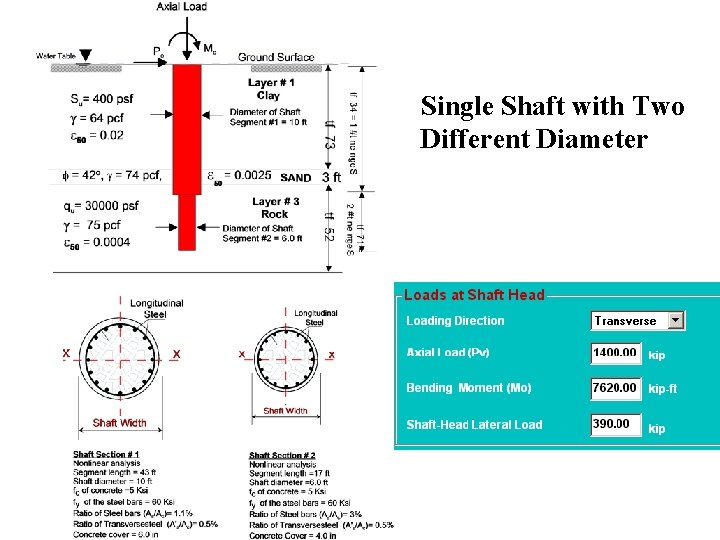
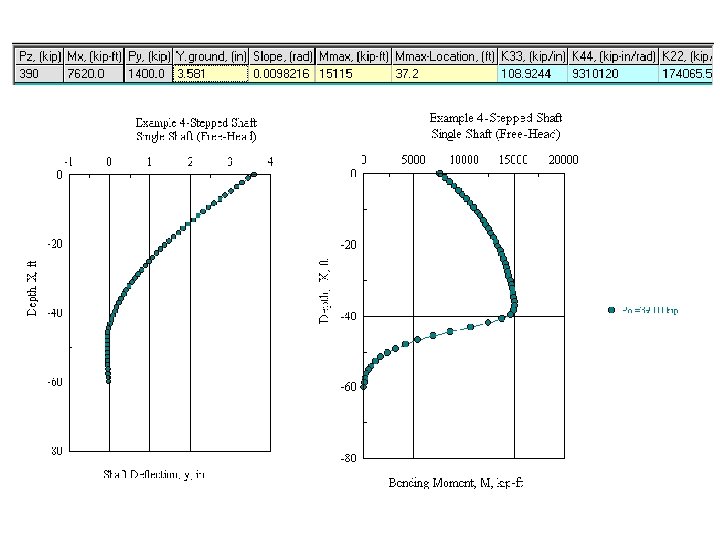
Single Shaft with Two Different Diameter

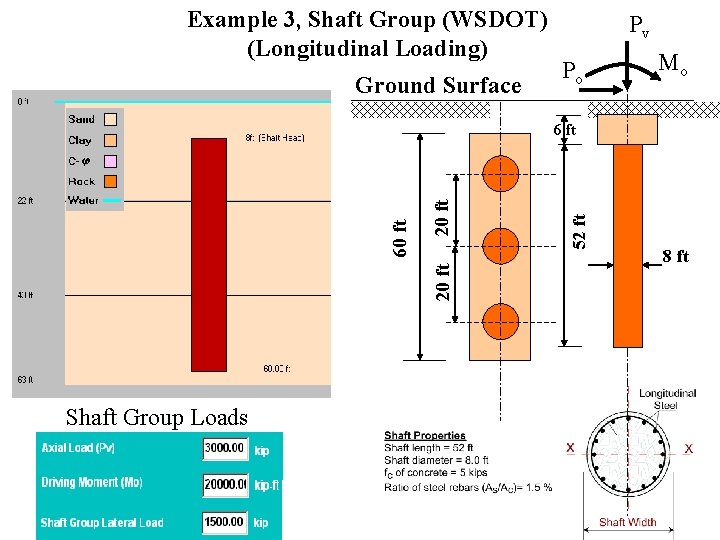
Example 3, Shaft Group (WSDOT) (Longitudinal Loading) Ground Surface Pv Po Mo Shaft Group Loads 52 ft 20 ft 60 ft 6 ft 8 ft

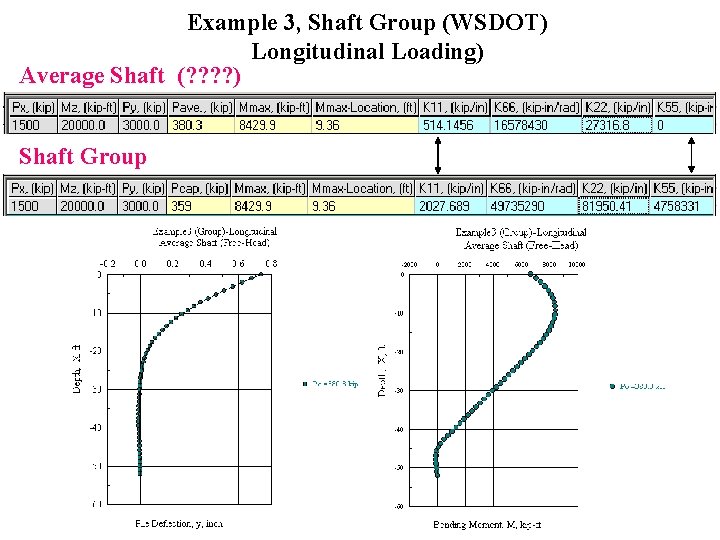
Example 3, Shaft Group (WSDOT) Longitudinal Loading) Average Shaft (? ? ) Shaft Group

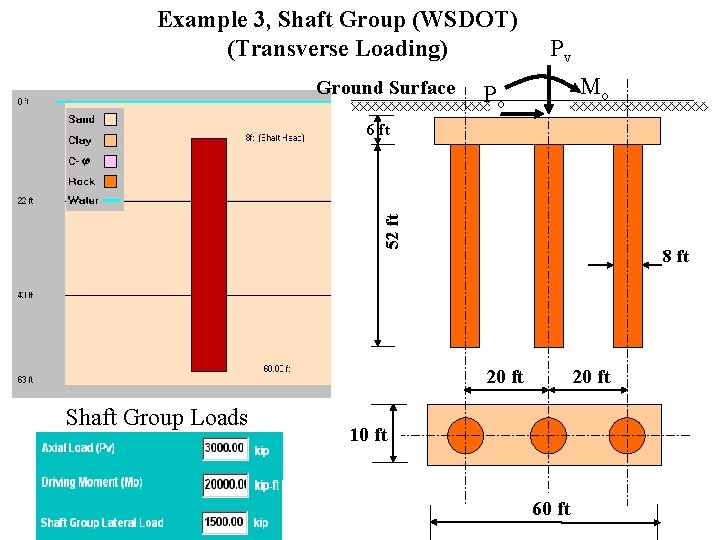
Example 3, Shaft Group (WSDOT) (Transverse Loading) Ground Surface Pv Mo Po 52 ft 6 ft 8 ft 20 ft Shaft Group Loads 20 ft 10 ft 60 ft

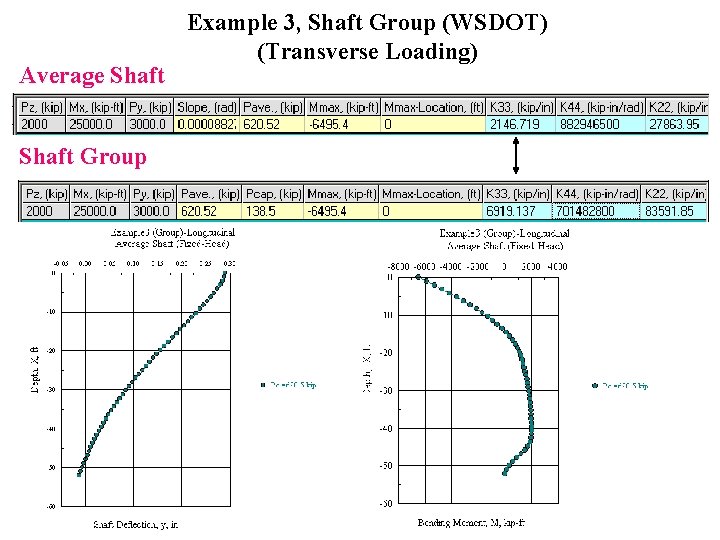
Average Shaft Group Example 3, Shaft Group (WSDOT) (Transverse Loading)

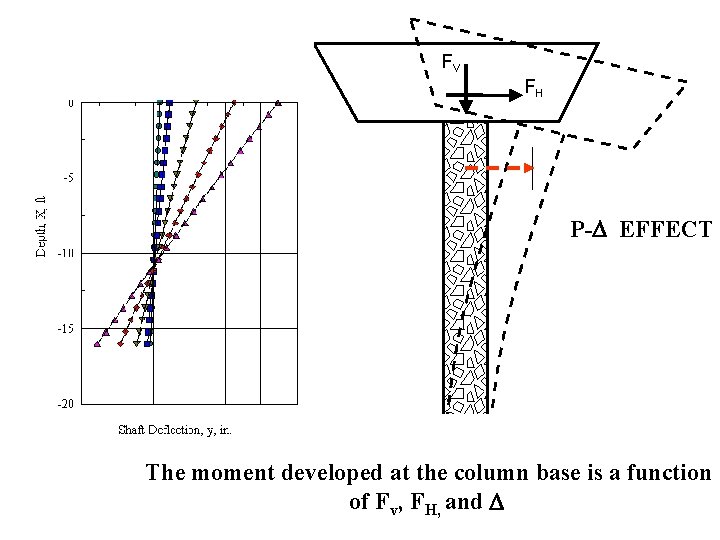
FV FH P- EFFECT KH The moment developed at the column base is a function of FKv 1, FH, and K 2