Session 3 Calculating with Fractions Decimals and Percentages


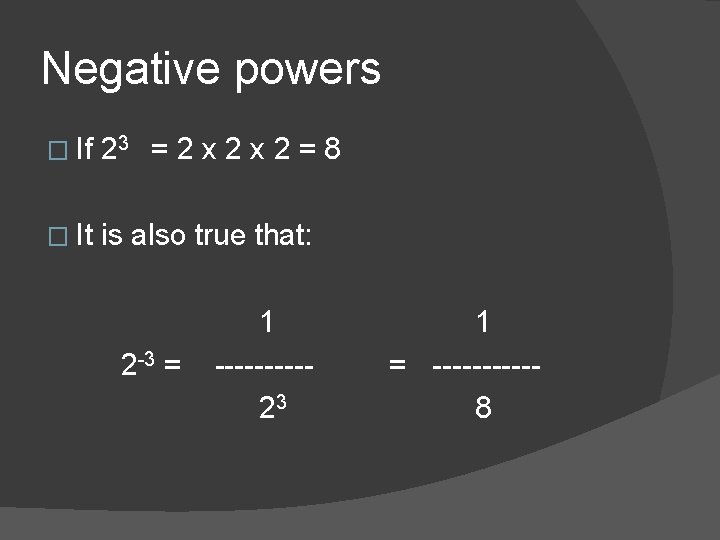


















- Slides: 21

Session 3 – Calculating with Fractions, Decimals and Percentages (non-calculator) GCSE MATHS

Rules of Indices
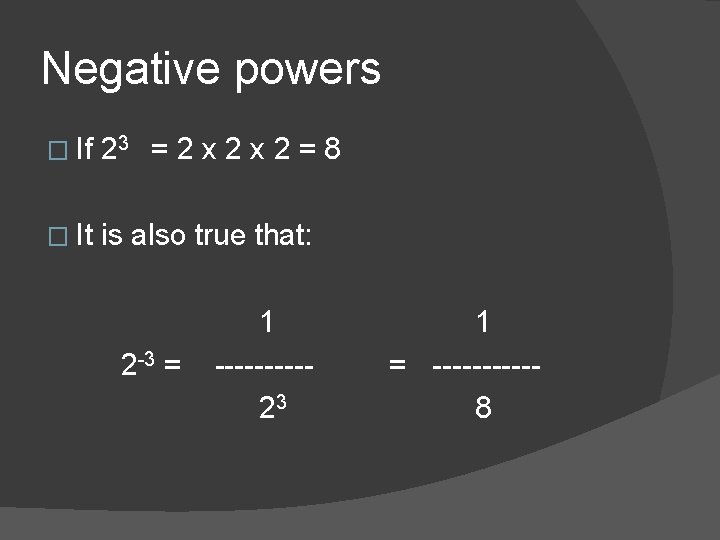
Negative powers � If 23 = 2 x 2 = 8 � It is also true that: 2 -3 = 1 -----23 1 = -----8

Reciprocals The reciprocal of 2 = ½ The reciprocal of 4 = ¼ 1 The reciprocal of am = ------ = a -m am

� Everyone must make a note of the first 4 rules and know how to use them. The 5 th and 6 th rules are on higher tier only.

Decimals � Adding decimals is the same as adding integers, just keep the columns and the decimal point in line � The same rules apply to subtraction Exercise 2. 1 � Question 4 a and 4 e � Extension 4 c and 4 g

Multiplying decimals � Remove the decimal points and just multiply the digits as normal, lining them up from right to left. � Put the decimals back into the question and count how may digits after the point in both numbers together � Add the decimal point to the answer the same number of places in

Example � To calculate 3. 42 × 2 we work out 342 × 2 � Then point. � In work out where to put the decimal this case, 2 decimal plaves in the question, so 2 decimal places in the answer.

Dividing decimals � Dividing a decimal into an integer: Divide as usual, keeping the decimal point aligned Dividing into a decimal Multiply by 10, 100 to make it an integer, then multiply the number to be divided by the same.

Examples (from book) � Exercise 2. 2 � Questions 9 and 11 � Extension – continue from question 11.

Numerical calculations with a calculator � Write down the calculations, only change one thing at a time � Apply the rules of Bo. DMAS � Exercise 2. 3 Question 1 � Extension Questions 2, 3, 5

Fractions � Numerator over denominator (this is also how you change to decimal) � To write equivalent fractions, multiply or divide the top and bottom by the same number. � Cancelling down fractions is to write them using the smallest numbers possible

� Mixed numbers contain integers and fractions � Top heavy fractions are also called improper fractions � Exercise 2. 4 Questions 2 -8

Fractions of quantities � Consider how you would break a shape into 2/5 � Divide by the bottom of the fraction and multiply by the top

� Exercise 2. 4 Questions 9 – 13 Extension 14

Adding and Subtracting Fractions � Fractions mush have the same denominator in order to add or subtract them. � To do this we must find a common denominator � Change the fractions to equivalent fractions with the same denominator � Add or Subtract the numerators, keeping the denominators the same.

� Exercise 2. 5 Questions 1 - 6 a Extension Q 1 - 6 e Then Q 7 - 10

Multiplying Fractions � Multiply the numerators � Multiply the denominators � Simplify the fraction � Exercise 2. 6 Question 2 � Extension Question 5

Dividing Fractions � Turn the fraction on the right of the divide sign upside down � Change the divide sign to a multiply and compleat the question as you would with multiplication � Exercise 2. 7 Q 1 a, b, c Q 3 a, b, c � then Q 6, Q 7, Q 8

Fractions on a calculator � Fractions button, mixed number button � Fractions to decimals � Top number divided by the bottom number � Exercise 2. 9 – a few questions

Homework � Complete Review Exercise 2 for Homework, mark it using the answers at the back of the book, and bring it with you next week.