SESSION 2 DIRECT LOADED CONNECTIONS PRYING FORCES BOLT

SESSION 2 DIRECT LOADED CONNECTIONS PRYING FORCES BOLT AND WELD ECCENTRICITY 1

DIRECT LOADED TENSION CONNECTION 5/16 2 L 4 x 3 1/2 x 1/4 LLBB 5/8" PL Tn 2

DIRECT LOADED TENSION CONNECTION LIMIT STATES • • Tension Yielding Tension Rupture Block Shear Bearing and Tear Out (Session 1) Bolt Rupture (Session 1) Weld Rupture (Session 1) Whitmore Section Considerations 3

Tension Yielding Actually a member limit state. Fy Tn Tn = 0. 9 Fy Ag For design Tu < Tn (T < Tn / ) 4

Tension Rupture Tn = 0. 75 Fu Ae Fu = tensile strength = 58 ksi for A 36; 65 ksi for A 992 & Gr 50 Ae = effective net area = U An U = reduction or shear lag coefficient An = net area 5

Tension Rupture Reduction or Shear Lag Coefficient (LRFD Chapter B 3) U = 1 – x¯ / L < 0. 9 L L c. g. + 6

Tension Rupture Shear Lag: 7

Tension Rupture An = Net Area = Ag – Ah + Stagger Ag = gross area of cross-section Ah = area of hole = (hole diameter + 1/16 in. ) tp Stagger = (s 2/4 g)tp Note: An < 0. 85 Ag for Tension Plates (Rule does not apply to members) 8

Tension Rupture Stagger Term = (s 2/4 g)tp g Tu s g g Tu 9

Block Shear • Failure occurs when larger force reaches the rupture strength. • Smaller force may be yield or rupture. 10

11

Block Shear Section J 4. 3 Block Shear Rupture Strength (1999 LRFD Specification) When Fu Ant > 0. 6 Fu. Anv: Rn = [0. 6 Fy. Agv+Fu. Ant] < [0. 6 Fu. Anv +Fu. Ant] When Fu Ant < 0. 6 Fu. Anv: Rn = [0. 6 Fu. Anv+Fy. Agt] < [0. 6 Fu. Anv +Fu. Ant] = 0. 75 12

Block Shear Rn = Ten. Rupture Opp. Yield + max Shear Rupture min Opp. Rupture Tension Rupture Shear Rupture = Fu. Ant = 0. 6 Fu. Anv Tension Yield Shear Yield = Fy. Agt = 0. 6 Fy. Agv 13

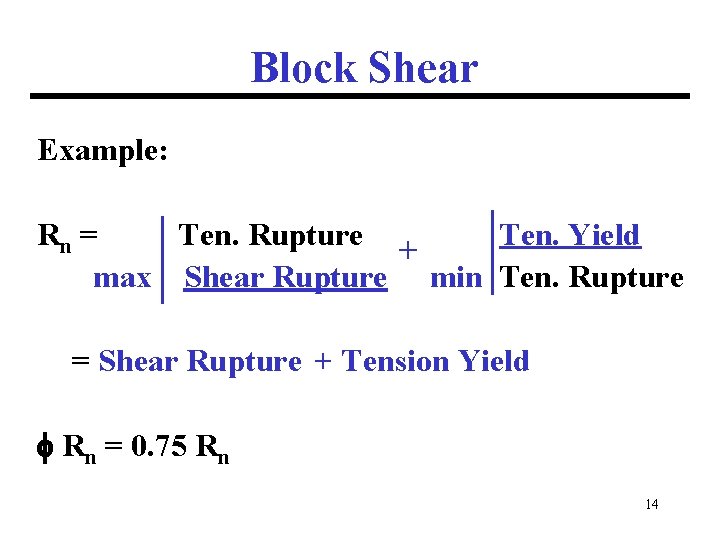
Block Shear Example: Rn = Ten. Rupture Ten. Yield + max Shear Rupture min Ten. Rupture = Shear Rupture + Tension Yield Rn = 0. 75 Rn 14

Block Shear Example: Ant= 0. 781 in 2 Agt= 1. 0 in 2 Anv= 2. 53 in 2 Agv= 3. 625 in 2 A 36 Steel: Fy = 36 ksi Fu = 58 ksi Rn = 58 x 0. 781=45. 3 36 x 1. 0=36. 0 + max 0. 6 x 58 x 2. 53=88. 0 min 45. 3 = 88. 0 + 36. 0 = 124. 0 k Rn = 0. 75 x 124. 0 = 93. 0 k (Note: See following example for area calculations) 15

Block Shear Welded Connections Tu Tension Area Shear Area 16

Whitmore Section 30° Critical Section Tu 30° 17

Whitmore Section 18

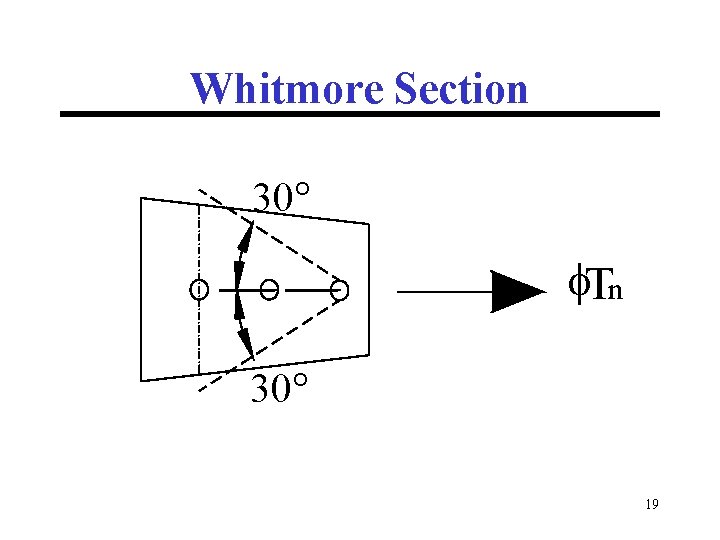
Whitmore Section 30° Tn 30° 19

LIGHT BRACING CONNECTION Example. Determine Tn. 5/16 5/8" PL 7" A 36 Steel 3/4 in. A 325 -N Bolts A Tn 5" 2" 2 L 4 x 3 1/2 x 1/4 LLBB Ag = 3. 62 in. 2 x = 0. 909 in. A 114 " 3" 3" 114 " Section A-A 20

2 1 3 4 T n 2 1 Limit States: Angles: 1. Tension Yield 2. Tension Rupture 3. Bearing and Tear Out 4. Block Shear 21

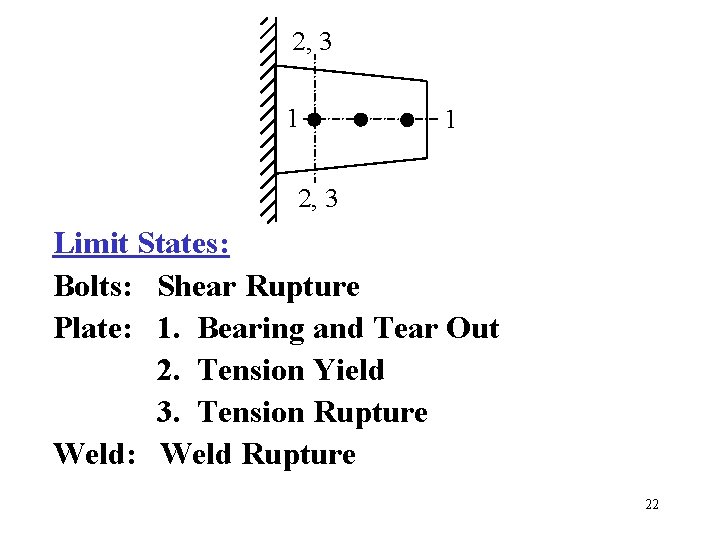
2, 3 1 1 2, 3 Limit States: Bolts: Shear Rupture Plate: 1. Bearing and Tear Out 2. Tension Yield 3. Tension Rupture Weld: Weld Rupture 22

2 L 4 x 3 1/2 x ¼ LLBB Ag = 3. 62 in. 2 Tn Angle Yielding: Tn = 0. 9 Fy Ag = 0. 9 x 36 x 3. 62 = 117. 3 k (Tn/ = 36 x 3. 62 / 1. 67 = 78. 0 k) LRFD ASD 23

L 2 L 4 x 3 1/2 x ¼ LLBB Tn x = 0. 909 in. Angle Rupture: Tn = 0. 75 Fu Ae = 0. 75 Fu UAn An = Ag-Ah = 3. 62 – (0. 5) (3/4 + 1/16) = 3. 18 in 2 U = 1 - x/L = 1 – 0. 909/6 = 0. 849 < 0. 9 Tn = 0. 75 x 58 x 0. 849 x 3. 18 = 117. 4 k (Tn/ = 58 x 0. 849 x 3. 18 / 2. 0 = 78. 3 k) 24

Lc Lc 2 L 4 x 3 1/2 x ¼ LLBB Tn Angle Bearing / Tear Out (From Session 1) Bearing: 2. 4 Futd = (2. 4 x 58) (0. 5 x 3/4) = 52. 2 k Edge: 1. 2 Fu. Lct = (1. 2 x 58) (1. 25 - 13/32) (0. 5) = 29. 4 k < 52. 2 k Other: 1. 2 Fu. Lct = (1. 2 x 58) (3. 0 - 13/16) (0. 50) = 76. 1 k > 52. 2 k 25

2 L 4 x 3 1/2 x ¼ LLBB Tn Angle Bearing / Tear Out (From Session 1) Tn = 0. 75 (1 x edge + 2 x other) = 0. 75 ( 29. 4 + 2 x 52. 2) = 100. 4 k (Tn/ = (29. 4 + 2 x 52. 2) / 2. 0 = 66. 9 k) 26

Agv , Anv 2 L 4 x 3 1/2 x ¼ LLBB Tn 2" 114" 3" 3" Agt , Ant Angle Block Shear: Agv = 0. 5 x 7. 25 = 3. 625 in 2 Anv = 0. 5 [7. 25 - (2. 5 x 7/8)] = 2. 53 in 2 Agt = 0. 5 x 2. 0 = 1. 0 in 2 Ant = 0. 5 [2. 0 – (0. 5 x 7/8)] = 0. 781 in 2 27

A gv, A nv 2 L 4 x 3 1/2 x ¼ LLBB Tn 2" 114 " 3" 3" Ten. Rupture Opp. Yield max Shear Rupture min Opp. Rupture + Rn = A gt, A nt 58 x 0. 781 = 45. 3 1. 0 x 36 = 36. 0 max 0. 6 x 58 x 2. 53 = 88. 0 + min 45. 3 = Rn = 0. 75 (88. 0 + 36. 0) = 93. 0 k (Rn/ = (88. 0 + 36. 0) / 2. 0 = 62. 0 k)28

2 L 4 x 3 1/2 x 1/4 LLBB Ag = 3. 62 in. 2 x = 0. 909 in. 5/16 5/8" PL 7" 5" 2" 114" 3" 3" Tn 114 " Bolt Rupture: 3 - ¾ in. A 325 -N Bolts in Double Shear With rv = 31. 8 k (double shear) Tn = 3 x 31. 8 = 95. 4 k (Tn/ = 3 x 42. 4 / 2. 0 = 63. 6 k) 29

2 L 4 x 3 1/2 x 1/4 LLBB Ag = 3. 62 in. 2 x = 0. 909 in. 5/16 5/8" PL 7" 5" 2" 114" 3" 3" Tn 114 " Plate Bearing / Tear Out: Plate t = 5/8 in. From angle calculation by proportion: Tn = (0. 625 / 0. 50) (100. 4) = 125. 5 k (Tn/ = (0. 625 / 0. 50) (66. 9) = 83. 6 k) 30

30° 5/8 in. Plate 6. 48 in. Tn 30° Plate Yielding at Whitmore Section: Ag = 0. 625 x 6. 48 = 4. 05 in 2 Tn= 0. 9 Fy Ag = (0. 9 x 36) (4. 05) =131. 2 k (Tn/ = 36 x 4. 05 / 1. 67 = 87. 3 k) 31

30° 5/8 in. Plate 6. 48 in. Tn 30° Plate Rupture at Whitmore Section: Ae = UAn U = 1. 0 for plates An = (6. 48 – 0. 875)(0. 625) = 3. 50 in 2 < 0. 85 Ag = 0. 85(4. 05) = 3. 44 in 2 Tn = 0. 75 Fu Ae = (0. 75 x 58) (1. 0 x 3. 44) = 149. 6 k (Tn/ = 58 (1. 0 x 3. 44) / 2. 0 = 99. 8 k) 32

5/16 30° Tn 7" 30° Weld Rupture: Tn =1. 392 (1. 5) D Lweld = 1. 392 (1. 5) (2 x 5) 7. 0 = 146. 2 k (Tn/ = 0. 928 (1. 5) (2 x 5) 7. 0 = 97. 4 k) 33

2 L 4 x 3 1/2 x 1/4 LLBB Ag = 3. 62 in. 2 x = 0. 909 in. 5/16 5/8" PL 7" 5" 2" 114" 3" 3" Tn 114" Connection Tn = 93. 0 k (Block Shear) (Tn/ = 62. 0 k (Block Shear)) 34

Bolted Hanger Connections 35

Bolted Hanger Connections New Limit States Tee Flange Bending Bolt Tension including Prying Force 36

Bolted Hanger Connections Stages of Flange Plate Behavior qu ru ru 2 ru No Prying ru+qu qu qu ru+qu 2 ru ru+qu qu ru+qu 2 ru Maximum Prying 37

Flange Bending qu = prying force = applied force per 38 bolt line

Flange Bending Mu 1 < Mp No Hinges No Prying Force, qu = 0 39

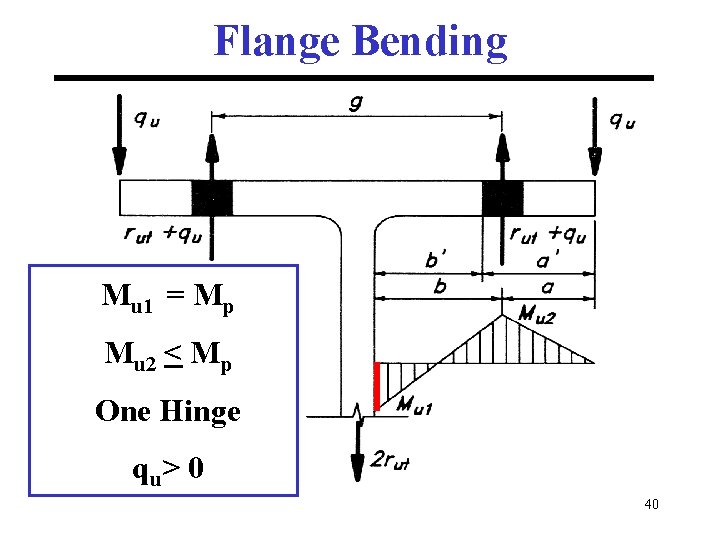
Flange Bending Mu 1 = Mp Mu 2 < Mp One Hinge q u> 0 40

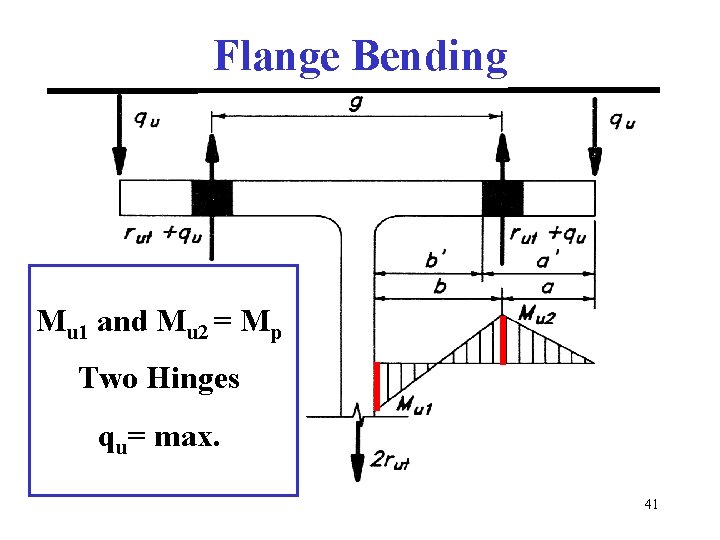
Flange Bending Mu 1 and Mu 2 = Mp Two Hinges qu= max. 41

Flange Bending db = bolt diameter a < 1. 25 b in calcs a = a + db/2 b = b – db/2 =b /a 42

Required Plate Thickness With no prying action: Solving for treq’d: rut = factored force per bolt p = length of hanger per bolt line 43

Required Plate Thickness With prying action: rut = factored force per bolt p = length of hanger per bolt line = 1 - dh / p dh = diameter of bolt hole 44

Required Plate Thickness : If = ( rn/rut-1)/ > 1. 0 then = 1. 0 Otherwise = [ / (1 - ) ] / min 1. 0 45

Bolt Force B = rut + qu = applied force + prying force 46

Bolts: Eccentric Connections Pu Pu M u = Pu e = Elastic Method + 47

Bolts: Eccentric Connections lo e lo Pu e Pu I. C. c. g. I. C. lr m ru max ax Instantaneous Center of Rotation Method 48

49

Example: Determine Pn Pn = C (from Table 8 -19) x rv From Table 8 -19 with e = 8 in. and n=4 C = 2. 93 e = 8" Pn s = 3" rv = Fv. Ab = 15. 9 k/bolt Pn = 2. 93 x 15. 9 = 46. 6 k s = 3" 3" 3/4" A 325 -N Bolts 50

51

Welds: Eccentric Connections Pu Pu = c. g. + c. g. Mu = Pu e Elastic Method 52

Welds: Eccentric Connections lo e lo Pu e Pu I. C. c. g. I. C. c. g. l r ma r u max x Instantaneous Center of Rotation Method 53

54

Example: Determine Pn 6" 8" Pn ex= a. L L = 8" 8" E 70 XX Pn c. g. x. L 5/16 E 70 XX k. L 55

Example: Determine Pn 6" 8" ex = a. L Pn 8" E 70 XX L = 8" Pn c. g. x. L 5/16 E 70 XX k. L = 6 in. k = 6 /8 = 0. 75 Using Table 8 -42: x = 0. 225 x. L = 0. 225 x 8 = 1. 8 in. (location of c. g. ) 56

Table 8 -42 57

Example: Determine Pn With ex= a. L a = (6. 0+8. 0 -1. 8)/8. 0 = 1. 53 Using Table 8 -42: C = 1. 19 D = 5 (since 5/16” weld) C 1 = 1. 0 (since E 70 XX weld) Pn = C C 1 D L = 1. 19 x 1. 0 x 5 x 8. 0 = 47. 6 k 58

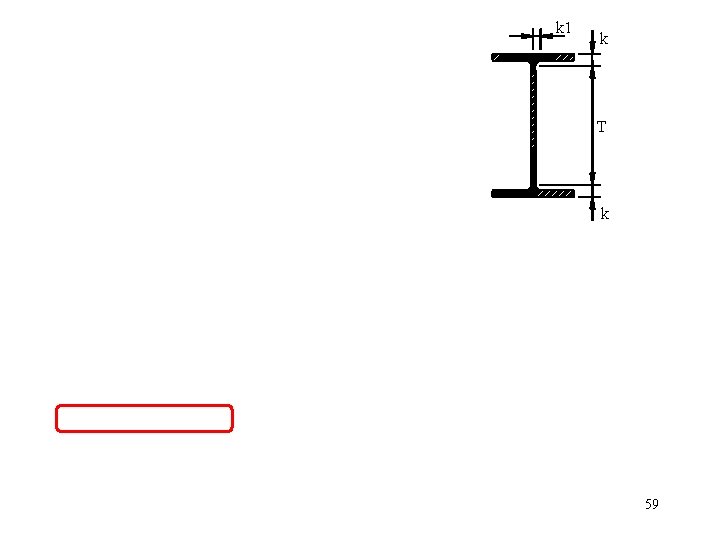
k 1 k T k 59

AISC ADVISORY February 14, 2001 Example: W 14 x 22 kdesign = 0. 735 in. kdetailing = 1 1/16 in. The limit state dictates which value is used in design. 60

END OF SESSION 2 Design Example (For Home Study) 61

HANGER CONNECTION EXAMPLE Determine if the hanger connection shown on the next slide is adequate if: Pu = 80 k. A 992 Steel ¾ in. A 325 Bolts 62

= 8. 0 in. x 8 in. = 80 kips 63

Connection Limit States Tee: Flange Bending, Shear Yielding, Shear Rupture Tension Yielding of the Stem, Block Shear Bolts: Tension Rupture including Prying Beam: Flange Bending 64

Needed Properties W 24 x 94 tf = 0. 875 in. A 992 Fy = 50 ksi WT 8 x 28. 5 bf = 7. 12 in. Fu = 65 ksi tf = 0. 715 in. tw = 0. 430 in. 3/4 in. A 325 Bolts rv = Ft (Table J 3. 2) Ab = 0. 75 x 90 x 0. 4418 = 29. 8 k 65

Calculated Properties p = flange width/bolt = 8. 0/ 2 = 4. 0 in. b = (g - tw)/2 = (4 – 0. 430)/2 = 1. 79 in. a = (bf – g)/2 = (7. 12 – 4)/2 = 1. 56 in. < 1. 25 b b = b – db/2 = 1. 79 – 0. 75/2 = 1. 42 in. a = a + db/2 = 1. 56 + 0. 75/2 = 1. 94 in. = b / a = 1. 42 /1. 94 = 0. 732 = 1 – dh/p = 1 – (13/16)/4 = 0. 797 66

Required Flange Thickness : ru = 80 /4 = 20 k = ( rn/rut-1)/ = (29. 8 / 20 – 1) / 0. 732 = 0. 669 < 1. 0 Therefore, = [ / (1 - ) ] / = [0. 669/(1 -0. 669)]/0. 797 = 2. 54 min 1. 0 = 1. 0 67

Required Flange Thickness = 0. 592 in. < 0. 715 in for the WT 8 x 28. 5 < 0. 875 in for the W 24 x 94 68

Check Bolt Strength (Not required) Bu = rut + qu = applied force + prying force < rn With 69

Check Bolt Strength = 0. 969 in. = 0. 292 > 0 70

Check Bolt Strength Cont. = 2. 76 k/bolt Bu = rut + qu = 20 + 2. 76 = 22. 8 k < rn = 29. 8 k 71

Stem Yielding: Whitmore Section Lcr = 3 + 2 x 4 x tan 30 o = 7. 62 in. < 8 in. 30° Critical Section 2 L 3 x 3 x 5/16 Tu 30° 4 in. Tn = 0. 9 Fy. Astem = (0. 9 x 50)(0. 430 x 7. 62) = 147 k > 80 k (Rupture will not control) 72

Tee Flange Yielding and Rupture Shear Yielding of Flange: tf = 0. 715 in. Rn = 0. 9(0. 6 Fy)Agv = 0. 9 (0. 6 x 50) (2 x 8. 0 x 0. 715) = 309 k > 80 k 73

Tee Flange Yielding and Rupture Shear Rupture of Flange: tf = 0. 715 in. Rn = 0. 75(0. 6 Fu)Anv = 0. 75 (0. 6 x 65) (2) (8. 0– 2 x 0. 875) (0. 715) = 261 k > 80 k 74

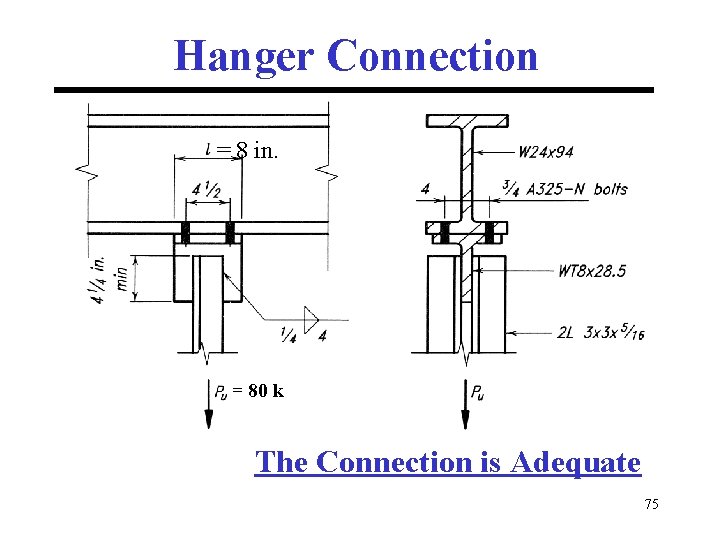
Hanger Connection = 8 in. = 80 k The Connection is Adequate 75